Система переменной массы

В механике система переменной массы — это совокупность материи которой , масса меняется со временем . Попытка применить второй закон движения Ньютона непосредственно к такой системе может сбить с толку. ^[1]^[2] Вместо этого зависимость массы m от времени можно рассчитать, переформулировав второй закон Ньютона и добавив член для учета импульса, переносимого массой, входящей или выходящей из системы. Общее уравнение движения переменной массы записывается как

\mathbf {F} _{\mathrm {ext} }+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v}  \over \mathrm {d} t}

где F _ext — результирующая внешняя сила, действующая на тело, v _rel — относительная скорость убегающей или приближающейся массы относительно центра масс тела, а v — скорость тела. ^[3] В астродинамике механикой ракет , термин vrel _и часто называют эффективной скоростью истечения обозначают ve _{, которая занимается} . ^[4]

Вывод

Существуют разные выводы уравнения движения системы переменной массы в зависимости от того, входит ли масса в тело или покидает его (другими словами, увеличивается или уменьшается масса движущегося тела соответственно). Для упрощения расчетов все тела рассматриваются как частицы . Также предполагается, что масса не способна применять внешние силы к телу за пределами событий аккреции/абляции.

Массовая аккреция

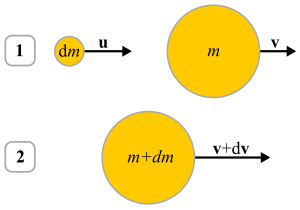
Следующий вывод относится к телу, которое набирает массу ( аккрецию ). Тело изменяющейся во времени массы m движется со скоростью v в начальный момент времени t . В этот же момент частица массы dm движется со скоростью u относительно земли. Начальный импульс можно записать как ^[5]

\mathbf {p} _{\mathrm {1} }=m\mathbf {v} +\mathbf {u} \mathrm {d} m

Теперь в момент времени t + d t пусть и основное тело, и частица срастаются в тело со скоростью v + d v . Таким образом, новый импульс системы можно записать как

\mathbf {p} _{\mathrm {2} }=(m+\mathrm {d} m)(\mathbf {v} +\mathrm {d} \mathbf {v} )=m\mathbf {v} +m\mathrm {d} \mathbf {v} +\mathbf {v} \mathrm {d} m+\mathrm {d} m\mathrm {d} \mathbf {v}

Поскольку d m d v является произведением двух малых величин, его можно игнорировать, то есть в течение d t импульс системы изменяется по

\mathrm {d} \mathbf {p} =\mathbf {p} _{\mathrm {2} }-\mathbf {p} _{\mathrm {1} }=(m\mathbf {v} +m\mathrm {d} \mathbf {v} +\mathbf {v} \mathrm {d} m)-(m\mathbf {v} +\mathbf {u} \mathrm {d} m)=m\mathrm {d} \mathbf {v} -(\mathbf {u} -\mathbf {v} )\mathrm {d} m

Следовательно, по второму закону Ньютона

\mathbf {F} _{\mathrm {ext} }={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {m\mathrm {d} \mathbf {v} -(\mathbf {u} -\mathbf {v} )\mathrm {d} m}{\mathrm {d} t}}=m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}-(\mathbf {u} -\mathbf {v} ){\frac {\mathrm {d} m}{\mathrm {d} t}}

Учитывая, что , обозначенная как v rel , это u-v — это скорость d m относительно m окончательное уравнение _можно записать как ^[6]

\mathbf {F} _{\mathrm {ext} }+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v}  \over \mathrm {d} t}

Массовая абляция/извлечение

В системе, где масса выбрасывается или удаляется из основного тела, результат немного другой. Пусть в момент времени t масса m движется со скоростью v , что означает, что начальный импульс системы равен

\mathbf {p} _{\mathrm {1} }=m\mathbf {v}

Предполагая, что u — скорость удаляемой массы d m относительно земли, в момент времени t + d t импульс системы становится

\mathbf {p} _{\mathrm {2} }=(m-\mathrm {d} m)(\mathbf {v} +\mathrm {d} \mathbf {v} )+\mathbf {u} \mathrm {d} m=m\mathbf {v} +m\mathrm {d} \mathbf {v} -\mathbf {v} \mathrm {d} m-\mathrm {d} m\mathrm {d} \mathbf {v} +\mathbf {u} \mathrm {d} m

где u - скорость выброшенной массы относительно земли, и она отрицательна, поскольку удаляемая масса движется в направлении, противоположном массе. Таким образом, в течение d t импульс системы меняется на

\mathrm {d} \mathbf {p} =\mathbf {p} _{\mathrm {2} }-\mathbf {p} _{\mathrm {1} }=(m\mathbf {v} +m\mathrm {d} \mathbf {v} -\mathrm {d} \mathbf {m} \mathrm {d} \mathbf {v} -\mathbf {v} \mathrm {d} m+\mathbf {u} \mathrm {d} m)-(m\mathbf {v} )=m\mathrm {d} \mathbf {v} +[\mathbf {u} -(\mathbf {v} +\mathrm {d} \mathbf {v} )]\mathrm {d} m

Относительная скорость v _rel аблированной массы относительно массы m записывается как

\mathbf {v} _{\mathrm {rel} }=\mathbf {u} -(\mathbf {v} +\mathrm {d} \mathbf {v} )

Следовательно, изменение импульса можно записать как

\mathrm {d} \mathbf {p} =m\mathrm {d} \mathbf {v} +\mathbf {v} _{\mathrm {rel} }\mathrm {d} m

Следовательно, по второму закону Ньютона

\mathbf {F} _{\mathrm {ext} }={\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}={\frac {m\mathrm {d} \mathbf {v} +\mathbf {v} _{\mathrm {rel} }\mathrm {d} m}{\mathrm {d} t}}=m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}

Следовательно, окончательное уравнение можно записать в виде

\mathbf {F} _{\mathrm {ext} }-\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} \mathbf {v}  \over \mathrm {d} t}

Формы

По определению ускорения , a = d v /d t поэтому уравнение движения системы переменной массы можно записать как

\mathbf {F} _{\mathrm {ext} }+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m\mathbf {a}

В телах, которые не рассматриваются как частицы, , ускорение центра _{a необходимо заменить на cm} масс системы , т.е.

\mathbf {F} _{\mathrm {ext} }+\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m\mathbf {a} _{\mathrm {cm} }

Часто силу тяги определяют как $\mathbf {F} _{\mathrm {thrust} }=\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}$ так что

\mathbf {F} _{\mathrm {ext} }+\mathbf {F} _{\mathrm {thrust} }=m\mathbf {a} _{\mathrm {cm} }

Эта форма показывает, что тело может иметь ускорение от тяги, даже если на него не действуют никакие внешние силы ( F _ext = 0). Наконец, обратите внимание, что если позволить F _net быть суммой F _ext и F _тяги , то уравнение вновь обретет обычную форму второго закона Ньютона:

\mathbf {F} _{\mathrm {net} }=m\mathbf {a} _{\mathrm {cm} }

Уравнение идеальной ракеты

Уравнение идеальной ракеты , или уравнение ракеты Циолковского , можно использовать для изучения движения транспортных средств, которые ведут себя как ракета (когда тело ускоряется, выбрасывая часть своей массы, топливо , с высокой скоростью). Его можно вывести из общего уравнения движения систем переменной массы следующим образом: при отсутствии внешних сил на тело ( F _ext = 0) уравнение движения системы переменной массы сводится к виду ^[2]

\mathbf {v} _{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}

Если предполагается, что скорость выброшенного топлива v _rel имеет направление, противоположное ускорению ракеты d v /d t , скалярный эквивалент этого уравнения можно записать как

-v_{\mathrm {rel} }{\frac {\mathrm {d} m}{\mathrm {d} t}}=m{\mathrm {d} v \over \mathrm {d} t}

из которого d t можно вычесть, чтобы получить

-v_{\mathrm {rel} }\mathrm {d} m=m\mathrm {d} v\,

Интегрирование путем разделения переменных дает

-v_{\mathrm {rel} }\int _{m_{0}}^{m_{1}}{\frac {\mathrm {d} m}{m}}=\int _{v_{0}}^{v_{1}}\mathrm {d} v

v_{\mathrm {rel} }\ln {\frac {m_{0}}{m_{1}}}=v_{1}-v_{0}

Переставляя и допуская Δ v = v ₁ - v ₀ , можно прийти к стандартной форме уравнения идеальной ракеты:

\Delta v=v_{\mathrm {rel} }\ln {\frac {m_{0}}{m_{1}}}

где m ₀ — начальная полная масса, включая топливо, m ₁ — конечная полная масса, v _rel — эффективная скорость выхлопа (часто обозначаемая как v _e ), а Δ v — максимальное изменение скорости транспортного средства (при отсутствии действуют внешние силы).

Ссылки

^ Клеппнер, Д .; Коленков, Р.Дж. (1978) [1973]. Введение в механику . Лондон: МакГроу-Хилл . стр. 133–139 . ISBN 0-07-035048-5 .
^ Jump up to: ^а ^б Басавараджу, Г; Гош, Дипин (1 февраля 1985 г.). Механика и термодинамика . Тата МакГроу-Хилл . стр. 162–165. ISBN 978-0-07-451537-2 .
^ Пластино, Анхель Р.; Муццио, Хуан К. (1992). «Об использовании и злоупотреблениях вторым законом Ньютона для задач с переменной массой» . Небесная механика и динамическая астрономия . 53 (3). Нидерланды: Издательство Kluwer Academic: 227–232. Бибкод : 1992CeMDA..53..227P . дои : 10.1007/BF00052611 . ISSN 0923-2958 . S2CID 122212239 . Проверено 30 декабря 2011 г.
^ Бенсон, Том. «Уравнение идеальной ракеты» . НАСА . Архивировано из оригинала 11 октября 2007 года . Проверено 30 декабря 2011 г.
^ Цветиканин, Л. (21 октября 1998 г.). Динамика машин переменной массы (1-е изд.). ЦРК Пресс . стр. 15–20. ISBN 978-90-5699-096-1 .
^ Джанколи, Дуглас К. (2008). Физика для ученых и инженеров . Том. 2 (4, иллюстрированное изд.). Пирсон Образование. стр. 236–238. ISBN 978-0-13-227359-6 .

[1] Клеппнер, Д .; Коленков, Р.Дж. (1978) [1973]. Введение в механику . Лондон: МакГроу-Хилл . стр. 133–139 . ISBN 0-07-035048-5 .

[Basavaraju-2] Jump up to: ^а ^б Басавараджу, Г; Гош, Дипин (1 февраля 1985 г.). Механика и термодинамика . Тата МакГроу-Хилл . стр. 162–165. ISBN 978-0-07-451537-2 .

[Plastino-3] Пластино, Анхель Р.; Муццио, Хуан К. (1992). «Об использовании и злоупотреблениях вторым законом Ньютона для задач с переменной массой» . Небесная механика и динамическая астрономия . 53 (3). Нидерланды: Издательство Kluwer Academic: 227–232. Бибкод : 1992CeMDA..53..227P . дои : 10.1007/BF00052611 . ISSN 0923-2958 . S2CID 122212239 . Проверено 30 декабря 2011 г.

[NASA-4] Бенсон, Том. «Уравнение идеальной ракеты» . НАСА . Архивировано из оригинала 11 октября 2007 года . Проверено 30 декабря 2011 г.

[Cveticanin-5] Цветиканин, Л. (21 октября 1998 г.). Динамика машин переменной массы (1-е изд.). ЦРК Пресс . стр. 15–20. ISBN 978-90-5699-096-1 .

[Giancoli-6] Джанколи, Дуглас К. (2008). Физика для ученых и инженеров . Том. 2 (4, иллюстрированное изд.). Пирсон Образование. стр. 236–238. ISBN 978-0-13-227359-6 .

[1]

[2]

[3]

[4]

[5]

[6]