Ультраграф C*-алгебры

В математике ультраграф C*-алгебра — это универсальная C*-алгебра, порожденная частичными изометриями набора гильбертовых пространств, построенных из ультраграфов. ^[1]^{стр. 6-7}. Эти C*-алгебры были созданы с целью одновременного обобщения классов графовых C*-алгебр и алгебр Экселя–Лаки, дающих единую основу для изучения этих объектов. ^[1] Это связано с тем, что каждый граф может быть закодирован как ультраграф, и аналогично каждый бесконечный граф, дающий алгебру Экселя-Лака, также может быть закодирован как ультраграф.

Определения

Ультраграфы

УЗИ ${\mathcal {G}}=(G^{0},{\mathcal {G}}^{1},r,s)$ состоит из множества вершин $G^{0}$ , набор ребер ${\mathcal {G}}^{1}$ , исходная карта $s:{\mathcal {G}}^{1}\to G^{0}$ и карта диапазона $r:{\mathcal {G}}^{1}\to P(G^{0})\setminus \{\emptyset \}$ получение значений из наборов мощности коллекции $P(G^{0})\setminus \{\emptyset \}$ непустых подмножеств множества вершин. Ориентированный граф — это частный случай ультраграфа, в котором диапазон каждого ребра представляет собой один элемент, а ультраграфы можно рассматривать как обобщенный ориентированный граф, в котором каждое ребро начинается в одной вершине и указывает на непустое подмножество вершин.

Пример

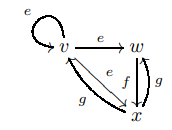
Ультраграфическая визуализация — Ультраграф $(\{v,w,x\},\{e,f,g\},s,r)$

Простой способ визуализировать ультраграф — рассмотреть ориентированный граф с набором помеченных вершин, где каждая метка соответствует подмножеству изображения элемента карты диапазонов. Например, задан ультраграф с вершинами и метками ребер.

${\mathcal {G}}^{0}=\{v,w,x\}$ , ${\mathcal {G}}^{1}=\{e,f,g\}$

с источником и картами диапазона

${\begin{matrix}s(e)=v&s(f)=w&s(g)=x\\r(e)=\{v,w,x\}&r(f)=\{x\}&r(g)=\{v,w\}\end{matrix}}$

можно представить как изображение справа.

Ультраграфические алгебры

Учитывая ультраграфию ${\mathcal {G}}=(G^{0},{\mathcal {G}}^{1},r,s)$ , мы определяем ${\mathcal {G}}^{0}$ быть наименьшим подмножеством $P(G^{0})$ содержащий одноэлементные наборы $\{\{v\}:v\in G^{0}\}$ , содержащий наборы диапазонов $\{r(e):e\in {\mathcal {G}}^{1}\}$ и замкнуты относительно пересечений, объединений и относительных дополнений. А Кунц-Кригер ${\mathcal {G}}$ -семья – это совокупность проекций $\{p_{A}:A\in {\mathcal {G}}^{0}\}$ вместе с набором частичных изометрий $\{s_{e}:e\in {\mathcal {G}}^{1}\}$ со взаимно ортогональными диапазонами, удовлетворяющими

$p_{\emptyset }$ , $p_{A}p_{B}=p_{A\cap B}$ , $p_{A}+p_{B}-p_{A\cap B}=p_{A\cup B}$ для всех $A\in {\mathcal {G}}^{0}$ ,
$s_{e}^{*}s_{e}=p_{r(e)}$ для всех $e\in {\mathcal {G}}^{1}$ ,
$p_{v}=\sum _{s(e)=v}s_{e}s_{e}^{*}$ в любое время $v\in G^{0}$ - это вершина, которая испускает конечное число ребер, и
$s_{e}s_{e}^{*}\leq p_{s(e)}$ для всех $e\in {\mathcal {G}}^{1}$ .

Ультраграф C*-алгебры $C^{*}({\mathcal {G}})$ — универсальная C*-алгебра, порожденная алгеброй Кунца–Кригера ${\mathcal {G}}$ -семья.

Характеристики

Любую графовую C*-алгебру можно рассматривать как алгебру ультраграфа, если просто рассматривать граф как частный случай ультраграфа и понимать, что ${\mathcal {G}}^{0}$ представляет собой совокупность всех конечных подмножеств $G^{0}$ и $p_{A}=\sum _{v\in A}p_{v}$ для каждого $A\in {\mathcal {G}}^{0}$ . Любая алгебра Экселя–Лака также является ультраграфом C*-алгеброй: если $A$ представляет собой бесконечную квадратную матрицу с набором индексов $I$ и записи в $\{0,1\}$ , можно определить ультраграф по формуле $G^{0}:=$ , $G^{1}:=I$ , $s(i)=i$ , и $r(i)=\{j\in I:A(i,j)=1\}$ . Можно показать, что $C^{*}({\mathcal {G}})$ изоморфна алгебре Экселя–Лаки ${\mathcal {O}}_{A}$ . ^[1]

Ультраграфные C*-алгебры являются полезными инструментами для изучения как графовых C*-алгебр, так и алгебр Экселя – Лака. Среди других преимуществ моделирование алгебры Экселя – Лака как ультраграфа C*-алгебры позволяет использовать ультраграф как инструмент для изучения связанных C*-алгебр, тем самым предоставляя возможность использовать методы теории графов, а не матричные методы. при изучении алгебры Экселя–Лаки. Ультраграф C*-алгебры использовались, чтобы показать, что каждая простая AF-алгебра изоморфна либо графу C*-алгебре, либо алгебре Экселя – Лака. ^[2] Они также использовались для доказательства того, что каждая AF-алгебра без (ненулевого) конечномерного фактора изоморфна алгебре Экселя – Лака. ^[2]

Хотя каждый из классов графовых C*-алгебр, алгебр Экселя–Лака и ультраграфических C*-алгебр содержит C*-алгебры, не изоморфные ни одной C*-алгебре в двух других классах, было показано, что эти три класса совпадают. к эквивалентности Морита . ^[3]

См. также

Примечания

^ Jump up to: ^а ^б ^с Единый подход к алгебрам Экселя–Лаки и C*-алгебрам, связанным с графами , Марк Томфорд, J. Теория операторов 50 (2003), вып. 2, 345–368.
^ Jump up to: ^а ^б Реализация AF-алгебр как алгебр-графиков, алгебр Экселя – Лака и алгебр-ультраграфов , Такеши Кацура, Эйдан Симс и Марк Томфорд, J. Funct. Анальный. 257 (2009), вып. 5, 1589–1620 гг.
^ Алгебры графов, алгебры Экселя – Лаки и алгебры ультраграфов совпадают с точностью до эквивалентности Мориты , Такеши Кацура, Пол Мьюли, Эйдан Симс и Марк Томфорд, Дж. Рейн Ангью. Математика. 640 (2010), 135–165.

[Tom-1] Jump up to: ^а ^б ^с Единый подход к алгебрам Экселя–Лаки и C*-алгебрам, связанным с графами , Марк Томфорд, J. Теория операторов 50 (2003), вып. 2, 345–368.

[KST-2] Jump up to: ^а ^б Реализация AF-алгебр как алгебр-графиков, алгебр Экселя – Лака и алгебр-ультраграфов , Такеши Кацура, Эйдан Симс и Марк Томфорд, J. Funct. Анальный. 257 (2009), вып. 5, 1589–1620 гг.

[3] Алгебры графов, алгебры Экселя – Лаки и алгебры ультраграфов совпадают с точностью до эквивалентности Мориты , Такеши Кацура, Пол Мьюли, Эйдан Симс и Марк Томфорд, Дж. Рейн Ангью. Математика. 640 (2010), 135–165.

[1]

[2]

[3]