Додекаэдрический купол
 | Эта статья в значительной степени или полностью опирается на один источник . ( апрель 2024 г. ) |
| Додекаэдрический купол | ||
|---|---|---|
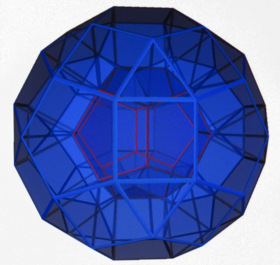 Диаграмма Шлегеля | ||
| Тип | Многогранный купол | |
| Символ Шлефли | {5,3} v рр{5,3} | |
| Клетки | 64 | 1 руб.{5,3}  1 {5,3}  30 {}×{3}  12 {}×{5}  20 {3,3}  |
| Лица | 194 | 80 треугольников 90 квадратов 24 пятиугольника |
| Края | 210 | |
| Вершины | 80 | |
| Двойной | ||
| Группа симметрии | [5,3,1], порядок 120 | |
| Характеристики | выпуклый , с правильным лицом | |
В 4-мерной геометрии додекаэдрический купол представляет собой полихорон, ограниченный ромбокосододекаэдром , параллельным додекаэдром , соединенным 30 треугольными призмами , 12 пятиугольными призмами и 20 тетраэдрами . [1]
Связанные многогранники
[ редактировать ]Додекаэдрический купол можно отрезать от укороченной 120-ячеечной ячейки на гиперплоскости , параллельной додекаэдрической ячейке. Купол можно увидеть в пятиугольной центрированной ортогональной проекции изрезанных 120 ячеек:
Ранцинированный, 120 ячеек 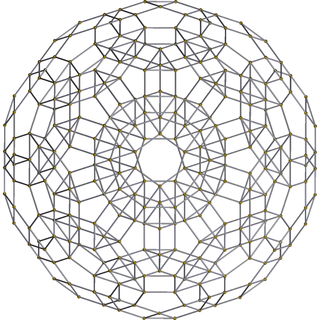 | Додекаэдр  (верх купола) |
Ромбикосидодекаэдр 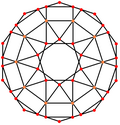 (основание купола) |
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Выпуклая сегментохора, доктор Ричард Клитцинг, Симметрия: культура и наука, Vol. 11, №№ 1-4, 139-181, 2000 (4,152 додекаэдр || ромбикосидодекаэдр)
Внешние ссылки
[ редактировать ] | Эта из 4-х многогранников статья незавершена . Вы можете помочь Википедии, расширив ее . |