Обобщенная география

В сложности вычислений теории обобщенная география является хорошо известной PSPACE-полной задачей.

Введение

География — детская игра , в которой игроки по очереди называют города из любой точки мира. Каждый выбранный город должен начинаться с той же буквы, которой заканчивалось предыдущее название города. Повтор не допускается. Игра начинается с произвольного стартового города и заканчивается, когда игрок проигрывает, потому что не может продолжить.

Графовая модель

Для визуализации игры можно построить ориентированный граф , узлами которого являются все города мира. Стрелка добавляется от узла N ₁ к узлу N ₂ тогда и только тогда, когда маркировка города N ₂ начинается с буквы, оканчивающей имя узла маркировки города N ₁ . Другими словами, мы рисуем стрелку от одного города к другому, если первый по правилам игры может вести ко второму. Каждое альтернативное ребро ориентированного графа соответствует каждому игроку (для игры с двумя игроками). Проигрывает тот игрок, который первым не сможет продлить путь. Иллюстрация игры (содержащая некоторые города Мичигана) показана на рисунке ниже.

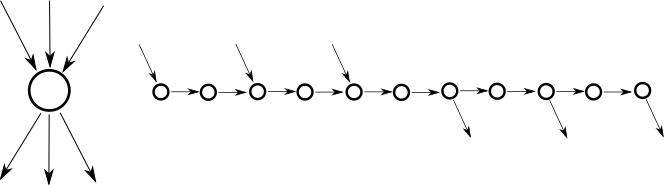
В игре по обобщенной географии (ОГ) мы заменяем граф названий городов произвольным ориентированным графом. Следующий график представляет собой пример обобщенной географической игры.

Игра в игру

Мы определяем P ₁ как игрока, двигающегося первым, и P ₂ как игрока, двигающегося вторым, и называем узлы от N ₁ до N _n . приведенном выше рисунке P1 _На следующую выигрышную стратегию: N1 _{указывает} на узлы N2 _имеет и N3 _только . Таким образом, P1 _{первый ход игрока} должен быть одним из этих двух вариантов. P1 _{поскольку} выбирает N2 _P1 (если выбирает _и N3 , _то P2 выберет _это N9 , _P1 единственный вариант, проиграет ₎ . Следующий P ₂ выбирает N ₄ , потому что это единственный оставшийся выбор. P ₁ теперь выбирает N ₅ , а P ₂ впоследствии выбирает N ₃ или N ₇ . Независимо от игрока ₂ не остается выбора , выбора , игрок ₁ выбирает номер ₉ , а у игрока ₂ и он проигрывает игру.

Вычислительная сложность

Задача определения того, какой игрок имеет выигрышную стратегию в игре с обобщенной географией, является PSPACE-полной .

Обобщенная география находится в PSPACE.

Пусть GG знак равно { ⟨ G , б ⟩ | P ₁ имеет выигрышную стратегию для игры в обобщенную географию, в которую играют на графе G, начиная с узла b }; Чтобы показать, что GG ∈ PSPACE , мы представляем рекурсивный алгоритм в полиномиальном пространстве, определяющий, какой игрок имеет выигрышную стратегию. Учитывая экземпляр GG, ⟨ G , n _start ⟩, где G — ориентированный граф, а n _start — назначенный начальный узел, алгоритм M действует следующим образом:

На M (⟨ G , n _старт ⟩):

Измерьте степень выхода узла n _start . Если эта степень равна 0, то верните отклонить , поскольку для первого игрока нет доступных ходов.
Создайте список всех узлов, достижимых из n, _{начиная} с одного ребра: n ₁ , n ₂ , ..., n _i .
Удалите n _start и все соединенные с ним ребра из G, чтобы образовать G ₁ .
Для каждого узла n _j в списке n ₁ , ..., n _i вызовите M (⟨ G ₁ , n _j ⟩).
Если все эти вызовы возвращают Accept , то независимо от того, какое решение примет P ₁ , у P ₂ есть стратегия победы, поэтому верните Reject . противном случае (если один из вызовов возвращает отказ ) P1 _у есть выбор, который отклонит любые успешные стратегии для P2 _В , поэтому верните Accept .

Алгоритм М явно решает ГГ. Это PSPACE , потому что единственное неочевидное полиномиальное рабочее пространство находится в стеке рекурсии. Пространство, занимаемое стеком рекурсии, является полиномиальным, поскольку каждый уровень рекурсии добавляет в стек один узел, и существует не более n уровней, где n — количество узлов в G . По сути, это эквивалентно поиску в глубину .

Обобщенная география сложна для PSPACE.

Следующее доказательство принадлежит Дэвиду Лихтенштейну и Майклу Сипсеру. ^[1]

Чтобы установить PSPACE-трудность GG, мы можем свести задачу FORMULA-GAME (которая, как известно, PSPACE-трудна ) к GG за полиномиальное время ( P ). Короче говоря, пример задачи ФОРМУЛА-ИГРА состоит из количественной булевой формулы φ = ∃ x ₁ ∀ x ₂ ∃ x ₃ ... Qx _k (ψ), где Q равно либо ∃, либо ∀. игре участвуют два игрока, и _В Pe , _{которые} поочередно выбирают значения для последовательных xi _. Pa P _e выигрывает игру, если формула ψ оказывается истинной , а P _a выигрывает, если ψ оказывается ложной . Предполагается, что формула ψ находится в конъюнктивной нормальной форме .

В этом доказательстве мы предполагаем, что список кванторов начинается и заканчивается экзистенциальным квалификатором ∃ для простоты. Обратите внимание, что любое выражение можно преобразовать в эту форму, добавив фиктивные переменные, которых нет в ψ.

Построив граф G, подобный показанному выше, мы покажем, что любой пример ФОРМУЛЫ-ИГРЫ можно свести к экземпляру Обобщенной географии, где оптимальная стратегия для P ₁ эквивалентна стратегии P _e , а оптимальная стратегия для P ₂ эквивалентен P _a .

Левая вертикальная цепочка узлов предназначена для имитации процедуры выбора значений переменных в ФОРМУЛЕ-ИГРЕ. Каждая ромбовидная структура соответствует количественной переменной. Игроки по очереди выбирают пути в каждом узле ветвления. что первый квантор будет экзистенциальным, P ₁ идет первым, выбирая левый узел, если x ₁ истинно Поскольку мы предполагали , , и правый узел, x ₁ ложно если . Затем каждый игрок должен совершить вынужденный ход, а затем P ₂ выбирает значение x ₂ . Эти чередующиеся задания продолжаются с левой стороны. После того, как оба игрока переберут все ромбы, снова наступает очередь P ₁ , поскольку мы предположили, что последний квантор является экзистенциальным. У P ₁ нет другого выбора, кроме как следовать по пути к правой части графа. Затем наступает P2 _{очередь игрока} сделать ход.

Когда ход игры достигает правой части графика, это похоже на конец игры в игре по формуле. Напомним, что в игре по формуле P _e выигрывает, если ψ истинно , а P _a выигрывает, если ψ ложно . Правая часть графика гарантирует, что выиграет _P1 тогда и только тогда, когда Pe _{выиграет} , и что P2 _когда выиграет тогда и только тогда, Pa _{выиграет} .

Сначала мы покажем, что P ₂ всегда выигрывает, когда выигрывает P _a . Если P _a выигрывает, ψ ложно . Если ψ ложно , существует неудовлетворительное условие. P ₂ выберет неудовлетворительное предложение для победы. Затем, когда наступит очередь P1 _, он должен выбрать литерал в предложении, P2 _{выбранном} . Поскольку все литералы в предложении имеют значение false , они не соединяются с ранее посещенными узлами в левой вертикальной цепочке. Это позволяет P ₂ проследить соединение с соответствующим узлом в ромбе левой цепи и выбрать его. Однако P1 _. теперь не может выбрать ни один соседний узел и проигрывает

Теперь мы покажем, что P ₁ всегда выигрывает, когда выигрывает P _e . Если P _e выигрывает , ψ истинно . Если ψ истинно , каждое предложение в правой части графика содержит истинный литерал. P ₂ может выбрать любое предложение. Затем P1 _. литерал верный выбирает А поскольку это правда , соседний с ним узел в левом вертикальном узле уже выбран, поэтому P2 _игроку нечего делать и он проигрывает.

Плоская обобщенная география является PSPACE-полной.

Обобщенная география является PSPACE-полной, даже если воспроизводить ее на плоских графах . Следующее доказательство взято из теоремы 3. ^[1]

Поскольку планарный GG является частным случаем GG, а GG находится в PSPACE, то планарный GG находится в PSPACE. Осталось показать, что планарная GG PSPACE-трудна. Это можно доказать, показав, как преобразовать произвольный граф в планарный граф так, чтобы игра GG, сыгранная на этом графе, имела тот же результат, что и на исходном графе.

Для этого необходимо лишь исключить все пересечения ребер исходного графа. Мы рисуем граф так, чтобы никакие три ребра не пересекались в одной точке и ни одна пара пересекающихся ребер не могла использоваться одновременно в одной и той же игре. В общем случае это невозможно, но всегда возможно для графа, построенного на основе экземпляра FORMULA-GAME; например, мы могли бы иметь только ребра вершин предложения, участвующие в пересечениях. Теперь заменим каждое пересечение такой конструкцией:

Результатом является плоский граф, и тот же игрок может добиться победы, как и в исходном графе: если игрок решает двигаться «вверх» от V в преобразованной игре, то оба игрока должны продолжать двигаться «вверх» к W, иначе они проиграют. немедленно. Таким образом, движение «вверх» от V в преобразованной игре имитирует ход V → W в исходной игре. Если V→W — выигрышный ход, то движение «вверх» от V в преобразованной игре также является выигрышным ходом, и наоборот.

Таким образом, игра ГГ на преобразованном графе будет иметь тот же результат, что и на исходном графе. Это преобразование требует времени, кратного числу пересечений ребер в исходном графе, поэтому оно занимает полиномиальное время.

Таким образом, планарная GG является PSPACE-полной.

Плоский двудольный граф с максимальной степенью 3

Игра GG на плоских двудольных графах с максимальной степенью 3 по-прежнему остается PSPACE-полной за счет замены вершин степени выше 3 цепочкой вершин степени не выше 3. Доказательство имеется. ^[1] и использует следующую конструкцию:

Если один игрок использует любой из входов в это сооружение, другой игрок выбирает, какой выход будет использоваться. Кроме того, конструкцию можно пройти только один раз, поскольку центральная вершина посещается всегда. Следовательно, эта конструкция эквивалентна исходной вершине.

Краевая география

Вариант ГГ называется географией края , где после каждого хода край, который прошел игрок, стирается. В этом отличие от оригинальной GG, где после каждого хода вершина, на которой раньше находился игрок, стирается. С этой точки зрения исходную GG можно назвать Vertex Geography .

География границ является PSPACE-полной. Это можно доказать, используя ту же конструкцию, которая использовалась для географии вершин. ^[2]

Неориентированная география

Можно также рассмотреть возможность сыграть в любую географическую игру на неориентированном графе (то есть, ребра можно проходить в обоих направлениях). Френкель, Шайнерман и Ульман ^[3] покажите, что неориентированная география вершин может быть решена за полиномиальное время, тогда как неориентированная география ребер является PSPACE-полной даже для планарных графов с максимальной степенью 3. Если граф двудольный, то ненаправленная география ребер разрешима за полиномиальное время.

Последствия

Учитывая, что GG является PSPACE-полным , не существует алгоритма с полиномиальным временем для оптимальной игры в GG, если только P = PSPACE . Однако доказать сложность других игр может оказаться не так просто, поскольку некоторые игры (например, шахматы ) содержат конечное число игровых позиций, что затрудняет (или делает невозможным) формулирование отображения для PSPACE-полной задачи. Несмотря на это, сложность некоторых игр все же можно проанализировать путем обобщения (например, для доски n × n ). См. ссылки на доказательство обобщенного Go как следствие доказательства полноты GG.

Ссылки

^ Перейти обратно: ^а ^б ^с Лихтенштейн, Дэвид; Сипсер, Майкл (апрель 1980 г.). «Go — это сложно в полиномиальном пространстве» (PDF) . Журнал АКМ . 27 (2): 393–401. дои : 10.1145/322186.322201 .
^ Шефер, Томас Дж. (1978). «О сложности некоторых игр двух лиц с совершенной информацией». Журнал компьютерных и системных наук . 16 (2): 185–225. дои : 10.1016/0022-0000(78)90045-4 .
^ Френкель, Авиезри; Шайнерман, Эдвард; Ульман, Дэниел (1993). «Ненаправленная география края». Теоретическая информатика . 112 (2): 371–381. дои : 10.1016/0304-3975(93)90026-п .

Майкл Сипсер, Введение в теорию вычислений , PWS, 1997.

[go-1] Перейти обратно: ^а ^б ^с Лихтенштейн, Дэвид; Сипсер, Майкл (апрель 1980 г.). «Go — это сложно в полиномиальном пространстве» (PDF) . Журнал АКМ . 27 (2): 393–401. дои : 10.1145/322186.322201 .

[2] Шефер, Томас Дж. (1978). «О сложности некоторых игр двух лиц с совершенной информацией». Журнал компьютерных и системных наук . 16 (2): 185–225. дои : 10.1016/0022-0000(78)90045-4 .

[3] Френкель, Авиезри; Шайнерман, Эдвард; Ульман, Дэниел (1993). «Ненаправленная география края». Теоретическая информатика . 112 (2): 371–381. дои : 10.1016/0304-3975(93)90026-п .

[1]

[2]

[3]