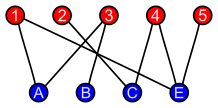
Двудольный граф

Пример двудольного графа без циклов

Полный двудольный граф с m = 5 и n = 3

Граф Хивуда двудольный.

В математической области теории графов ( двудольный граф или биграф ) — это граф которого , вершины можно разделить на два непересекающихся и независимых множества. $U$ и $V$, то есть каждое ребро соединяет вершину в $U$ одному в $V$. Наборы вершин $U$ и $V$ обычно называют частями графа. нечетной длины Эквивалентно, двудольный граф — это граф, который не содержит циклов .

Два набора $U$ и $V$ можно рассматривать как раскраску графа в два цвета: если раскрасить все узлы в $U$ синий, и все узлы в $V$ красный, каждое ребро имеет концы разного цвета, как это требуется в задаче о раскраске графа. Напротив, в случае недвудольного графа, такого как треугольник , такая раскраска невозможна : после того, как один узел окрашен в синий цвет, а другой в красный, третья вершина треугольника соединяется с вершинами обоих цветов, не позволяя ей присваивается любой цвет.

Часто пишут $G=(U,V,E)$ для обозначения двудольного графа, разбиение которого состоит из частей $U$ и $V$, с $E$ обозначающие ребра графа. Если двудольный граф несвязен , он может иметь более одного двудольного графа; в этом случае $(U,V,E)$ Обозначение полезно при указании одного конкретного бираздела, который может иметь значение в приложении. Если $|U|=|V|$, то есть, если два подмножества имеют одинаковую мощность , то $G$ называется сбалансированным двудольным графом. Если все вершины на одной стороне двудольного деления имеют одинаковую степень , то $G$ называется бирегулярным .

Примеры

При моделировании отношений между двумя разными классами объектов очень часто естественным образом возникают двудольные графы. Например, граф футболистов и клубов с перевесом между игроком и клубом, если игрок играл за этот клуб, является естественным примером сети филиалов , типа двудольного графа, используемого в анализе социальных сетей .

Другой пример естественного появления двудольных графов — это ( NP-полная ) задача оптимизации железных дорог, в которой входными данными является расписание поездов и их остановок, а цель — найти как можно меньший набор железнодорожных станций, чтобы каждый поезд посещает хотя бы одну из выбранных станций. Эту проблему можно смоделировать как проблему доминирующего множества в двудольном графе, который имеет вершину для каждого поезда и каждой станции и ребро для каждой пары станций и поезда, который останавливается на этой станции.

Третий пример относится к академической области нумизматики. Древние монеты изготавливаются с использованием двух положительных оттисков дизайна (аверса и реверса). Таблицы, которые нумизматы создают для представления производства монет, представляют собой двудольные графики.

Более абстрактные примеры включают следующее:

• Каждое дерево двудольное.
• Графы циклов с четным числом вершин являются двудольными.
• Любой планарный граф которого , все грани имеют четную длину, является двудольным. Особыми случаями этого являются сетчатые графы и квадратные графы , в которых каждая внутренняя грань состоит из 4 ребер, а каждая внутренняя вершина имеет четырех или более соседей.
• Полный двудольный граф на m и n вершинах, обозначаемый K _n,m, является двудольным графом $G=(U,V,E)$, где U и V — непересекающиеся множества размера m и n соответственно, а E соединяет каждую вершину в U со всеми вершинами в V . Отсюда следует, что K _m,n имеет mn ребер. С полными двудольными графами тесно связаны коронные графы , образованные из полных двудольных графов путем удаления ребер идеального паросочетания .
• Графы гиперкубов , частичные кубы и медианные графы являются двудольными. В этих графах вершины могут быть помечены битовыми векторами таким образом, что две вершины являются смежными тогда и только тогда, когда соответствующие битовые векторы различаются в одной позиции. Двуразделение может быть образовано путем отделения вершин, битвекторы которых имеют четное число единиц, от вершин с нечетным числом единиц. Деревья и квадратные графы образуют примеры медианных графов, и каждый медианный граф представляет собой частичный куб.

Характеристики

Характеристика

Двудольные графы можно охарактеризовать несколькими различными способами:

• Неориентированный граф является двудольным тогда и только тогда, когда он не содержит нечетного цикла .
• Граф является двудольным тогда и только тогда, когда он раскрашивается в 2 цвета (т. е. его хроматическое число меньше или равно 2).
• Граф является двудольным тогда и только тогда, когда каждое ребро принадлежит нечетному числу связей — минимальному подмножеству ребер, удаление которых увеличивает количество компонентов графа.
• Граф является двудольным тогда и только тогда, когда спектр графа симметричен.

Теорема Кенига и совершенные графы

В двудольных графах размер минимального покрытия вершин равен размеру максимального паросочетания ; это теорема Кенига . Альтернативная и эквивалентная форма этой теоремы состоит в том, что размер максимального независимого множества плюс размер максимального паросочетания равен числу вершин. В любом графе без изолированных вершин размер минимального реберного покрытия плюс размер максимального паросочетания равны числу вершин. Объединение этого равенства с теоремой Кенига приводит к тому, что в двудольных графах размер минимального покрытия ребер равен размеру максимального независимого множества, а размер минимального покрытия ребер плюс размер минимального покрытия вершин. равно числу вершин.

Другой класс связанных результатов касается идеальных графов : каждый двудольный граф, дополнение каждого двудольного графа, линейный граф каждого двудольного графа и дополнение линейного графа каждого двудольного графа совершенны. Совершенство двудольных графов легко увидеть (их хроматическое число равно двум, а максимальный размер клики также равен двум), но совершенство дополнений двудольных графов менее тривиально и является еще одним повторением теоремы Кенига. Это был один из результатов, который мотивировал первоначальное определение идеальных графов. Совершенство дополнений к линейным графам совершенных графов — это еще одна формулировка теоремы Кенига, а совершенство самих линейных графов — это повторение более ранней теоремы Кенига о том, что каждый двудольный граф имеет раскраску ребер с использованием числа цветов, равного его максимальная степень.

Согласно сильной теореме о совершенном графе , совершенные графы имеют запрещенную характеристику графа , аналогичную характеристике двудольных графов: граф является двудольным тогда и только тогда, когда он не имеет нечетного цикла в качестве подграфа, и граф совершенен тогда и только тогда, когда он имеет нет нечетного цикла или его дополнения как индуцированного подграфа . Двудольные графы, линейные графы двудольных графов и их дополнения образуют четыре из пяти основных классов совершенных графов, используемых при доказательстве сильной теоремы о совершенных графах. Отсюда следует, что любой подграф двудольного графа также является двудольным, поскольку в нем не может быть нечетного цикла.

Степень

Для вершины число соседних вершин называется степенью вершины и обозначается $\deg(v)$. Формула суммы степеней для двудольного графа гласит, что

$\sum _{v\in V}\deg(v)=\sum _{u\in U}\deg(u)=|E|\,.$

Последовательность степеней двудольного графа — это пара списков, каждый из которых содержит степени двух частей. $U$ и $V$. Например, полный двудольный граф K _3,5 имеет последовательность степеней $(5,5,5),(3,3,3,3,3)$. Изоморфные двудольные графы имеют одинаковую последовательность степеней. Однако последовательность степеней, как правило, не идентифицирует однозначно двудольный граф; в некоторых случаях неизоморфные двудольные графы могут иметь одинаковую последовательность степеней.

Проблема двудольной реализации — это проблема поиска простого двудольного графа, последовательность степеней которого представляет собой два заданных списка натуральных чисел. (Конечные нули можно игнорировать, поскольку они тривиально реализуются путем добавления соответствующего количества изолированных вершин к орграфу.)

Связь с гиперграфами и ориентированными графами

Матрица двусмежности двудольного графа $(U,V,E)$ представляет собой (0,1) матрицу размера $|U|\times |V|$ который имеет единицу для каждой пары соседних вершин и ноль для несмежных вершин. Матрицы бисмежности могут использоваться для описания эквивалентности между двудольными графами, гиперграфами и ориентированными графами.

Гиперграф — это комбинаторная структура, которая, как и неориентированный граф, имеет вершины и ребра, но в которой ребра могут представлять собой произвольные наборы вершин, а не иметь ровно две конечные точки. Двудольный граф $(U,V,E)$ может использоваться для моделирования гиперграфа, в котором U — это множество вершин гиперграфа, V — это множество гиперребер, а E содержит ребро от вершины гиперграфа v до ребра гиперграфа e точно тогда, когда v является одной из конечных точек е . При этом соответствии матрицы двудольных графов являются в точности матрицами инцидентности соответствующих гиперграфов. Как частный случай этого соответствия между двудольными графами и гиперграфами, любой мультиграф (граф, в котором может быть два или более ребер между одними и теми же двумя вершинами) может интерпретироваться как гиперграф, в котором некоторые гиперребра имеют равные наборы конечных точек, и представлен двудольным графом, не имеющим кратных смежностей и в котором все вершины на одной стороне двудольного графа имеют степень два.

Подобная реинтерпретация матриц смежности может быть использована, чтобы показать взаимно однозначное соответствие между ориентированными графами (на заданном количестве помеченных вершин, допускающих самоциклы) и сбалансированными двудольными графами с одинаковым количеством вершин по обе стороны от двуразделение. Ибо матрицей смежности ориентированного графа с n вершинами может быть любая (0,1) матрица размера $n\times n$, которую затем можно интерпретировать как матрицу смежности двудольного графа с n вершинами на каждой стороне его двудольного деления. В этой конструкции двудольный граф представляет собой двудольное двойное покрытие ориентированного графа.

Алгоритмы

Тестирование двусторонности

Можно проверить, является ли граф двудольным, и вернуть либо двухцветный цикл (если он двудольный), либо нечетный цикл (если это не так) за линейное время , используя поиск в глубину . Основная идея состоит в том, чтобы присвоить каждой вершине цвет, который отличается от цвета ее родителя в лесу поиска в глубину, назначая цвета при предварительном обходе леса поиска в глубину. Это обязательно обеспечит двухцветную раскраску охватывающего леса, состоящего из ребер, соединяющих вершины с их родителями, но может неправильно раскрасить некоторые нелесные ребра. В лесу поиска в глубину одна из двух конечных точек каждого нелесного ребра является предком другой конечной точки, и когда поиск в глубину обнаруживает ребро этого типа, он должен проверить, что эти две вершины имеют разные цвета. Если это не так, то путь в лесу от предка к потомку вместе с обесцвеченным ребром образуют нечетный цикл, который возвращается из алгоритма вместе с результатом, что граф не является двудольным. Однако если алгоритм завершается, не обнаружив нечетного цикла этого типа, то каждое ребро должно быть правильно раскрашено, и алгоритм возвращает раскраску вместе с результатом, что граф является двудольным.

Альтернативно, аналогичная процедура может использоваться с поиском в ширину вместо поиска в глубину. Опять же, каждому узлу присваивается цвет, противоположный цвету его родителя в лесу поиска, в порядке ширины. Если, когда вершина окрашена, существует ребро, соединяющее ее с ранее окрашенной вершиной того же цвета, то это ребро вместе с путями в лесу поиска в ширину, соединяющими две его конечные точки с их наименьшим общим предком, образует странный цикл. Если алгоритм завершается, не обнаружив таким образом нечетного цикла, то он, должно быть, нашел правильную раскраску и может с уверенностью заключить, что граф двудольный.

Для пересечений графов $n$ отрезки линий или другие простые фигуры на евклидовой плоскости , можно проверить, является ли график двудольным, и вернуть либо двухцветный, либо нечетный цикл во времени $O(n\log n)$, хотя сам график может иметь до $O\left(n^{2}\right)$ края.

Трансверсализация нечетного цикла

Основная статья: Трансверсализация нечетного цикла

Граф с нечетной трансверсалью цикла размером 2: удаление двух синих нижних вершин оставляет двудольный граф.

Трансверсализация нечетного цикла — это NP-полная алгоритмическая задача, которая спрашивает для данного графа G = ( V , E ) и числа k , существует ли набор из k вершин, удаление которых из G приведет к тому, что результирующий граф станет двудольным. Проблема решается с фиксированными параметрами , что означает, что существует алгоритм, время работы которого может быть ограничено полиномиальной функцией размера графа, умноженной на большую функцию от k . Название трансверсальная нечетного цикла происходит от того факта, что граф является двудольным тогда и только тогда, когда в нем нет нечетных циклов . Следовательно, чтобы удалить вершины из графа и получить двудольный граф, нужно «попасть во все нечетные циклы» или найти так называемое трансверсальное множество нечетных циклов. На иллюстрации каждый нечетный цикл в графе содержит синие (самые нижние) вершины, поэтому удаление этих вершин уничтожает все нечетные циклы и оставляет двудольный граф.

Проблема раздвоения ребер — это алгоритмическая проблема удаления как можно меньшего количества ребер, чтобы сделать граф двудольным, а также важная проблема в алгоритмике модификации графов. Эта проблема также решается с фиксированными параметрами и может быть решена со временем. ${\textstyle O\left(2^{k}m^{2}\right)}$, где k — количество ребер, которые нужно удалить, а m — количество ребер во входном графе.

Соответствие

Основная статья: Сопоставление (теория графов)

Паросочетание в графе — это подмножество его ребер, никакие два из которых не имеют общей конечной точки. Алгоритмы с полиномиальным временем известны для решения многих алгоритмических задач о сопоставлениях, включая максимальное сопоставление (поиск сопоставления, которое использует как можно больше ребер), сопоставление с максимальным весом и стабильный брак . Во многих случаях задачи сопоставления проще решать на двудольных графах, чем на недвудольных. и многие алгоритмы сопоставления, такие как алгоритм Хопкрофта – Карпа для сопоставления максимальной мощности. корректно работают только на двусторонних входах.

В качестве простого примера предположим, что набор $P$ людей все ищут работу из набора $J$ рабочих мест, причем не все люди подходят для всех должностей. Эту ситуацию можно смоделировать как двудольный граф. $(P,J,E)$ где край соединяет каждого соискателя работы с каждой подходящей работой. Идеальное соответствие описывает способ одновременного удовлетворения всех соискателей и заполнения всех вакансий; Теорема Холла о браке дает характеристику двудольных графов, допускающих идеальные паросочетания. Национальная программа подбора резидентов применяет методы сопоставления графов для решения этой проблемы для американских студентов-медиков , ищущих работу, и для работы в больницах .

Разложение Далмаджа – Мендельсона — это структурное разложение двудольных графов, которое полезно для поиска максимальных паросочетаний.

Дополнительные приложения

Двудольные графы широко используются в современной теории кодирования , особенно для декодирования кодовых слов, полученных из канала. Факторные графы и графы Таннера являются примерами этого. Граф Таннера — это двудольный граф, в котором вершины на одной стороне двудольного деления представляют собой цифры кодового слова, а вершины на другой стороне представляют собой комбинации цифр, сумма которых, как ожидается, без ошибок будет равна нулю в кодовом слове. Факторный граф — это тесно связанная сеть убеждений, используемая для вероятностного декодирования LDPC и турбокодов .

В информатике сеть Петри — это инструмент математического моделирования, используемый при анализе и моделировании параллельных систем. Система моделируется как двудольный ориентированный граф с двумя наборами узлов: набором узлов «места», которые содержат ресурсы, и набором узлов «событий», которые генерируют и/или потребляют ресурсы. Существуют дополнительные ограничения на узлы и ребра, ограничивающие поведение системы. Сети Петри используют свойства двудольных ориентированных графов и другие свойства, позволяющие математически доказывать поведение систем, а также позволяют легко реализовать моделирование системы.

В проективной геометрии графы Леви представляют собой форму двудольного графа, используемого для моделирования взаимодействий между точками и линиями в конфигурации . В соответствии с геометрическим свойством точек и линий, согласно которому каждые две прямые пересекаются не более чем в одной точке и каждые две точки соединяются одной прямой, графы Леви обязательно не содержат циклов длины четыре, поэтому их обхват должен быть шесть или более . .

См. также

• Двудольная размерность — минимальное количество полных двудольных графов, объединение которых является данным графом.
• Двудольное двойное покрытие — способ преобразования любого графа в двудольный путем удвоения его вершин.
• Двудольный гиперграф , обобщение двудольности на гиперграфы .
• Двудольный матроид — класс матроидов, включающий графические матроиды двудольных графов.
• Проекция двудольной сети — метод взвешивания для сжатия информации о двудольных сетях.
• Выпуклый двудольный граф — двудольный граф, вершины которого можно упорядочить так, чтобы окрестности вершин были смежными.
• Многодольный граф , обобщение двудольных графов на более чем два подмножества вершин.
• Граф четности , обобщение двудольных графов, в котором каждые два индуцированных пути между одними и теми же двумя точками имеют одинаковую четность.
• Квазидвудольный граф , разновидность задачи о дереве Штейнера, в которой терминалы образуют независимый набор, что позволяет использовать алгоритмы аппроксимации, обобщающие алгоритмы для двудольных графов.
• Разделенный граф — граф, вершины которого можно разделить на два подмножества, одно из которых является независимым, а другое — кликой.
• Задача Заранкевича о максимальном числе ребер в двудольном графе с запрещенными подграфами

Внешние ссылки

• «Граф двудольный» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Информационная система по классам графов и их включениям : двудольный граф
• Вайсштейн, Эрик В. , «Двудольный граф» , MathWorld
• Двудольные графы в системной биологии и медицине