Икосаэдрическая пирамида
| Икосаэдрическая пирамида | ||
|---|---|---|
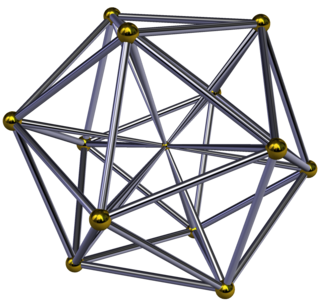 Диаграмма Шлегеля | ||
| Тип | Многогранная пирамида | |
| Символ Шлефли | ( ) ∨ {3,5} | |
| Клетки | 21 | 1 {3,5}  20 ( ) ∨ {3}  |
| Лица | 50 | 20+30 {3} |
| Края | 12+30 | |
| Вершины | 13 | |
| Двойной | Додекаэдрическая пирамида | |
| Группа симметрии | H 3 , [5,3,1], порядок 120 | |
| Характеристики | выпуклый , правильные ячейки, слепой многогранник | |
Икосаэдрическая пирамида представляет собой четырехмерный выпуклый многогранник , ограниченный одним икосаэдром в качестве основания и 20 треугольными ячейками пирамиды , которые сходятся на вершине. Поскольку радиус описанной окружности икосаэдра меньше длины его ребра, [1] тетраэдрические пирамиды могут быть выполнены с правильными гранями.
Имея все правильные ячейки, это Слепой многогранник . Две копии можно дополнить, чтобы получилась икосаэдральная бипирамида , которая также является слепым многогранником.
Обычный 600-ячеечный объект имеет икосаэдрические пирамиды вокруг каждой вершины.
Двойственной икосаэдрической пирамиде является додекаэдрическая пирамида , рассматриваемая как додекаэдрическое основание, и 12 правильных пятиугольных пирамид, встречающихся на вершине.
Конфигурация
[ редактировать ]В матрице конфигурации показаны все счетчики инцидентов между элементами. [2]
| k -грани | ж к | ж 0 | ж 1 | ff2 | f 3 | к -верс | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| ( ) | ж 0 | 1 | * | 12 | 0 | 30 | 0 | 20 | 0 | {3,5} |
| ( ) | * | 12 | 1 | 5 | 5 | 5 | 5 | 1 | {5}∨( ) | |
| ( )∨( ) | ж 1 | 1 | 1 | 12 | * | 5 | 0 | 5 | 0 | {5} |
| { } | 0 | 2 | * | 30 | 1 | 2 | 2 | 1 | { }∨( ) | |
| { }∨( ) | ff2 | 1 | 2 | 2 | 1 | 30 | * | 2 | 0 | { } |
| {3} | 0 | 3 | 0 | 3 | * | 20 | 1 | 1 | ( )∨( ) | |
| {3}∨( ) | f 3 | 1 | 3 | 3 | 3 | 3 | 1 | 20 | * | ( ) |
| {3,5} | 0 | 12 | 0 | 30 | 0 | 20 | * | 1 | ( ) | |
Ссылки
[ редактировать ]- ^ Клитцинг, Ричард. «3D выпуклые однородные многогранники х3о5о — айк» . , радиус окружности sqrt[(5+sqrt(5))/8 = 0,951057
- ^ Клитцинг, Ричард. «икепи» .
Внешние ссылки
[ редактировать ]- Ольшевский, Георгий. «Пирамида» . Глоссарий по гиперпространству . Архивировано из оригинала 4 февраля 2007 года.
- Клитцинг, Ричард. «4D Сегментотопы» .
- Клитцинг, Ричард. «Сегментотоп икепы, К-4,84» .
- Ричард Клитцинг, Осесимметричные грани однородных многогранников
- Икосаэдрическая пирамида
 | Эта из 4-х многогранников статья незавершена . Вы можете помочь Википедии, расширив ее . |