Сумматор с переносом вперед
Эта статья нуждается в дополнительных цитатах для проверки . ( август 2020 г. ) |
| Часть серии о | |||||||
| Арифметико-логические схемы | |||||||
|---|---|---|---|---|---|---|---|
| Быстрая навигация | |||||||
|
Теория |
|||||||
|
Компоненты
|
|||||||
|
Категории |
|||||||
|
См. также |
|||||||
Сумматор с упреждающим переносом ( CLA ) или быстрый сумматор — это тип электронного сумматора, используемого в цифровой логике. Сумматор с прогнозом переноса повышает скорость за счет сокращения времени, необходимого для определения битов переноса. Его можно противопоставить более простому, но обычно более медленному сумматору с пульсирующим переносом (RCA), в котором бит переноса вычисляется вместе с битом суммы, и каждый этап должен ждать, пока не будет вычислен предыдущий бит переноса, чтобы начать вычисление своего собственного. бит суммы и бит переноса. Сумматор с просмотром переноса вычисляет один или несколько битов переноса перед суммой, что сокращает время ожидания для вычисления результата старших битов сумматора.
Уже в середине 1800-х годов Чарльз Бэббидж осознал снижение производительности, вызванное пульсирующим переносом, используемым в его разностной машине , и впоследствии разработал механизмы упреждения переноса для своей так и не созданной аналитической машины . [1] [2] Считается, что Конрад Цузе реализовал первый сумматор с упреждающим переносом в своем двоичном механическом компьютере 1930-х годов Zuse Z1 . [3] Джеральд Б. Розенбергер из IBM подал заявку на патент на современный двоичный сумматор с переносом и прогнозированием в 1957 году. [4]
Двумя широко используемыми реализациями этой концепции являются сумматор Когге-Стоуна (KSA) и сумматор Брента-Кунга (BKA).
Теория работы
[ редактировать ]Добавление пульсации
[ редактировать ]Двоичный сумматор с пульсирующим переносом работает так же, как и большинство ручных методов сложения. Начиная с самой правой ( наименее значимой ) позиции, две соответствующие цифры складываются и получается результат. «Выполнение» может произойти, если для результата требуется более высокая цифра; например, «9 + 5 = 4, переноси 1». Двоичная арифметика работает таким же образом, но с меньшим количеством цифр. В этом случае возможны только четыре операции: 0+0, 0+1, 1+0 и 1+1; случай 1+1 генерирует перенос. Соответственно, все позиции цифр, кроме самой правой, должны ожидать возможности добавления дополнительной 1 из переноса цифр на одну позицию вправо.
Это означает, что ни одна цифровая позиция не может иметь абсолютно окончательного значения до тех пор, пока не будет установлено, идет ли перенос справа. Более того, если сумма без переноса является самым высоким значением в базе (9 в методе с карандашом и бумагой по основанию 10 или 1 в двоичной арифметике), невозможно сказать, будет ли данная позиция цифры передать перенос на позицию слева от него. В худшем случае, когда вся последовательность сумм достигает …99999999… (в десятичном формате) или …11111111… (в двоичном формате), вообще ничего невозможно вывести, пока не станет известно значение переноса, идущего справа; этот перенос должен распространяться влево, шаг за шагом, поскольку каждая позиция цифры оценивается как «9 + 1 = 0, перенос 1» или «1 + 1 = 0, перенос 1». Именно «рябь» переноса справа налево дала сумматору с пульсирующим переносом свое название и медлительность. Например, при сложении 32-битных целых чисел необходимо учитывать возможность того, что перенос может проходить через каждый из 32 однобитных сумматоров.
просмотр вперед
[ редактировать ]Перенос вперед зависит от двух вещей:
- Вычисление для каждой позиции цифры, будет ли эта позиция распространять перенос, если она входит справа.
- Объединение этих вычисленных значений позволяет быстро определить, будет ли для каждой группы цифр распространяться перенос, поступающий справа.
Предположим, что выбраны группы из четырех цифр. Последовательность событий будет такой:
- Все 1-битные сумматоры вычисляют свои результаты. Одновременно блоки прогнозирования выполняют свои расчеты.
- Предполагая, что перенос возникает в определенной группе, этот перенос появится в левом конце группы в течение максимум пяти задержек и начнет распространяться через группу слева от нее.
- Если этот перенос будет распространяться по всей следующей группе, модуль просмотра уже это вычислит. Соответственно, прежде чем перенос выйдет из следующей группы , блок прогнозирования немедленно (в пределах одной задержки) может сообщить следующей группе слева, что она собирается получить перенос, и в то же время сообщить следующая просматриваемая единица слева, о том, что перенос уже в пути.
Конечный эффект заключается в том, что переносы начинают с медленного распространения по каждой 4-битной группе, как в системе пульсирующего переноса, но затем движутся в четыре раза быстрее, перескакивая от одной единицы опережающего переноса к другой. Наконец, внутри каждой группы, которая получает перенос, перенос медленно распространяется внутри цифр в этой группе.
Чем больше битов в группе, тем сложнее становится логика опережающего переноса и тем больше времени тратится на «медленные пути» в каждой группе, а не на «быстрый путь» между группами (обеспечиваемый логикой опережающего переноса). . С другой стороны, чем меньше битов в группе, тем больше групп приходится пройти, чтобы добраться от одного конца числа до другого, и тем меньшее в результате ускорение получается.
Решение о размере группы, которое будет определяться логикой упреждающего переноса, требует детального анализа шлюзов и задержек распространения для конкретной используемой технологии.
Возможно иметь более одного уровня логики прогнозирования-переноса, и это обычно так и делается. Каждая единица опережающего переноса уже генерирует сигнал, говорящий: «Если перенос приходит справа, я буду распространять его влево», и эти сигналы можно объединить так, что каждая группа, скажем, из четырех единиц опережающего переноса становится частью «супергруппы», управляющей в общей сложности 16 битами добавляемых чисел. Логика опережающего переноса «супергруппы» сможет сказать, будет ли перенос, входящий в супергруппу, распространяться на всем ее пути, и, используя эту информацию, она сможет распространять переносы справа налево в 16 раз быстрее, чем наивный перенос. пульсирующий перенос. При такой двухуровневой реализации перенос может сначала распространяться по «медленному пути» отдельных сумматоров, а затем, достигнув левого конца своей группы, распространяться по «быстрому пути» 4-битного просмотра вперед. логику переноса, затем, достигнув левого конца своей супергруппы, распространяется по «сверхбыстрому пути» 16-битной логики прогнозного переноса.
Опять же, размеры групп, которые необходимо выбрать, зависят от точных деталей того, как быстро сигналы распространяются внутри логических элементов и от одного логического элемента к другому.
Для очень больших чисел (сотни или даже тысячи бит) логика опережающего переноса не становится более сложной, поскольку при необходимости можно добавить больше слоев супергрупп и суперсупергрупп. Увеличение количества вентилей также является умеренным: если все размеры групп равны четырем, в итоге получится одна треть от количества блоков прогнозного переноса, сколько имеется сумматоров. Однако «медленные дороги» на пути к более быстрым уровням начинают тормозить всю систему (например, 256-битный сумматор может иметь до 24 задержек вентиля при обработке переноса), и простая физическая передача Передача сигналов с одного конца длинного номера на другой становится проблемой. При таких размерах сумматоры с сохранением переноса предпочтительнее, поскольку они вообще не тратят время на распространение переноса.
Метод переноса вперед
[ редактировать ]Логика прогнозирования переноса использует концепции создания и распространения переносов. Хотя в контексте сумматора с переносом и прогнозированием наиболее естественно думать о генерации и распространении в контексте двоичного сложения, эти концепции можно использовать и в более общем смысле. В приведенных ниже описаниях цифра слова может быть заменена битом , когда речь идет о двоичном сложении 2.
сложение двух однозначных входных данных A и B Говорят, что генерируется , если сложение всегда будет иметь перенос, независимо от того, существует ли входной перенос (эквивалентно, независимо от того, переносятся ли какие-либо менее значащие цифры в сумме). Например, при десятичном сложении 52 + 67 сложение цифр десятков 5 и 6 генерируется , поскольку результат переносится на цифру сотен независимо от того, содержит ли цифра единиц; в примере единица не содержит цифр (2 + 7 = 9). Даже если бы числа были, скажем, 54 и 69, сложение цифр десятков 5 и 6 все равно дало бы результат , поскольку результат снова переходит в разряд сотен, несмотря на то, что 4 и 9 создают перенос.
В случае двоичного сложения генерирует тогда и только тогда, когда оба A и B равны 1. Если мы напишем представлять бинарный предикат, который истинен тогда и только тогда, когда генерирует, у нас есть
где является логическим союзом (т.е. и ).
сложение двух однозначных входных данных A и B Говорят, что распространяется, если сложение будет сохраняться всякий раз, когда есть входной перенос (эквивалентно, когда переносит следующая менее значащая цифра в сумме). Например, при десятичном сложении 37 + 62 сложение цифр десятков 3 и 6 распространяется , потому что результат перешел бы в разряд сотен, если бы единицы переносились (чего в этом примере этого не происходит). Обратите внимание, что распространение и генерация определяются относительно одной цифры сложения и не зависят ни от каких других цифр в сумме.
В случае двоичного сложения распространяется тогда и только тогда, когда хотя бы один из A или B равен 1. Если записывается для представления бинарного предиката, который истинен тогда и только тогда, когда распространяется, у человека есть
где в правой части уравнения находится логическая дизъюнкция (т. е. или ).
немного другое определение распространения Иногда используется . Согласно этому определению говорят, что A + B распространяется, если сложение будет переноситься всякий раз, когда есть входной перенос, но не будет переноситься, если входной перенос отсутствует. Из-за того, как генерация и распространение битов используются логикой переноса с опережением, не имеет значения, какое определение используется. В случае двоичного сложения это определение выражается формулой
где является исключающим или (т. е. исключающим ИЛИ ).
| Тип переноски | ||||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | Никто |
| 0 | 0 | 1 | 0 | Никто |
| 0 | 1 | 0 | 0 | Никто |
| 0 | 1 | 1 | 1 | Распространять |
| 1 | 0 | 0 | 0 | Никто |
| 1 | 0 | 1 | 1 | Распространять |
| 1 | 1 | 0 | 1 | Генерировать |
| 1 | 1 | 1 | 1 | Генерировать/Распространять |
Таблица, показывающая , когда переносы распространяются или генерируются.
Для двоичной арифметики или быстрее, чем xor , и для реализации требуется меньше транзисторов. Однако для многоуровневого сумматора с упреждением переноса проще использовать .
Учитывая эти концепции генерации и распространения, цифра сложения передается именно тогда, когда либо сложение генерируется , либо следующий менее значимый бит переносится и сложение распространяется. Написано на булевой алгебре, с бит переноса цифры i и и распространять и генерировать биты цифры i соответственно,
Детали реализации
[ редактировать ]

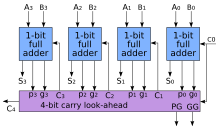
Для каждого добавляемого бита в двоичной последовательности логика прогнозирования переноса определяет, будет ли эта пара битов генерировать перенос или распространять перенос. Это позволяет схеме «предварительно обработать» два добавляемых числа, чтобы заранее определить перенос. Затем, когда выполняется фактическое сложение, не возникает задержки в ожидании эффекта пульсирующего переноса (или времени, необходимого для передачи переноса от первого полного сумматора к последнему полному сумматору).
Чтобы определить, будет ли битовая пара генерировать перенос, работает следующая логика:
Чтобы определить, будет ли битовая пара распространять перенос, можно использовать любое из следующих логических операторов:
Причина, по которой это работает, основана на оценке . Единственная разница в таблицах истинности между ( ) и ( ) это когда оба и равны 1. Однако если оба и равны 1, то член равен 1 (так как его уравнение ), и термин становится неактуальным. Исключающее ИЛИ обычно используется в базовой схеме полного сумматора; OR — это альтернативный вариант (только для упреждающего переноса), который намного проще с точки зрения количества транзисторов.
В приведенном примере логика генерации ( ) и распространять ( ) значения приведены ниже. Числовое значение определяет сигнал из приведенной выше схемы, начиная с 0 в крайнем правом углу до 3 в крайнем левом:
Замена в , затем в , затем в дает следующие расширенные уравнения:
4-битный сумматор с просмотром переноса также можно использовать в схеме более высокого уровня, если каждая логическая схема CLA генерирует сигнал для распространения и генерации в логическую схему CLA более высокого уровня. Группа распространяется ( ) и групповая генерация ( ) для 4-битного CLA:
Затем их можно использовать для создания переноса для этой конкретной 4-битной группы:
Видно, что это эквивалентно в предыдущих уравнениях.
Объединение четырех 4-битных CLA дает четыре групповых распространения и четыре групповых генерации. Блок упреждающего переноса (LCU) принимает эти 8 значений и использует идентичную логику для расчета. в CLA. Затем LCU генерирует вход переноса для каждого из 4 CLA и пятого, равного .
Вычисление задержки вентиля 16-битного сумматора (с использованием 4 CLA и 1 LCU) не так просто, как для сумматора со пульсирующим переносом.
Начиная с нулевого времени:
- расчет и выполняется в момент времени 1,
- расчет выполняется в момент времени 2,
- расчет выполняется в момент 3,
- Расчет входов для CLA от LCU выполняется по адресу:
- время 0 для первого CLA,
- время 5 для второго, третьего и четвертого CLA,
- расчет выполняются по адресу:
- время 4 для первого CLA,
- время 8 для второго, третьего и четвертого CLA,
- вычисление последнего бита переноса ( ) выполняется в момент 5.
Максимальное время составляет 8 задержек ворот (для ).
Стандартный 16-битный сумматор с пульсирующим переносом потребует 16 × 2 − 1 = 31 задержку вентиля.
Расширение
[ редактировать ]Этот пример представляет собой 4-битный сумматор с упреждающим переносом, имеет 5 выходов. Ниже представлено расширение:
S0 = (A0 XOR B0) XOR Cin '2dt (dt - delay time)
S1 = (A1 XOR B1)
XOR ((A0 AND B0)
OR ((A0 XOR B0) AND Cin)) '4dt
S2 = (A2 XOR B2)
XOR ((A1 AND B1)
OR ((A1 XOR B1) AND (A0 AND B0))
OR ((A1 XOR B1) AND (A0 XOR B0) AND Cin)) '4dt
S3 = (A3 XOR B3)
XOR ((A2 AND B2)
OR ((A2 XOR B2) AND (A1 AND B1))
OR ((A2 XOR B2) AND (A1 XOR B1) AND (A0 AND B0))
OR ((A2 XOR B2) AND (A1 XOR B1) AND (A0 XOR B0) AND Cin)) '4dt
Cout = (A3 AND B3)
OR ((A3 XOR B3) AND (A2 AND B2))
OR ((A3 XOR B3) AND (A2 XOR B2) AND (A1 AND B1))
OR ((A3 XOR B3) AND (A2 XOR B2) AND (A1 XOR B1) AND (A0 AND B0))
OR ((A3 XOR B3) AND (A2 XOR B2) AND (A1 XOR B1) AND (A0 XOR B0) AND Cin) '3dt
Более простой 4-битный сумматор с переносом и прогнозированием:
'Step 0
Gin = Cin '0dt
P00 = A0 XOR B0 '1dt
G00 = A0 AND B0 '1dt
P10 = A1 XOR B1 '1dt
G10 = A1 AND B1 '1dt
P20 = A2 XOR B2 '1dt
G20 = A2 AND B2 '1dt
P30 = A3 XOR B3 '1dt
G30 = A3 AND B3 '1dt
'Step 1
G01 = G00 OR_
P00 AND Gin '3dt, C0, valency-2
G11 = G10 OR_
P10 AND G00 OR_
P10 AND P00 AND Gin '3dt, C1, valency-3
G21 = G20 OR_
P20 AND G10 OR_
P20 AND P10 AND G00 OR_
P20 AND P10 AND P00 AND Gin '3dt, C2, valency-4
G31 = G30 OR_
P30 AND G20 OR_
P30 AND P20 AND G10 OR_
P30 AND P20 AND P10 AND G00 OR_
P30 AND P20 AND P10 AND P00 AND Gin '3dt, C3, valency-5
'Sum
S0 = P00 XOR Gin '2dt
S1 = P10 XOR G01 '4dt
S2 = P20 XOR G11 '4dt
S3 = P30 XOR G21 '4dt
S4 = G31 '3dt, Cout
Манчестерская цепь для переноски
[ редактировать ]Цепочка переноса Манчестера представляет собой разновидность сумматора с упреждающим переносом. [5] который использует общую логику для уменьшения количества транзисторов. Как видно выше в разделе реализации, логика генерации каждого переноса содержит всю логику, использованную для генерации предыдущих переносов. Цепочка переносов Манчестера генерирует промежуточные переносы, отводя узлы в вентиле, который вычисляет наиболее значимое значение переноса. Однако не все семейства логических устройств имеют эти внутренние узлы, CMOS основным примером которых является . Динамическая логика может поддерживать общую логику, как и шлюза передачи логика . Одним из основных недостатков манчестерской цепи переноса является то, что емкостная нагрузка всех этих выходов вместе с сопротивлением транзисторов приводит к тому, что задержка распространения увеличивается гораздо быстрее, чем при обычном упреждающем переносе. Длина секции манчестерской цепи переноса обычно не превышает 4 бит.
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ «Аналитическая машина - История аналитической машины Чарльза Бэббиджа» . история-компьютер.com . 4 января 2021 г. Проверено 19 июня 2021 г.
- ^ Бэббидж, Чарльз (1864). Отрывки из жизни философа . Лондон: Лонгман, Грин, Лонгманд Робертс и Грин. стр. 59–63 , 114–116.
- ^ Рохас, Рауль (07.06.2014). «Z1: Архитектура и алгоритмы первого компьютера Конрада Цузе». arXiv : 1406.1886 [ cs.AR ].
- ^ Розенбергер, Джеральд Б. (27 декабря 1960 г.). «Сумматор одновременного переноса» . Патент США 2966305.
- ^ «Манчестерский сумматор с цепочкой переноса — WikiChip» . ru.wikichip.org . Проверено 24 апреля 2017 г.
Дальнейшее чтение
[ редактировать ]- Аппаратные алгоритмы для арифметических модулей , исследовательская группа ARITH, лаборатория Аоки, Университет Тохоку.
- Кац, Рэнди (1994). Современный логический дизайн . Том. 26. Издательская компания Бенджамина/Каммингса . стр. 249–256 . дои : 10.1016/0026-2692(95)90052-7 . ISBN 0-8053-2703-7 .
{{cite book}}:|journal=игнорируется ( помогите ) - Савард, Джон Дж. Г. (2018) [2006]. «Продвинутые арифметические методы» . четырехблок . Архивировано из оригинала 3 июля 2018 г. Проверено 16 июля 2018 г.









































![{\displaystyle S_{[8-15]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c666dbc01c87fe0d2af0cd45e72b5d94cae780c9)