Напряжение цилиндра

В механике — напряжение в цилиндре это распределение напряжений с вращательной симметрией; то есть, который остается неизменным, если напряженный объект вращается вокруг некоторой фиксированной оси.

Модели напряжения в цилиндрах включают в себя:

• окружное напряжение , или кольцевое напряжение , нормальное напряжение в тангенциальном ( азимутальном ) направлении.
• осевое напряжение — нормальное напряжение, параллельное оси цилиндрической симметрии.
• радиальное напряжение — нормальное напряжение в направлениях, копланарных, но перпендикулярных оси симметрии.

Эти три главных напряжения — кольцевое, продольное и радиальное — можно рассчитать аналитически с использованием взаимно перпендикулярной трехосной системы напряжений.

Классическим примером (и тезкой) обручного напряжения является натяжение железных лент или обручей деревянной бочки . В прямой закрытой трубе любая сила, приложенная к стенке цилиндрической трубы из-за перепада давления , в конечном итоге приведет к возникновению кольцевых напряжений. Аналогично, если эта труба имеет плоские торцевые заглушки, любая сила, приложенная к ним статическим давлением, вызовет перпендикулярное осевое напряжение на той же стенке трубы. Тонкие сечения часто имеют пренебрежимо малое радиальное напряжение , но точные модели толстостенных цилиндрических оболочек требуют учета таких напряжений.

В толстостенных сосудах под давлением могут быть использованы методы строительства, позволяющие создать благоприятную структуру начальных напряжений. Эти сжимающие напряжения на внутренней поверхности уменьшают общее окружное напряжение в цилиндрах, находящихся под давлением. Цилиндрические сосуды такого типа обычно конструируются из концентрических цилиндров, сжатых друг в друга (или расширенных друг к другу), т. е. сборных термоусадочных цилиндров, но также могут быть изготовлены из отдельных цилиндров путем автофреттинга толстых цилиндров.

Определения

Стресс обруча

Компоненты окружного напряжения

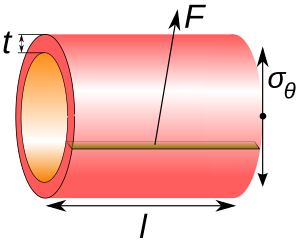
Окружное напряжение — это сила, действующая по окружности (перпендикулярно оси и радиусу объекта) в обоих направлениях на каждую частицу в стенке цилиндра. Его можно описать как:

$\sigma _{\theta }={\dfrac {F}{tl}}\$

где:

• F — сила , действующая по окружности на участок стенки цилиндра, сторона которого имеет следующие две длины:
• t - радиальная толщина цилиндра
• l — осевая длина цилиндра.

Альтернативой окружному напряжению при описании окружного напряжения является напряжение стенки или натяжение стенки ( T ), которое обычно определяется как общая окружная сила, действующая по всей радиальной толщине:

$T={\dfrac {F}{l}}\$

Цилиндрические координаты

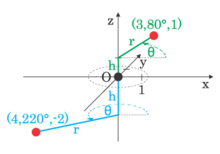
Наряду с осевым напряжением и радиальным напряжением окружное напряжение является компонентой тензора напряжений в цилиндрических координатах .

Обычно полезно разложить любую силу, приложенную к объекту с вращательной симметрией , на компоненты, параллельные цилиндрическим координатам r , z и θ . Эти компоненты силы вызывают соответствующие напряжения: радиальное напряжение, осевое напряжение и кольцевое напряжение соответственно.

Связь с внутренним давлением

Тонкостенное предположение

Чтобы предположение о тонкостенности было действительным, толщина стенки сосуда должна составлять не более одной десятой (часто называемой диаметром / t> 20) его радиуса. Это позволяет рассматривать стенку как поверхность и впоследствии использовать уравнение Юнга – Лапласа для оценки окружного напряжения, создаваемого внутренним давлением на тонкостенном цилиндрическом сосуде под давлением:

$\sigma _{\theta }={\dfrac {Pr}{t}}\$ (для цилиндра)

$\sigma _{\theta }={\dfrac {Pr}{2t}}\$ (для сферы)

где

• P — внутреннее давление
• t - толщина стенки
• r - средний радиус цилиндра
• $\sigma _{\theta }\!$ это напряжение обруча.

Уравнение кольцевого напряжения для тонких оболочек приближенно справедливо и для сферических сосудов, в том числе для растительных клеток и бактерий, в которых внутреннее тургорное давление может достигать нескольких атмосфер. В практических инженерных приложениях для цилиндров (труб и трубок) окружное напряжение часто преобразуется в давление и называется формулой Барлоу .

в системе дюйм-фунт-секунда (IPS) Единицы измерения P — это фунт-сила на квадратный дюйм (psi). Единицами t и d являются дюймы (дюймы).Единицами СИ для P являются паскали (Па), а t и d =2 r — метры (м).

Когда сосуд имеет закрытые концы, на них действует внутреннее давление, развивающее силу вдоль оси цилиндра. Оно известно как осевое напряжение и обычно меньше окружного напряжения.

$\sigma _{z}={\dfrac {F}{A}}={\dfrac {Pd^{2}}{(d+2t)^{2}-d^{2}}}\$

Хотя это можно приблизить к

$\sigma _{z}={\dfrac {Pr}{2t}}\$

Также существует радиальное напряжение. $\sigma _{r}\$ которая развита перпендикулярно поверхности и может быть оценена в тонкостенных цилиндрах как:

$\sigma _{r}={-P}\$

В предположении тонкостенности соотношение ${\dfrac {r}{t}}\$ велика, поэтому в большинстве случаев эту составляющую считают незначительной по сравнению с окружным и осевым напряжениями.

Толстостенные сосуды

Если исследуемый цилиндр имеет ${\text{radius}}/{\text{thickness}}$ соотношение менее 10 (часто упоминается как ${\text{diameter}}/{\text{thickness}}<20$) уравнения тонкостенного цилиндра больше не выполняются, поскольку напряжения на внутренней и внешней поверхностях значительно различаются, и напряжением сдвига в поперечном сечении больше нельзя пренебрегать.

Эти напряжения и деформации можно рассчитать с помощью уравнений Ламе : система уравнений, разработанная французским математиком Габриэлем Ламе .

$\sigma _{r}=A-{\dfrac {B}{r^{2}}}\$

$\sigma _{\theta }=A+{\dfrac {B}{r^{2}}}\$

где:

$A$ и $B$ – константы интегрирования, которые можно найти из граничных условий,

$r$ — радиус интересующей точки (например, внутренней или внешней стены).

Для цилиндра с граничными условиями:

$p(r=a)=P_{a}$ (т.е. внутреннее давление $P_{a}$ на внутренней поверхности),

$p(r=b)=P_{b}$ (т.е. внешнее давление $P_{b}$ на внешней поверхности),

получаются следующие константы:

$A={\dfrac {P_{a}a^{2}-P_{b}b^{2}}{b^{2}-a^{2}}}\$,

$B={\dfrac {a^{2}b^{2}(P_{a}-P_{b})}{b^{2}-a^{2}}}\$.

Используя эти константы, получаем следующее уравнение для окружного напряжения:

$\sigma _{\theta }={\dfrac {P_{a}a^{2}-P_{b}b^{2}}{b^{2}-a^{2}}}+{\dfrac {a^{2}b^{2}(P_{a}-P_{b})}{(b^{2}-a^{2})r^{2}}}\$

Для сплошного цилиндра: $R_{i}=0$ затем $B=0$ а твердый цилиндр не может иметь внутреннего давления, поэтому $A=P_{o}$.

Так как для толстостенных цилиндров соотношение ${\dfrac {r}{t}}\$ меньше 10, радиальное напряжение, пропорционально другим напряжениям, становится значительным (т. е. P больше не намного, намного меньше, чем Pr/t и Pr/2t), и поэтому толщина стенки становится основной внимание к дизайну (Харви, 1974, стр. 57).

В теории сосудов под давлением любой элемент стенки оценивается в трехосной системе напряжений, причем тремя главными напряжениями являются окружное, продольное и радиальное. Следовательно, по определению не существует касательных напряжений в поперечной, тангенциальной или радиальной плоскостях.

В толстостенных цилиндрах максимальное касательное напряжение в любой точке определяется половиной алгебраической разности между максимальным и минимальным напряжениями, которая, следовательно, равна половине разности между кольцевым и радиальным напряжениями. Напряжение сдвига достигает максимума на внутренней поверхности, что важно, поскольку оно служит критерием разрушения, поскольку оно хорошо коррелирует с реальными испытаниями на разрыв толстых цилиндров (Harvey, 1974, стр. 57).

Практические эффекты

Инженерное дело

Разрушение определяется окружным напряжением в отсутствие других внешних нагрузок, поскольку оно является самым большим главным напряжением. Обратите внимание, что наибольшее напряжение обруч испытывает внутри (снаружи и внутри наблюдается одинаковая общая нагрузка, которая распределяется по разным окружностям); следовательно, трещины в трубах теоретически должны начинаться изнутри трубы. Вот почему проверки труб после землетрясений обычно включают в себя помещение камеры внутрь трубы для проверки на наличие трещин.Податливость определяется эквивалентным напряжением, которое включает окружное напряжение и продольное или радиальное напряжение, если оно отсутствует.

Лекарство

При патологии или стенок сосудов желудочно -кишечного тракта напряжение стенки представляет собой мышечное напряжение стенки сосуда. В результате закона Лапласа , если в стенке кровеносного сосуда образуется аневризма , радиус сосуда увеличивается. Это означает, что внутренняя сила, действующая на сосуд, уменьшается, и, следовательно, аневризма будет продолжать расширяться, пока не разорвется. Похожая логика применима и к образованию дивертикулов в кишечнике .

Разработка теории

Чугунная опора железнодорожного моста Чепстоу , 1852 год. Обручи из кованого железа с шарнирными соединениями (более прочные на растяжение, чем чугун) сопротивляются окружным напряжениям.

Первый теоретический анализ напряжения в цилиндрах был разработан инженером середины 19-го века Уильямом Фэйрберном при содействии его математического аналитика Итона Ходжкинсона . Их первый интерес заключался в изучении конструкции и неисправностей паровых котлов . Фэйрберн понял, что окружное напряжение в два раза превышает продольное напряжение, что является важным фактором при сборке корпусов котлов из катаных листов, соединенных клепкой . Позже работы были применены к строительству мостов и изобретению коробчатой ​​балки . В Чепстоуском железнодорожном мосту чугунные опоры укреплены внешними полосами из кованого железа . Вертикальная, продольная сила – это сжимающая сила, которой чугун хорошо способен противостоять. Окружное напряжение является растягивающим, поэтому добавляется кованое железо, материал с большей прочностью на разрыв, чем чугун.

См. также

• Может быть вызвано перегрузкой цилиндра:
  • Бостонская патоковая катастрофа
  • Взрыв котла
  • Кипящая жидкость, расширяющаяся, взрыв пара
• Сопутствующие инженерные темы:
  • Концентрация стресса
  • Гидростатические испытания
  • коробление
  • Артериальное давление#Relation_to_wall_tension
  • Трубопровод#Stress_anaанализ
• Проекты, на которые сильно влияет этот стресс:
  • Сосуд под давлением
    • Ракетный двигатель
  • Маховик
  • Купол Флорентийского собора

Ссылки

• Тонкостенные сосуды под давлением . 19 июня 2008 г. {{cite book}}: |work= игнорируется ( помогите )