Псевдолес

1-лес (максимальный псевдолес), образованный тремя 1-деревьями.

В теории графов псевдолес — это неориентированный граф. в котором каждая компонента связности имеет не более одного цикла . То есть это система вершин и ребер , соединяющая пары вершин, такая, что никакие два цикла последовательных ребер не имеют общей вершины друг с другом, и никакие два цикла не могут быть соединены друг с другом путем последовательных ребер. Псевдодерево — это связный псевдолес.

Названия обоснованы аналогией с наиболее часто изучаемыми деревьями и лесами . (Дерево — это связный граф без циклов; лес — это непересекающееся объединение деревьев.) Габоу и Тарьян приписывают изучение псевдолесов книге Данцига 1963 года по линейному программированию , в которой псевдолеса возникают при решении определенных задач сетевых потоков . Псевдолеса также образуют модели функций на основе теории графов и встречаются в ряде алгоритмических задач. Псевдолеса представляют собой разреженные графы : число ребер в них линейно ограничено числом вершин (на самом деле у них не более столько ребер, сколько вершин) — а их матроидная структура позволяет разложить несколько других семейств разреженных графов. как союзы лесов и псевдолесов. Название «псевдолес» взято из работы Picard & Queyranne (1982) .

Определения и структура

Мы определяем неориентированный граф как набор вершин и ребер , в котором каждое ребро имеет две вершины (которые могут совпадать) в качестве конечных точек. То есть мы допускаем наличие нескольких ребер (ребер с одной и той же парой конечных точек) и петель (ребер, две конечные точки которых являются одной и той же вершиной). Подграф . графа — это граф, образованный любыми подмножествами его вершин и ребер, такими, что каждое ребро в подмножестве ребер имеет обе конечные точки в подмножестве вершин Компонент связности неориентированного графа — это подграф, состоящий из вершин и ребер, до которых можно добраться, пройдя по ребрам из одной заданной начальной вершины. Граф связный, если каждая вершина или ребро достижимы из любой другой вершины или ребра. Цикл в неориентированном графе — это связный подграф , в котором каждая вершина инцидентна ровно двум ребрам, или является петлей.

21 унициклический граф с не более чем шестью вершинами.

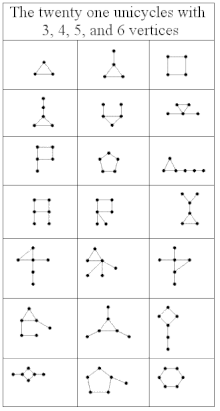
Псевдолес — это неориентированный граф, в котором каждая компонента связности содержит не более одного цикла. Эквивалентно, это неориентированный граф, в котором каждый компонент связности имеет не больше ребер, чем вершин. Компоненты, не имеющие циклов, являются просто деревьями , а компоненты, содержащие один цикл, называются 1-деревьями или унициклическими графами . То есть 1-дерево — это связный граф, содержащий ровно один цикл. Псевдолес с одним связным компонентом (обычно называемый псевдодеревом , хотя некоторые авторы определяют псевдодерево как 1-дерево) является либо деревом, либо 1-деревом; Как правило, псевдолес может иметь несколько связных компонентов, если все они являются деревьями или 1-деревьями.

Если удалить из 1-дерева одно из ребер в его цикле, результатом будет дерево. Обращая этот процесс, если кто-то дополняет дерево, соединяя любые две его вершины новым ребром, результатом будет 1-дерево; путь в дереве, соединяющий две конечные точки добавленного ребра, вместе с самим добавленным ребром образуют уникальный цикл 1-дерева. Если кто-то дополняет 1-дерево, добавляя ребро, которое соединяет одну из его вершин с вновь добавленной вершиной, результатом снова будет 1-дерево с еще одной вершиной; альтернативный метод построения 1-деревьев — начать с одного цикла, а затем повторить эту операцию увеличения любое количество раз. Ребра любого 1-дерева можно единственным образом разбить на два подграфа, один из которых является циклом, а другой - лесом, так что каждое дерево леса содержит ровно одну вершину цикла.

Изучены также некоторые более конкретные типы псевдолесов.

, 1-лес иногда называемый максимальным псевдолесом , — это псевдолес, в который нельзя добавить больше ребер без того, чтобы какой-либо компонент графа не содержал несколько циклов. Если псевдолес содержит дерево в качестве одного из своих компонентов, он не может быть 1-лесом, поскольку можно добавить либо ребро, соединяющее две вершины внутри этого дерева, образуя один цикл, либо ребро, соединяющее это дерево с каким-либо другим компонентом. Таким образом, 1-леса — это в точности псевдолеса, в которых каждый компонент является 1-деревом.

Охватывающие псевдолеса неориентированного графа G псевдолеса это подграфы G , которые имеют все вершины G. — Такой псевдолес не обязательно должен иметь ребра, поскольку, например, подграф, который имеет все вершины G и не имеет ребер, является псевдолесом (компонентами которого являются деревья, состоящие из одной вершины).

Максимальные псевдолеса G — это подграфы псевдолесов G , которые не содержатся ни в каком более крупном G. псевдолесе Максимальный псевдолес G всегда является остовным псевдолесом, но не наоборот. Если G не имеет связных компонентов, которые являются деревьями, то его максимальные псевдолеса являются 1-лесами, но если G имеет древесный компонент, его максимальные псевдолеса не являются 1-лесами. Точнее говоря, в любом графе G его максимальные псевдолеса состоят из каждого компонента дерева G вместе с одним или несколькими непересекающимися 1-деревьями, покрывающими остальные вершины G .

Направленные псевдолеса

Версии этих определений также используются для ориентированных графов . Как и неориентированный граф, ориентированный граф состоит из вершин и ребер, но каждое ребро направлено от одной из его конечных точек к другой конечной точке. — Ориентированный псевдолес это ориентированный граф, в котором каждая вершина имеет не более одного исходящего ребра; то есть имеет выходную степень не более одной. Направленный 1-лес , чаще всего называемый функциональным графом (см. ниже ), иногда максимальным направленным псевдолесом , представляет собой ориентированный граф, в котором каждая вершина имеет исходящую степень ровно одну. Если D — ориентированный псевдолес, неориентированный граф, образованный удалением направления из каждого ребра D, является неориентированным псевдолесом.

Количество ребер

Каждый псевдолес на множестве из n вершин имеет не более n ребер, а каждый максимальный псевдолес на множестве из n вершин имеет ровно n ребер. И наоборот, если граф G обладает свойством, что для каждого подмножества S его вершин количество ребер в индуцированном подграфе S является не превышает количества вершин в S , то G псевдолесом. 1-деревья можно определить как связные графы с одинаковым количеством вершин и ребер.

Переходя от отдельных графов к семействам графов, если семейство графов обладает свойством, что каждый подграф графа в семействе также входит в семейство, и каждый граф в семействе имеет не более чем столько же ребер, сколько и вершин, то семейство содержит только псевдолеса. Например, каждый подграф трекла ( граф, нарисованный так, что каждая пара ребер имеет одну точку пересечения) также является треклом, поэтому гипотезу Конвея о том, что каждый трекл имеет не более чем столько же ребер, сколько и вершин, можно переформулировать следующим образом: Тракл — это псевдолес. Более точная характеристика состоит в том, что если гипотеза верна, то треклы - это в точности псевдолеса без четырехвершинного цикла и не более чем с одним нечетным циклом.

Стрейну и Теран обобщают условия разреженности, определяющие псевдолеса: они определяют граф как ( k , l )-разреженный, если каждый непустой подграф с n вершинами имеет не более kn − l ребер, и ( k , l )-плотный, если он ( k , l ) -плотный )-разреженным и имеет ровно kn − l ребер. Таким образом, псевдолеса представляют собой (1,0)-разреженные графы, а максимальные псевдолеса — это (1,0)-плотные графы. Несколько других важных семейств графов могут быть определены из других значений k и l :а когда l ≤ k, ( k , l )-разреженные графы можно охарактеризовать как графы, образованные как непересекающееся по ребрам объединение l лесов и k − l псевдолесов.

Почти каждый достаточно разреженный случайный граф является псевдолесом. То есть, если c — константа с 0 < c < 1/2, а P _c ( n ) — вероятность того, что равномерный случайный выбор среди графов с n -вершинами с cn ребрами приведет к образованию псевдолеса, то P _c ( n ) стремится к единице в пределе при больших n . Однако при c > 1/2 почти каждый случайный граф с cn ребер имеет большую компоненту, не являющуюся одноциклической.

Перечисление

Граф является простым , если в нем нет петель и кратных ребер с одинаковыми концами. Количество простых 1-деревьев с n помеченными вершинами равно

$n\sum _{k=1}^{n}{\frac {(-1)^{k-1}}{k}}\sum _{n_{1}+\cdots +n_{k}=n}{\frac {n!}{n_{1}!\cdots n_{k}!}}{\binom {{\binom {n_{1}}{2}}+\cdots +{\binom {n_{k}}{2}}}{n}}.$

Значения для n до 300 можно найти в последовательности OEIS : A057500 Электронной энциклопедии целочисленных последовательностей .

Число максимальных направленных псевдолесов на n вершинах, допускающих самоциклы, равно n ^н , поскольку для каждой вершины существует n возможных концов исходящего ребра. Андре Жуайал использовал этот факт, чтобы обеспечить взаимно однозначное доказательство формулы Кэли о том, что количество неориентированных деревьев на n узлах равно n. ^{п - 2} , находя биекцию между максимальными направленными псевдолесами и неориентированными деревьями с двумя выделенными узлами. Если самоциклы не разрешены, вместо этого количество максимальных направленных псевдолесов равно ( n - 1) ^н .

Графики функций

«Функциональный график» перенаправляется сюда. Чтобы узнать о других значениях, см. График функции .

Функция из множества {0,1,2,3,4,5,6,7,8} до себя и соответствующий функциональный график

Направленные псевдолеса и эндофункции в некотором смысле математически эквивалентны. Любую функцию ƒ из множества X в себя (то есть эндоморфизм X ) всякий можно интерпретировать как определение направленного псевдолеса, который имеет ребро от x до y раз, когда ƒ( x ) = y . Результирующий направленный псевдолес является максимальным и может включать в себя циклы всякий раз, когда некоторое значение x имеет ƒ( x ) = x . В качестве альтернативы, исключение самоциклов приводит к немаксимальному псевдолесу. В другом направлении любой максимальный направленный псевдолес определяет функцию ƒ такую, что ƒ( x ) является целью ребра, исходящего из x , а любой немаксимальный направленный псевдолес можно сделать максимальным, добавив циклы и затем преобразуя в функцию таким же образом. По этой причине максимальные направленные псевдолеса иногда называют функциональными графами . Просмотр функции как функционального графа обеспечивает удобный язык для описания свойств, которые не так легко описать с точки зрения теории функций; этот метод особенно применим к задачам, связанным с повторяющимися функциями , которые соответствуют путям в функциональных графах.

Обнаружение цикла , проблема следования по пути в функциональном графе, чтобы найти в нем цикл, имеет приложения в криптографии и вычислительной теории чисел , как часть ро-алгоритма Полларда для факторизации целых чисел и как метод поиска коллизий в криптографических хэш-функциях . Ожидается, что в этих приложениях ƒ будет вести себя случайным образом; Флажоле и Одлизко изучить теоретико-графовые свойства функциональных графов, возникающих в результате случайно выбранных отображений. В частности, форма парадокса дня рождения подразумевает, что в случайном функциональном графе с n вершинами путь, начинающийся со случайно выбранной вершины, обычно зацикливается на самом себе, образуя цикл за O( √ n ) шагов. Конягин и др. добились аналитического и вычислительного прогресса в графовой статистике.

Мартин, Одлизко и Вольфрам исследовать псевдолеса, моделирующие динамику клеточных автоматов . Эти функциональные графы, которые они называют диаграммами переходов состояний , имеют по одной вершине для каждой возможной конфигурации, в которой может находиться ансамбль ячеек автомата, и ребро, соединяющее каждую конфигурацию с следующей за ней конфигурацией по правилу автомата. Из структуры этих диаграмм можно вывести свойства автомата, такие как количество компонентов, длина предельных циклов, глубина деревьев, соединяющих непредельные состояния с этими циклами, или симметрия диаграммы. Например, любая вершина без входящего края соответствует узору «Райский сад» , а вершина с замкнутым контуром соответствует узору натюрморта .

Еще одним ранним применением функциональных графов являются поезда , используемые для изучения систем троек Штейнера . Последовательность тройной системы представляет собой функциональный граф, имеющий вершину для каждой возможной тройки символов; каждая тройка pqr отображается с помощью ƒ в stu , где pqs , prt и qru — тройки, принадлежащие системе троек и содержащие пары pq , pr и qr соответственно. Было показано, что поезда являются мощным инвариантом тройных систем, хотя и несколько громоздки для вычислений.

Бициркулярный матроид

Матроид — это математическая структура , в которой определенные наборы элементов определены как независимые таким образом, что независимые наборы удовлетворяют свойствам, смоделированным после свойств линейной независимости в векторном пространстве . Одним из стандартных примеров матроида является графический матроид , в котором независимыми множествами являются множества ребер в лесах графа; матроидная структура лесов важна в алгоритмах вычисления минимального остовного дерева графа. Аналогично мы можем определить матроидов из псевдолесов.

Для любого графа G = ( V , E ) мы можем определить матроид на ребрах G , в котором набор ребер независим тогда и только тогда, когда он образует псевдолес; этот матроид известен как бициркулярный матроид (или велосипедный матроид ) G . Наименьшими зависимыми множествами для этого матроида являются минимальные связные подграфы G , имеющие более одного цикла, и эти подграфы иногда называют велосипедами. Существует три возможных типа велосипеда: тета-граф имеет две вершины, которые соединены тремя внутренне непересекающимися путями, граф в форме восьмерки состоит из двух циклов, разделяющих одну вершину, и граф наручников состоит из двух непересекающихся циклов, соединенных путем. . Граф является псевдолесом тогда и только тогда, когда он не содержит велосипеда в качестве подграфа.

Запрещенные несовершеннолетние

Граф -бабочка (слева) и ромбовидный граф (справа), запрещенные миноры для псевдолесов.

Формирование второстепенного псевдолеса путем сжатия некоторых его краев и удаления других приводит к созданию другого псевдолеса. Следовательно, семейство псевдолесов замкнуто относительно миноров, а из теоремы Робертсона-Сеймура следует, что псевдолеса можно охарактеризовать в терминах конечного набора запрещенных миноров , аналогично теореме Вагнера, характеризующей плоские графы как графы, не имеющие ни полного графа K _5, ни полный двудольный граф K _3,3 как миноры.Как обсуждалось выше, любой граф, не являющийся псевдолесом, содержит в качестве подграфа наручник, цифру 8 или тэта-граф; любой граф наручников или фигура 8 может быть сжат до образования графа-бабочки (пятивершинная фигура 8), а любой тэта-граф может быть сжат до образования ромбовидного графа (тета-граф с четырьмя вершинами), поэтому любой непсевдолес содержит либо бабочку, либо ромб в качестве минора, и это единственные минорно-минимальные графы, не являющиеся псевдолесами. Таким образом, граф является псевдолесом тогда и только тогда, когда в нем нет ни бабочки, ни ромба в качестве минора. Если запретить только ромб, но не бабочку, в результате получится более крупное семейство графов, состоящее из графов-кактусов и непересекающихся объединений нескольких графов-кактусов.

Проще говоря, если рассматривать мультиграфы с петельками , то существует только один запрещенный минор — вершина с двумя петлями.

Алгоритмы

Раннее алгоритмическое использование псевдолесов включает сетевой симплексный алгоритм и его применение к задачам обобщенного потока, моделирующим преобразование между товарами разных типов. В этих задачах в качестве входных данных предоставляется потоковая сеть , в которой вершины моделируют каждый товар, а ребра моделируют допустимые преобразования между одним товаром и другим. Каждое ребро отмечено мощностью ( какая часть товара может быть преобразована в единицу времени), множителем потока (коэффициент конверсии между товарами) и стоимостью (сколько потерь или, если оно отрицательное, прибыли понесено на единицу продукции). конверсия). Задача состоит в том, чтобы определить, какое количество каждого товара необходимо конвертировать через каждое ребро сети потоков, чтобы минимизировать затраты или максимизировать прибыль, соблюдая при этом ограничения мощности и не позволяя товарам любого типа накапливаться неиспользованными. Задачу такого типа можно сформулировать в виде линейной программы и решить с помощью симплексного алгоритма . Промежуточные решения, возникающие в результате этого алгоритма, а также окончательное оптимальное решение имеют особую структуру: каждое ребро во входной сети либо не используется, либо используется на полную мощность, за исключением подмножества ребер, образующих охватывающий псевдолес из входную сеть, для которой объемы потоков могут находиться в диапазоне от нуля до полной мощности. В этом приложении унициклические графы также иногда называются Дополненные деревья и максимальные псевдолеса также иногда называют дополненными лесами .

Задача о минимальном остовном псевдолесе включает в себя поиск остовного псевдолеса минимального веса в большем взвешенном по ребрам графе G .Из-за матроидной структуры псевдолесов максимальные псевдолеса с минимальным весом могут быть найдены с помощью жадных алгоритмов, аналогичных алгоритмам для задачи минимального остовного дерева . Однако в этом случае Габоу и Тарьян нашли более эффективный подход с использованием линейного времени.

Псевдодревесность определяется графа G по аналогии с древесностью как минимальное число псевдолесов, на которые можно разбить его ребра; эквивалентно, это минимум k такой, что G является ( k ,0)-разреженным, или минимальный k такой, что ребра G могут быть ориентированы так, чтобы сформировать ориентированный граф с исходящей степенью не более k . Благодаря матроидной структуре псевдолесов псевдодревесность может быть вычислена за полиномиальное время.

Случайный ребер , двудольный граф с n вершинами на каждой стороне его двудольного деления и cn выбранных независимо случайным образом из каждого из n ² возможных пар вершин с высокой вероятностью является псевдолесом, если c константа строго меньше единицы. Этот факт играет ключевую роль в анализе хеширования с кукушкой — структуры данных для поиска пар ключ-значение путем просмотра в одной из двух хеш-таблиц мест, определенных по ключу: можно сформировать граф, «граф с кукушкой», вершины которого соответствуют местоположениям хэш-таблицы, а ребра соединяют два местоположения, в которых может быть найден один из ключей, а алгоритм хеширования кукушки успешно находит местоположения для всех своих ключей тогда и только тогда, когда граф кукушки является псевдолесом.

Псевдолеса также играют ключевую роль в параллельных алгоритмах раскраски графов и связанных с ними задачах.

Ссылки

• Ахуджа, Равиндра К .; Маньянти, Томас Л .; Орлин, Джеймс Б. (1993), Сетевые потоки: теория, алгоритмы и приложения , Прентис Холл, ISBN  0-13-617549-Х .
• Айгнер, Мартин ; Циглер, Гюнтер М. (1998), Доказательства из КНИГИ , Springer-Verlag , стр. 141–146 .
• Альварес, Карме; Блеса, Мария; Серна, Мария (2002), «Универсальная устойчивость неориентированных графов в состязательной модели массового обслуживания», Proc. 14-й симпозиум ACM по параллельным алгоритмам и архитектурам , стр. 183–197, doi : 10.1145/564870.564903 , hdl : 2117/97553 , S2CID   14384161 .
• Боллобас, Бела (1985), Случайные графики , Academic Press .
• Колборн, Марлен Дж.; Колборн, Чарльз Дж .; Розенбаум, Уилф Л. (1982), «Поезда: инвариант для тройных систем Штейнера», Ars Combinatoria , 13 : 149–162, MR   0666934 .
• Данциг, Великобритания (1963), Линейное программирование и расширения , Princeton University Press .
• Эль-Маллах, Эхаб; Колборн, Чарльз Дж. (1988), «Сложность некоторых проблем с удалением ребер», IEEE Transactions on Circuits and Systems , 35 (3): 354–362, doi : 10.1109/31.1748 .
• Флажоле, П. ; Одлизко, А. (1990), «Статистика случайных отображений», Достижения в криптологии - EUROCRYPT '89: Семинар по теории и применению криптографических методов , Конспекты лекций по информатике, том. 434, Springer-Verlag, стр. 329–354 .
• Габоу, Гонконг ; Тарьян, Р.Э. (1988), «Алгоритм линейного времени для поиска минимального охвата псевдолеса», Information Processing Letters , 27 (5): 259–263, doi : 10.1016/0020-0190(88)90089-0 .
• Габоу, Гонконг ; Вестерманн, Х.Х. (1992), «Леса, фреймы и игры: алгоритмы матроидных сумм и приложений», Algorithmica , 7 (1): 465–497, doi : 10.1007/BF01758774 , S2CID   40358357 .
• Гольдберг, А.В. ; Плоткин, С.А.; Шеннон, GE (1988), «Параллельное нарушение симметрии в разреженных графах» , SIAM Journal on Discrete Mathematics , 1 (4): 434–446, doi : 10.1137/0401044 .
• Конягин, Сергей; Лука, Флориан; Манс, Бернар; Мэтисон, Люк; Шпарлинский, Игорь Е. (2010), Функциональные графы полиномов над конечными полями
• Ковалик, Л. (2006), «Схема аппроксимации для наименьшей исходящей степени ориентации и мер плотности графа», в Асано, Тецуо (редактор), Труды Международного симпозиума по алгоритмам и вычислениям , Конспекты лекций по информатике, том. 4288, Springer-Verlag, стр. 557–566, номер doi : 10.1007/11940128 , ISBN.  978-3-540-49694-6 .
• Краскал, Клайд П .; Рудольф, Ларри; Снир, Марк (1990), «Эффективные параллельные алгоритмы для задач на графах», Algorithmica , 5 (1): 43–64, doi : 10.1007/BF01840376 , S2CID   753980 .
• Пикард, Жан-Клод; Кейранн, Морис (1982), «Решение сетевых потоков некоторых задач нелинейного программирования 0–1 с приложениями к теории графов», Networks , 12 (2): 141–159, doi : 10.1002/net.3230120206 , MR   0670021 .
• Куцельнигг, Рейнхард (2006), «Двудольные случайные графы и хеширование с кукушкой» , Четвертый коллоквиум по математике и информатике , Дискретная математика и теоретическая информатика, том. АГ, стр. 403–406 .
• Ловас, Л. ; Пах, Дж.; Сегеди, М. (1997), «О гипотезе Конвея о трекле», Дискретная и вычислительная геометрия , 18 (4): 369–376, doi : 10.1007/PL00009322 .
• Мартин, О.; Одлизко, А.М. ; Вольфрам, С. (1984), «Алгебраические свойства клеточных автоматов» , Communications in Mathematical Physics , 93 (2): 219–258, Bibcode : 1984CMaPh..93..219M , CiteSeerX   10.1.1.78.212 , doi : 10.1007 /BF01223745 , S2CID   6900060 , заархивировано из оригинала 12 февраля 2012 г. , получено 03 октября 2007 г.
• Мэтьюз, Л.Р. (1977), «Бициркульные матроиды», Ежеквартальный журнал математики , вторая серия, 28 (110): 213–227, doi : 10.1093/qmath/28.2.213 , MR   0505702 .
• Ридделл, Р.Дж. (1951), Вклад в теорию конденсации , доктор философии. диссертация, Анн-Арбор: Мичиганский университет, бибкод : 1951PhDT.......20R .
• Симоэс-Перейра, Дж. М. С. (1972), «О подграфах как матроидных клетках», Mathematical Journal , 127 (4): 315–322, doi : 10.1007/BF01111390 , S2CID   186231673 .
• Стинсон, Д.Р. (1983), «Сравнение двух инвариантов тройных систем Штейнера: фрагменты и поезда», Ars Combinatoria , 16 : 69–76, MR   0734047 .
• Стрейну, И. ; Теран, Л. (2009), «Разложение графов, подтверждающее разреженность», Graphs and Combinatorics , 25 (2): 219, arXiv : 0704.0002 , doi : 10.1007/s00373-008-0834-4 , S2CID   15877017 .
• Уайт, HS (1913), «Тройные системы как преобразования и их пути среди триад», Transactions of the American Mathematical Society , 14 (1), American Mathematical Society: 6–13, doi : 10.2307/1988765 , JSTOR   1988765 .
• Уайтли, В. (1988), «Объединение матроидов и жесткость каркасов», SIAM Journal on Discrete Mathematics , 1 (2): 237–255, doi : 10.1137/0401025 .
• Вудалл, Д.Р. (1969), «Траклс и тупик», на валлийском языке, DJA (редактор), «Комбинаторная математика и ее приложения» , Academic Press, стр. 335–348 .

Внешние ссылки

• Вайсштейн, Эрик В. , «Унициклический граф» , MathWorld