Анализ дерева предметов

Анализ дерева элементов ( ITA ) — это метод анализа данных , который позволяет построитьиерархическая структура пунктов анкеты или теста на основе наблюдаемого ответаузоры.
Предположим, что у нас есть анкета с m пунктами и испытуемые могутответьте положительно (1) или отрицательно (0) на каждый из этих пунктов, т.е. дихотомический . Если n испытуемых отвечают на вопросы, в результате получается двоичных данных матрица D. с m столбцами и n строками.Типичными примерами этого формата данных являются тестовые задания, которые можно решить (1) или не выполнить.(0) по субъектам. Другими типичными примерами являются анкеты, в которых пунктыутверждения, с которыми испытуемые могут согласиться (1) или не согласиться (0).
В зависимости от содержания пунктов возможно, что ответ субъекта напункт j определяет ее или его ответы на другие вопросы. Например, возможно, чтокаждый субъект, который согласен с пунктом j, также согласится и с пунктом i . В этом случае мы говорим, чтопункт j подразумевает пункт i (сокращенно $i\rightarrow j$ ). Цель ITA – выявить такие детерминированные последствия из набора данных D .

Алгоритмы для ITA

ITA был первоначально разработан Ван Леуве в 1974 году. ^[1] Результат его алгоритма ,который мы в дальнейшем будем называть классическим ITA , представляет собой логически непротиворечивый наборподразумеваемое $i\rightarrow j$ . Логическая последовательность означает, что если из i следует j, а из j следует k, то из i следует k для каждой тройки i , j , k элементов. Таким образом, результатом ITA является рефлексивное и транзитивное отношение к множеству элементов, то есть квазипорядок элементов.
Другой алгоритм выполнения ITA был предложен Шреппом (1999) . Этот алгоритм называется Inductive ITA .
И классический ITA, и индуктивный ITA создают квазипорядок набора элементов посредством исследовательского анализа данных . Но оба метода используют разные алгоритмы построения этого квазипорядка. Для данного набора данных результирующие квазипорядки классического и индуктивного ITA обычно будут различаться.
Подробное описание алгоритмов, используемых в классическом и индуктивном ITA, можно найти в Schrepp (2003) или Schrepp (2006) [1] . В недавней статье (Sargin & Ünlü, 2009) предложены некоторые модификации алгоритма индуктивного ITA, которые улучшают способность этого метода обнаруживать правильные выводы из данных (особенно в случае более высоких коэффициентов ошибок случайных ответов).

Связь с другими методами

ITA принадлежит к группе методов анализа данных, называемых логическим анализом анкет . Булев анализ был введен Фламентом в 1976 году. ^[2] Цель булева анализа состоит в том, чтобыобнаруживать детерминированные зависимости (формулы из логической логики, соединяющие элементы, например $i\rightarrow j$ , $i\wedge j\rightarrow k$ , и $i\vee j\rightarrow k$ ) между пунктами анкеты или теста.Со времени основной работы Фламента (1976) появилось множество различных методов булева анализа.были разработаны. См., например, Van Buggenhaut and Degreef (1987) , Duquenne (1987) или Theuns (1994) .Эти методы имеют общую цель — получить детерминированные зависимости между элементами массива.анкеты на основе данных, но различаются алгоритмами достижения этой цели. Сравнение ИТАДругие методы логического анализа данных можно найти у Шреппа (2003) .

Приложения

Доступно несколько исследовательских работ, в которых описываются конкретные применения анализа дерева элементов. Хелд и Коросси (1998) анализируют последствия для ряда алгебраических задач, связанных с классическим ITA. Анализ дерева элементов также используется в ряде исследований в области социальных наук, чтобы получить представление о структуре дихотомических данных. у Барта и Круса (1973) Например, предшественник ITA используется для установления иерархического порядка элементов, описывающих социально неприемлемое поведение. В Janssens (1999) метод булева анализа используется для исследованияпроцесс интеграции меньшинств в систему ценностей доминирующей культуры. Шрепп ^[3] описывает несколько применений индуктивного ITA при анализе зависимостей между пунктами анкет по общественным наукам.

Пример приложения

Чтобы показать возможности анализа набора данных ITA, мы анализируем формулировки вопроса 4 Международной программы социальных исследований (ISSSP) за 1995 год с помощью индуктивного и классического ITA.ISSSP — это продолжающаяся ежегодная программа межнационального сотрудничества в области опросов, охватывающих важные темы исследований в области социальных наук. Программа проводит каждый год один опрос со сравнимыми вопросами в каждой из стран-участниц. Темой опроса 1995 года была национальная идентичность . Анализируем результаты по вопросу 4 для набора данных Западной Германии .Утверждение по вопросу 4 было таким:

Некоторые люди говорят, что для того, чтобы быть настоящим немцем, важны следующие вещи. Другие говорят, что они не важны. Насколько, по вашему мнению, важно каждое из следующих действий :
1. родиться в Германии
2. иметь немецкое гражданство
3. прожить в Германии большую часть жизни
4. уметь говорить по-немецки
5. быть христианином
6. уважать политические институты Германии.
7. чувствовать себя немцем

У испытуемых были варианты ответов: «Очень важно» , «Важно» , «Не очень важно» , «Совсем не важно » и «Не могу выбрать ответ на утверждения». Чтобы применить ITA к этому набору данных, мы изменили категории ответов.
«Очень важно» и «Важно» кодируются как 1. «Не очень важно» и «Совсем не важно» кодируются как 0. Невозможно выбрать , обработано как отсутствующие данные.
На следующем рисунке показаны полученные квазипорядки. $\leq _{IITA}$ от индуктивного ИТА и $\leq _{CITA}$ из классической ИТА.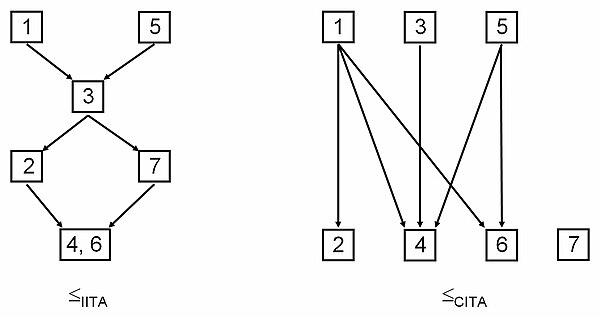

Доступное программное обеспечение

Программа ITA 2.0 реализует как классический, так и индуктивный ITA. Программа доступна по адресу [2] . Краткая документация программы доступна в [3] .

См. также

Теория ответа на предмет

Примечания

^ См. Ван Леуве (1974).
^ См. Фламент (1976).
^ См. Шрепп (2002) и Шрепп (2003).

Ссылки

Барт, В.М., и Крус, ди-джей (1973). Теоретико-упорядоченный метод определения иерархии между элементами. Образовательные и психологические измерения, 33, 291–300.
Дюкен V (1987). Концептуальные последствия между атрибутами и некоторыми свойствами представления конечных решеток. В Б. Гантере, Р. Вилле, К. Вулфе (ред.), «Вклад в концептуальный анализ: лекции на рабочей конференции по концептуальному анализу», Дармштадт, 1986, стр. 313–339. Научное издательство, Мангейм.
Фламент С (1976). Булев анализ анкеты. Овцы, Париж.
Хелд Т. и Коросси К. (1998). Анализ данных как эвристика для установления теоретически обоснованных структур элементов. Zeitschrift für Psychologie, 206, 169–188.
Янссенс, Р. (1999). Булев подход к измерению групповых процессов и отношений. Концепция интеграции как пример. Математические социальные науки, 38, 275–293.
Шрепп М (1999). Об эмпирическом построении последствий для двузначных тестовых заданий. Математические социальные науки, 38 (3), 361–375.
Шрепп, М. (2002). Исследовательский анализ эмпирических данных путем логического анализа анкет. Журнал психологии, 210/2, стр. 99–109.
Шрепп, М. (2003). Метод анализа иерархических зависимостей между пунктами анкеты. Методы психологических исследований, 19, 43–79.
Шрепп, М. (2006). ITA 2.0: программа для классического и индуктивного анализа дерева элементов. Журнал статистического программного обеспечения, Vol. 16, выпуск 10.
Шрепп, М. (2006). Свойства коэффициента корреляционного согласия: комментарий к Юнлю и Альберту (2004). Математическая социальная наука, Vol. 51, выпуск 1, 117–123.
Шрепп, М. (2007). Об оценке мер соответствия квазипорядков. Математические социальные науки Vol. 53, выпуск 2, 196–208.
Теунс П. (1994). Метод дихотомизации для булева анализа количественных данных о совместной встречаемости. В книге Дж. Фишера, Д. Ламинга (ред.), «Вклад в математическую психологию, психометрику и методологию», серия «Научная психология», стр. 173–194. Спрингер-Верлаг, Нью-Йорк.
Юнлю А. и Альберт Д. (2004). Коэффициент корреляционного согласия CA - математический анализ описательной меры согласия. Математические социальные науки, 48, 281–314.
Ван Буггенхаут Дж., Градус Э. (1987). О методах дихотомизации в булевом анализе анкет. В Э. Роскаме, Р. Сак (ред.), «Математическая психология в прогрессе», Elsevier Science Publishers BV, Северная Голландия.
Ван Леуве, JFJ (1974). Анализ дерева предметов. Голландский психологический журнал, 29, 475–484.
Саргин А. и Юнлю А. (2009). Индуктивный анализ дерева элементов: исправления, улучшения и сравнения. Математические социальные науки, 58, 376–392.

[1] См. Ван Леуве (1974).

[2] См. Фламент (1976).

[3] См. Шрепп (2002) и Шрепп (2003).

[1]

[2]

[3]