Алгоритмический вывод

Алгоритмический вывод объединяет новые разработки в методах статистического вывода , которые стали возможными благодаря мощным вычислительным устройствам, широко доступным любому аналитику данных. Краеугольными камнями в этой области являются теория вычислительного обучения , гранулярные вычисления , биоинформатика и, давным-давно, структурная вероятность ( Fraser 1966 ).Основное внимание уделяется алгоритмам, которые вычисляют статистику, лежащую в основе изучения случайного явления, а также объему данных, которые они должны использовать для получения надежных результатов. Это смещает интерес математиков от изучения законов распределения к функциональным свойствам статистики , а интерес учёных-компьютерщиков от алгоритмов обработки данных к информации, которую они обрабатывают.

Фишера

Что касается идентификации параметров закона распределения, зрелый читатель может вспомнить длительные споры середины 20-го века по поводу интерпретации их изменчивости с точки зрения фидуциального распределения ( Fisher 1956 ), структурных вероятностей ( Fraser 1966 ), априорных/апостериорных значений ( Рэмси 1925 ) и так далее. С точки зрения эпистемологии это повлекло за собой сопутствующий спор о природе вероятности : является ли это физической особенностью явлений, описываемой с помощью случайных величин , или способом синтеза данных о явлении? Выбирая последнее, Фишер определяет фидуциальный закон распределения параметров данной случайной величины, который он выводит из выборки ее спецификаций. С помощью этого закона он вычисляет, например, «вероятность того, что ц (среднее значение гауссовой переменной – примечание омера) меньше любого присвоенного значения, или вероятность того, что оно находится между любыми присвоенными значениями, или, короче говоря, его распределение вероятностей, в свете наблюдаемого образца».

Классическое решение

Фишер упорно боролся за защиту разницы и превосходства своего понятия распределения параметров по сравнению с Байеса аналогичные понятия, такие как апостериорное распределение , конструктивная вероятность Фрейзера и доверительные интервалы Неймана . В течение полувека доверительные интервалы Неймана преобладали во всех практических целях, подчеркивая феноменологическую природу вероятности. С этой точки зрения, когда вы имеете дело с гауссовой переменной, ее среднее значение μ фиксируется физическими особенностями наблюдаемого вами явления, где наблюдения являются случайными операторами, следовательно, наблюдаемые значения являются спецификациями случайной выборки . Из-за их случайности вы можете вычислить на основе конкретных интервалов выборки, содержащих фиксированное значение µ, с заданной вероятностью, которую вы обозначаете доверительностью .

Пример

Пусть X — гауссова переменная с параметрами $\mu$ и $\sigma ^{2}$ и $\{X_{1},\ldots ,X_{m}\}$ образец, взятый из него. Работа со статистикой

$S_{\mu }=\sum _{i=1}^{m}X_{i}$

и

$S_{\sigma ^{2}}=\sum _{i=1}^{m}(X_{i}-{\overline {X}})^{2},{\text{ where }}{\overline {X}}={\frac {S_{\mu }}{m}}$

является выборочным средним, мы понимаем, что

$T={\frac {S_{\mu }-m\mu }{\sqrt {S_{\sigma ^{2}}}}}{\sqrt {\frac {m-1}{m}}}={\frac {{\overline {X}}-\mu }{\sqrt {S_{\sigma ^{2}}/(m(m-1))}}}$

следует t-распределению Стьюдента ( Wilks 1962 ) с параметром (степенью свободы) m − 1, так что

$f_{T}(t)={\frac {\Gamma (m/2)}{\Gamma ((m-1)/2)}}{\frac {1}{\sqrt {\pi (m-1)}}}\left(1+{\frac {t^{2}}{m-1}}\right)^{m/2}.$

Измерение T между двумя квантилями и инвертирование его выражения как функции $\mu$ вы получаете доверительные интервалы для $\mu$.

С образцом спецификации:

$\mathbf {x} =\{7.14,6.3,3.9,6.46,0.2,2.94,4.14,4.69,6.02,1.58\}$

имея размер m = 10, вы вычисляете статистику $s_{\mu }=43.37$ и $s_{\sigma ^{2}}=46.07$и получим доверительный интервал 0,90 для $\mu$ с экстремумами (3,03, 5,65).

Вывод функций с помощью компьютера

С точки зрения моделирования весь спор выглядит как дилемма куриного яйца: либо фиксированные данные по первым и вероятностное распределение их свойств, как следствие, либо фиксированные свойства по первым и вероятностное распределение наблюдаемых данных как следствие.Классическое решение имеет одно преимущество и один недостаток. Первое особенно ценилось еще тогда, когда люди еще производили вычисления с помощью листа и карандаша. По сути, задача вычисления доверительного интервала Неймана для фиксированного параметра θ сложна: вы не знаете θ, но ищете вокруг него интервал с, возможно, очень низкой вероятностью неудачи. Аналитическое решение допускается для очень ограниченного числа теоретических случаев. И наоборот, большое количество примеров можно быстро решить приближенным способом с помощью центральной предельной теоремы с точки зрения доверительного интервала вокруг гауссова распределения – в этом преимущество. Недостаток состоит в том, что центральная предельная теорема применима, когда размер выборки достаточно велик. Следовательно, он все менее и менее применим к выборке, используемой в современных случаях вывода. Проблема не в размере выборки как таковом. Скорее, этот размер недостаточно велик из-за сложность задачи вывода.

Благодаря наличию крупных вычислительных мощностей ученые переориентировались с вывода изолированных параметров на вывод сложных функций, то есть сброс наборов сильно вложенных параметров, идентифицирующих функции. В этих случаях мы говорим об обучении функций (в терминах, например, регрессии , нейро-нечеткой системы или компьютерного обучения ) на основе высокоинформативных выборок. Первым эффектом наличия сложной структуры, связывающей данные, является уменьшение количества степеней свободы выборки , т.е. сжигание части точек выборки, так что эффективный размер выборки, который следует учитывать в центральной предельной теореме, оказывается слишком мал. Если сосредоточиться на размере выборки, обеспечивающем ограниченную ошибку обучения с заданным уровнем достоверности , то нижняя граница этого размера растет с ростом индексов сложности, таких как размерность VC или детализация класса, к которому принадлежит функция, которую мы хотим изучить.

Пример

Выборки в 1000 независимых бит достаточно, чтобы обеспечить абсолютную ошибку не более 0,081 при оценке параметра p базовой переменной Бернулли с достоверностью не менее 0,99. Один и тот же размер не может гарантировать пороговое значение меньше 0,088 с той же достоверностью 0,99, когда ошибка идентифицируется с вероятностью того, что 20-летний мужчина, живущий в Нью-Йорке, не соответствует диапазонам роста, веса и талии, наблюдаемым на 1000 Big Яблочные жители. Недостаток точности возникает из-за того, что и размерность VC, и детализация класса параллелепипедов, к которому относится наблюдаемый из диапазонов 1000 жителей, равны 6.

Общая задача обращения,

При недостаточно больших выборках подход: фиксированная выборка – случайные свойства предполагает процедуру вывода в три этапа:

1.	Механизм выборки . Он состоит из пары $(Z,g_{\boldsymbol {\theta }})$, где начальное число Z — случайная величина без неизвестных параметров, а объясняющая функция $g_{\boldsymbol {\theta }}$ представляет собой отображение функции от выборок Z к выборкам случайной величины X. Вектор параметров интересующей нас ${\boldsymbol {\theta }}$ является спецификацией случайного параметра $\mathbf {\Theta }$. Его компоненты являются параметрами X. закона распределения Теорема интегрального преобразования обеспечивает существование такого механизма для каждого (скалярного или векторного) X , когда затравочное число совпадает со случайной величиной U, равномерно распределенной в $[0,1]$. Пример. Для X соответствует распределению Парето с параметрами a и k , т.е. $F_{X}(x)=\left(1-{\frac {k}{x}}^{a}\right)I_{[k,\infty )}(x),$ механизм выборки $(U,g_{(a,k)})$ для X с начальным числом U читается: $g_{(a,k)}(u)=k(1-u)^{-{\frac {1}{a}}},$ или, что то же самое, $g_{(a,k)}(u)=ku^{-1/a}.$
2.	Основные уравнения . Фактическая связь между моделью и наблюдаемыми данными выражается в виде набора отношений между статистикой данных и неизвестными параметрами, которые являются следствием механизмов выборки. Мы называем эти отношения основными уравнениями . Вращение вокруг статистики $s=h(x_{1},\ldots ,x_{m})=h(g_{\boldsymbol {\theta }}(z_{1}),\ldots ,g_{\boldsymbol {\theta }}(z_{m}))$, общая форма основного уравнения: $s=\rho ({\boldsymbol {\theta }};z_{1},\ldots ,z_{m})$. С помощью этих отношений мы можем проверить значения параметров, которые могли бы создать выборку с наблюдаемой статистикой из определенного набора начальных значений, представляющих начальное значение выборки. Следовательно, совокупности образцов семян соответствует совокупность параметров. Чтобы обеспечить чистые свойства этой популяции, достаточно случайным образом нарисовать начальные значения и включить в основные уравнения либо достаточную статистику , либо, просто, статистику с хорошим поведением относительно параметров. Например, статистика $s_{1}=\sum _{i=1}^{m}\log x_{i}$ и $s_{2}=\min _{i=1,\ldots ,m}\{x_{i}\}$ оказываются достаточными для параметров a и k случайной величины Парето X . Благодаря (эквивалентной форме) механизму выборки $g_{(a,k)}$ мы можем читать их как $s_{1}=m\log k+1/a\sum _{i=1}^{m}\log u_{i}$ $s_{2}=\min _{i=1,\ldots ,m}\{ku_{i}^{-{\frac {1}{a}}}\},$ соответственно.
3.	Параметр популяции . Зафиксировав набор основных уравнений, вы можете сопоставить выборочные семена с параметрами либо численно с помощью начальной загрузки популяции , либо аналитически с помощью искажающего аргумента . Следовательно, из совокупности семян вы получаете совокупность параметров. Пример. Из приведенного выше основного уравнения мы можем нарисовать пару параметров: $(a,k)$, совместимого с наблюдаемой выборкой, путем решения следующей системы уравнений: $a={\frac {\sum \log u_{i}-m\log \min\{u_{i}\}}{s_{1}-m\log s_{2}}}.$ $k=\mathrm {e} ^{\frac {as_{1}-\sum \log u_{i}}{ma}}$ где $s_{1}$ и $s_{2}$ наблюдаемая статистика и $u_{1},\ldots ,u_{m}$ набор однородных семян. Перенеся в параметры вероятность (плотность), влияющую на семена, вы получите закон распределения случайных параметров А и К, совместимый с наблюдаемой вами статистикой. Совместимость обозначает параметры совместимых популяций, т.е. популяций, которые могли бы создать выборку, дающую начало наблюдаемой статистике. Формализовать это понятие можно следующим образом:

Определение

Для случайной величины и взятой из нее выборки совместимым распределением является распределение, имеющее одинаковый механизм выборки. ${\mathcal {M}}_{X}=(Z,g_{\boldsymbol {\theta }})$ X со значением ${\boldsymbol {\theta }}$ случайного параметра $\mathbf {\Theta }$ получено из основного уравнения, основанного на статистике s с хорошим поведением .

Пример

Совместная эмпирическая кумулятивная функция распределения параметров $(A,K)$ случайной величины Парето.

Кумулятивная функция распределения среднего значения M гауссовой случайной величины

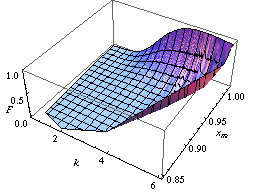
Вы можете найти закон распределения параметров Парето A и K в качестве примера реализации метода начальной загрузки населения , как на рисунке слева.

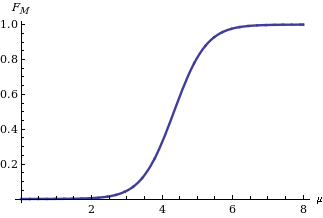
Реализуя метод скручивающего аргумента , вы получаете закон распределения $F_{M}(\mu )$ среднего значения M гауссовой переменной X на основе статистики $s_{M}=\sum _{i=1}^{m}x_{i}$ когда $\Sigma ^{2}$ известно, что он равен $\sigma ^{2}$ ( Apolloni, Malchiodi & Gaito 2006 ). Its expression is:

$F_{M}(\mu )=\Phi \left({\frac {m\mu -s_{M}}{\sigma {\sqrt {m}}}}\right),$

показано на рисунке справа, где $\Phi$ — кумулятивная функция распределения стандартного нормального распределения .

Верхний (фиолетовая кривая) и нижний (синяя кривая) экстремумы 90% доверительного интервала среднего значения M гауссовой случайной величины для фиксированной $\sigma$ и разные значения статистики s _m .

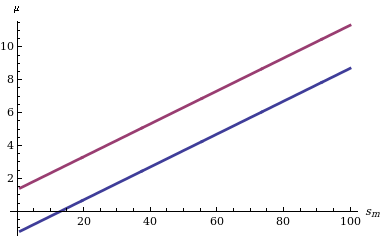
Вычислить доверительный интервал для M с учетом его функции распределения несложно: нам нужно найти только два квантиля (например, $\delta /2$ и $1-\delta /2$ квантилей в случае, если нас интересует доверительный интервал уровня δ, симметричный относительно вероятностей хвоста), как указано слева на диаграмме, показывающей поведение двух границ для разных значений статистики s _m .

Ахиллесова пята подхода Фишера заключается в совместном распределении более чем одного параметра, скажем, среднего значения и дисперсии гауссова распределения. Напротив, с помощью последнего подхода (и вышеупомянутых методов: начальной загрузки населения и скручивающего аргумента ) мы можем узнать совместное распределение многих параметров. Например, сосредоточив внимание на распределении двух или более параметров, на рисунках ниже мы сообщаем о двух доверительных областях, в которых изучаемая функция попадает с достоверностью 90%. Первое касается вероятности, с которой машина расширенных опорных векторов присваивает двоичную метку 1 точкам $(x,y)$ самолет. Две поверхности рисуются на основе набора точек выборки, которые, в свою очередь, помечены в соответствии с определенным законом распределения ( Аполлони и др., 2008 ). Последнее касается доверительной области риска рецидива рака молочной железы, рассчитанной на основе цензурированной выборки ( Аполлони, Мальчиоди и Гаито, 2006 ).

Доверительная область 90% для семейства машин опорных векторов, наделенных функцией гиперболического профиля тангенса.

Доверительная область 90% для функции риска рецидива рака молочной железы, рассчитанной на основе цензурированной выборки. $t=(9,13,>13,18,12,23,31,34,>45,48,>161),\,$ где > t обозначает цензурированное время

Ссылки

• Фрейзер, DAS (1966), «Структурная вероятность и обобщение», Biometrika , 53 (1/2): 1–9, doi : 10.2307/2334048 , JSTOR   2334048 .
• Фишер, Массачусетс (1956), Статистические методы и научные выводы , Эдинбург и Лондон: Оливер и Бойд.
• Аполлони, Б.; Мальчиоди, Д.; Гайто, С. (2006), Алгоритмический вывод в машинном обучении , Международная серия по продвинутому интеллекту, том. 5 (2-е изд.), Аделаида: Мэгилл, Advanced Knowledge International
• Аполлони, Б.; Бассис, С.; Мальчиоди, Д.; Витольд, П. (2008), Загадка гранулярных вычислений , Исследования в области вычислительного интеллекта, том. 138, Берлин: Springer, ISBN.  9783540798637
• Рэмси, Ф. П. (1925), «Основы математики», Труды Лондонского математического общества : 338–384, doi : 10.1112/plms/s2-25.1.338 .
• Уилкс, СС (1962), Математическая статистика , Публикации Wiley по статистике, Нью-Йорк: Джон Уайли