Принцип Шаймпфлюга

Принцип Шаймпфлюга — это описание геометрической взаимосвязи между ориентацией плоскости фокуса , плоскостью линзы и плоскостью изображения оптической системы (например, камеры), когда плоскость линзы не параллельна плоскости изображения. Это применимо к использованию некоторых движений камеры на камере обзора . Этот же принцип используется в пахиметрии роговицы , картировании топографии роговицы, выполняемой перед рефракционной хирургией глаза , такой как LASIK , и используемой для раннего выявления кератоконуса . Принцип назван в честь капитана австрийской армии Теодора Шаймпфлюга , который использовал его при разработке систематического метода и аппарата для исправления перспективных искажений на аэрофотоснимках , хотя сам капитан Шаймпфлюг приписывает это правило Жюлю Карпантье , тем самым делая его примером закона эпонимии Стиглера. .

Описание

Рисунок 1. В обычной камере, когда объект не параллелен плоскости изображения, в фокусе находится только небольшая область.

Рисунок 2. Углы принципа Шаймпфлюга на примере фотообъектива

Рисунок 4. Расстояние и угол оси вращения PoF.

Обычно плоскости объектива и изображения (пленки или сенсора) камеры параллельны, а плоскость фокуса (PoF) параллельна плоскостям объектива и изображения. Если плоский объект (например, сторона здания) также параллелен плоскости изображения, он может совпадать с PoF, и весь объект может быть визуализирован четко. Если плоскость объекта не параллельна плоскости изображения, она будет в фокусе только вдоль линии, где она пересекает PoF, как показано на рисунке 1.

Но когда линза наклонена относительно плоскости изображения, косая касательная, выходящая из плоскости изображения , и другая, выходящая из плоскости линзы, встречаются на линии, через которую также проходит PoF, как показано на рисунке 2. При этом условии плоский объект, не параллельный плоскости изображения, может быть полностью в фокусе. Хотя многие фотографы не знали или не знали о точном геометрическом соотношении между PoF, плоскостью объектива и плоскостью пленки, поворот и наклон объектива для поворота и наклона PoF практиковались с середины 19 века. Но когда Карпентье и Шаймпфлюг захотели создать оборудование для автоматизации процесса, им нужно было найти геометрическую зависимость.

Шаймпфлюг (1904) упомянул эту концепцию в своем британском патенте; Карпентье (1901) также описал эту концепцию в более раннем британском патенте на фотоувеличитель с коррекцией перспективы . Эту концепцию можно вывести из теоремы проективной геометрии Дезарга Жерара ; этот принцип также легко выводится из простых геометрических соображений и применения формулы Гаусса для тонкой линзы , как показано в разделе « Доказательство принципа Шаймпфлюга» .

Изменение плоскости фокуса

Если плоскости объектива и изображения не параллельны, регулировка фокуса ^[а] вращает PoF, а не просто смещает его вдоль оси объектива. линзы Ось вращения — это пересечение передней фокальной плоскости и плоскости, проходящей через центр линзы, параллельной плоскости изображения, как показано на рисунке 3. Когда плоскость изображения перемещается от IP ₁ к IP ₂ , PoF вращается. вокруг оси G из положения PoF ₁ в положение PoF ₂ ; «линия Шаймпфлюга» перемещается из положения S1 _в положение _S2 . Оси вращения давали много разных названий: «противоось» (Scheimpflug 1904), «шарнирная линия» (Merklinger 1996) и «точка поворота» (Wheeler).

См. рисунок 4; если линза с фокусным расстоянием f наклонена на угол θ относительно плоскости изображения, расстояние J ^[б] от центра линзы до оси G определяется выражением

J={\frac {f}{\sin \theta }}.

Если v' — расстояние вдоль луча зрения от плоскости изображения до центра линзы, угол ψ между плоскостью изображения и PoF определяется выражением ^[с]

\tan \psi ={\frac {v'}{v'\cos \theta -f}}\sin \theta .

Аналогично, на стороне объекта линзы, если u' — это расстояние вдоль луча зрения от центра линзы до PoF, угол ψ определяется выражением

\tan \psi ={\frac {u'}{f}}\sin \theta .

Угол ψ увеличивается с увеличением расстояния фокусировки; когда фокус находится на бесконечности, PoF перпендикулярен плоскости изображения при любом ненулевом значении наклона. Расстояния u' и v' вдоль луча зрения не до объекта и изображения, являются расстояниями u и v используемыми в формуле тонкой линзы.

{\frac {1}{u}}+{\frac {1}{v}}={\frac {1}{f}},

где расстояния перпендикулярны плоскости линзы. Расстояния u и v связаны с расстояниями прямой видимости соотношением и = и' потому что θ и v равно v' потому знак что θ .

Для по существу плоского объекта, такого как дорога, простирающаяся на многие мили от камеры на ровной местности, можно установить наклон так, чтобы ось G поместилась в плоскость объекта, а затем отрегулировать фокус так, чтобы повернуть PoF так, чтобы он совпадал с предметная плоскость. Весь объект может быть в фокусе, даже если он не параллелен плоскости изображения.

Плоскость фокусировки также можно повернуть так, чтобы она не совпадала с плоскостью объекта съемки и чтобы в фокусе находилась только небольшая часть объекта. Этот метод иногда называют «анти-Шеймпфлюгом», хотя на самом деле он основан на принципе Шаймпфлюга.

Вращение плоскости фокуса можно осуществить путем вращения либо плоскости линзы, либо плоскости изображения. Вращение объектива (как при настройке переднего стандарта на камере обзора ) не меняет линейную перспективу. ^[д] для плоского объекта, например фасада здания, но требуется объектив с большим кругом изображения для предотвращения виньетирования . Вращение плоскости изображения (например, путем регулировки заднего или заднего стандарта на камере обзора) изменяет перспективу (например, стороны здания сходятся), но работает с объективом, имеющим меньший круг изображения. Вращение линзы или назад вокруг горизонтальной оси обычно называют наклоном , а вращение вокруг вертикальной оси обычно называют поворотом .

Движения камеры

Наклон и поворот — это движения, доступные на большинстве камер обзора , часто как на передних, так и на задних стандартах, а также на некоторых камерах малого и среднего формата , использующих специальные объективы, которые частично имитируют движения камеры обзора. Такие объективы часто называют объективами с наклоном-шифтом или объективами с « управлением перспективой ». ^[и] Для некоторых моделей камер имеются адаптеры, которые позволяют перемещать некоторые обычные объективы производителя, а грубое приближение можно получить с помощью таких приспособлений, как « Lensbaby » или « фрилинзинг ».

Глубина резкости

Когда плоскости объектива и изображения параллельны, глубина резкости (DoF) простирается между параллельными плоскостями по обе стороны от плоскости фокуса. Когда применяется принцип Шаймпфлюга, степень свободы приобретает клиновидную форму (Merklinger 1996, 32; Tillmanns 1997, 71). ^[ф] с вершиной клина на оси вращения PoF, ^[г] как показано на рисунке 5. Степень резкости равна нулю на вершине, остается небольшой на краю поля зрения объектива и увеличивается по мере удаления от камеры. Неглубокая глубина резкости рядом с камерой требует тщательного позиционирования PoF, если близлежащие объекты должны отображаться четко.

В плоскости, параллельной плоскости изображения, степень резкости равномерно распределяется выше и ниже PoF; на рисунке 5 расстояния y _n и y _f на плоскости VP равны. Это распределение может быть полезно при определении лучшей позиции для PoF; Если сцена включает в себя удаленный высокий объект, лучшее соответствие глубины резкости сцене часто достигается за счет прохождения PoF через вертикальную среднюю точку этого объекта. Однако угловая глубина резкости неравномерно распределена по PoF.

Расстояния y _n и y _f определяются формулами (Merklinger 1996, 126)

y_{x}={\frac {f}{v'}}{\frac {u'}{u}}_{\mathrm {h} }J\,,

где f — фокусное расстояние объектива, v’ и u’ — расстояния между изображением и объектом, параллельные лучу зрения, u _h — гиперфокальное расстояние , а J — расстояние от центра линзы до оси вращения PoF. Решив уравнение на стороне изображения для tan ψ для v′ и подставив v′ и u _h в приведенное выше уравнение, ^[час] значения могут быть заданы эквивалентно

y_{x}={\frac {Nc}{f}}\left({\frac {1}{\tan \theta }}-{\frac {1}{\tan \psi }}\right)u'\,,

где N объектива — f -число , а c — круг нерезкости . На большом расстоянии фокусировки (эквивалентном большому углу между PoF и плоскостью изображения) v′ ≈ f и (Merklinger 1996, 48) ^[я]

y_{x}\approx {\frac {u'}{u}}_{\mathrm {h} }J\,,

или

y_{x}\approx {\frac {Nc}{f}}{\frac {u'}{\tan \theta }}\,.

Таким образом, на гиперфокальном расстоянии глубина резкости в плоскости, параллельной плоскости изображения, простирается на расстояние J по обе стороны от точки зрения.

Для некоторых объектов, таких как пейзажи, клиновидная глубина резкости хорошо подходит для сцены, а удовлетворительная резкость часто может быть достигнута с меньшим числом f объектива (большая диафрагма ), чем требовалось бы, если бы PoF был параллелен плоскость изображения.

Селективный фокус

Область резкости также можно сделать очень маленькой, используя большой наклон и маленькое число f . Например, при наклоне объектива 90 мм на 8° для малоформатной камеры общая вертикальная глубина резкости на гиперфокальном расстоянии составляет примерно ^[Дж]

2J=2{\frac {f}{\sin \theta }}=2\times {\frac {90{\text{ mm}}}{\sin 8^{\circ }}}=1293{\text{ mm}}\,.

При диафрагме f /2,8 и круге нерезкости 0,03 мм это происходит на расстоянии u' примерно

{\frac {f^{2}}{Nc}}={\frac {90^{2}}{2.8\times 0.03}}=96.4{\text{ m}}\,.

Конечно, наклон также влияет на положение PoF, поэтому, если наклон выбран для минимизации области резкости, PoF нельзя настроить так, чтобы он проходил через более чем одну произвольно выбранную точку. Если PoF должен проходить через более чем одну произвольную точку, наклон и фокус фиксированы, а число f объектива является единственным доступным элементом управления для регулировки резкости.

Вывод формул

Доказательство принципа Шаймпфлюга

Рис. 6. Плоскость объекта, наклоненная к плоскости линзы

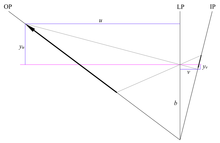
В двухмерном представлении плоскость объекта, наклоненная к линзеплоскость – это линия, описываемая

y_{u}=au+b

.

Согласно оптическому соглашению, расстояния как до объекта, так и до изображения для реальных изображений положительны, так что на рисунке 6 расстояние до объекта u увеличивается слева от плоскости линзы LP; вертикальная ось использует обычное декартово соглашение со значениями выше оптической оси положительными, а значения ниже оптической оси отрицательными.

Связь между расстоянием до объекта u , расстоянием изображения v и фокусным расстоянием линзы f определяется уравнением тонкой линзы

{\frac {1}{u}}+{\frac {1}{v}}={\frac {1}{f}}\,;

решение за тебя дает

u={\frac {vf}{v-f}}\,,

так что

y_{u}=a\,{\frac {vf}{v-f}}+b

.

Увеличение m — это отношение высоты изображения y _v к высоте объекта y _u :

m={\frac {y_{v}}{y_{u}}}\,;

y _u и y _v имеют противоположный смысл, поэтому увеличение отрицательное, что указывает на перевернутое изображение. Из подобных треугольников на рисунке 6 увеличение также связывает расстояния между изображением и объектом, так что

m=-{\frac {v}{u}}=-{\frac {v-f}{f}}

.

На стороне изображения объектива

{\begin{aligned}y_{v}&=my_{u}\\&=-{\frac {v-f}{f}}\left(a\,{\frac {vf}{v-f}}+b\right)\\&=-\left(av+{\frac {v}{f}}b-b\right)\,,\end{aligned}}

предоставление

y_{v}=-\left(a+{\frac {b}{f}}\right)v+b

.

Местом фокуса наклонной объектной плоскости является плоскость; в двумерном представлении точка пересечения оси Y такая же, как и для линии, описывающей плоскость объекта, поэтому плоскость объекта, плоскость линзы и плоскость изображения имеют общее пересечение.

Аналогичное доказательство дает Лармор (1965, 171–173).

Угол PoF с плоскостью изображения

Судя по рисунку 7,

\tan \psi ={\frac {u'+v'}{S}}\,,

где u' и v' — расстояния до объекта и изображения вдоль луча зрения, а S — расстояние от луча зрения до пересечения Шаймпфлюга в точке S. Опять же из рисунка 7:

\tan \theta ={\frac {v'}{S}}\,;

объединение двух предыдущих уравнений дает

\tan \psi ={\frac {u'+v'}{v'}}\tan \theta =\left({\frac {u'}{v'}}+1\right)\tan \theta \,.

Из уравнения тонкой линзы

{\frac {1}{u}}+{\frac {1}{v}}={\frac {1}{u'\cos \theta }}+{\frac {1}{v'\cos \theta }}={\frac {1}{f}}\,.

Решение для u' дает

u'={\frac {v'f}{v'\cos \theta -f}}\,;

подстановка этого результата в уравнение для tan ψ дает

\tan \psi =\left({\frac {f}{v'\cos \theta -f}}+1\right)\tan \theta ={\frac {f+v'\cos \theta -f}{v'\cos \theta -f}}\tan \theta \,,

или

\tan \psi ={\frac {v'}{v'\cos \theta -f}}\sin \theta \,.

Аналогичным образом уравнение тонкой линзы можно решить для v′ и результат подставить в уравнение для tan ψ, чтобы получить соотношение между объектом и объектом.

\tan \psi ={\frac {u'}{f}}\sin \theta \,.

отмечая, что

{\frac {u'}{f}}={\frac {u}{f}}{\frac {1}{\cos \theta }}={\frac {m+1}{m}}{\frac {1}{\cos \theta }}\,,

Связь между ψ и θ может быть выражена через увеличение m объекта на луче зрения:

\tan \psi ={\frac {m+1}{m}}\tan \theta \,.

Доказательство «правила шарнира»

Судя по рисунку 7,

\tan \psi ={\frac {u'}{J}}\,;

объединение с предыдущим результатом для стороны объекта и исключение ψ дает

\sin \theta ={\frac {f}{J}}\,.

Опять же из рисунка 7,

\sin \theta ={\frac {d}{J}}\,,

таким образом, расстояние d — это фокусное расстояние объектива f , а точка G находится на пересечении передней фокальной плоскости объектива с линией, параллельной плоскости изображения. Расстояние J зависит только от наклона объектива и фокусного расстояния объектива; в частности, на него не влияют изменения фокуса. Судя по рисунку 7,

\tan \theta ={\frac {v'}{S}}\,,

поэтому расстояние до пересечения Шаймпфлюга в точке S меняется при изменении фокуса. Таким образом, PoF вращается вокруг оси G при настройке фокуса.

Примечания

^ Строго говоря, ось вращения PoF остается фиксированной только тогда, когда фокус регулируется путем перемещения камеры назад, как на камере обзора. При фокусировке путем перемещения объектива происходит небольшое движение оси вращения, но за исключением очень малых расстояний от камеры до объекта, движение обычно незначительное.
^ Символ J для обозначения расстояния от центра линзы до оси вращения PoF был введен Мерклингером (1996) и, по-видимому, не имеет особого значения.
^ Мерклингер (1996, 24) дает формулу для угла плоскости фокуса как
${\frac {v'}{f}}=\sin \theta \left[{\frac {1}{\tan \left(\psi -\theta \right)}}+{\frac {1}{\tan \theta }}\right]\,;$
применяя формулу разности углов касательной и перестановки, ее можно преобразовать к виду, приведенному в этой статье.
^ Строго говоря, сохранение плоскости изображения параллельно плоскому объекту позволяет сохранить перспективу этого объекта только в том случае, если линза имеет симметричную конструкцию, т. е. входной и выходной зрачки совпадают с узловыми плоскостями . Большинство объективов для камер обзора почти симметричны, но это не всегда так с объективами с наклоном/сдвигом, используемыми в камерах малого и среднего формата, особенно с широкоугольными объективами конструкции ретрофокусной . Если ретрофокусный или телеобъектив наклонен, возможно, потребуется отрегулировать угол задней камеры, чтобы сохранить перспективу.
^ Самые ранние объективы Nikon с контролем перспективы имели только сдвиг, отсюда и обозначение «ПК»; Объективы Nikon PC, представленные с 1999 года, также имеют функцию наклона, но сохраняют прежнее обозначение.
^ Когда плоскость объектива не параллельна плоскости изображения, пятна размытия представляют собой эллипсы, а не круги, а пределы глубины резкости не совсем плоские. Данных о восприятии человеком эллиптических, а не круговых размытий мало, но принятие главной оси эллипса в качестве определяющего измерения, возможно, является наихудшим случаем. Используя это предположение, Роберт Уиллер исследует влияние эллиптических пятен размытия на пределы глубины резкости для наклоненного объектива в своих «Заметках о геометрии камеры обзора»; он заключает, что в типичных приложениях эффект незначителен и что предположение о плоских пределах глубины резкости разумно. Однако его анализ рассматривает только точки в вертикальной плоскости, проходящей через центр линзы. Леонард Эвенс исследует эффект эллиптического размытия в любой произвольной точке плоскости изображения и приходит к выводу, что в большинстве случаев ошибка, связанная с предположением о плоских пределах глубины резкости, незначительна.
^ Тиллманнс указывает, что такое поведение было обнаружено во время разработки камеры Sinar e (выпущенной в 1988 году), и что до этого считалось, что клин ГРИП простирается до линии пересечения плоскостей объекта, объектива и изображения. Он не обсуждает вращение PoF вокруг вершины клина DoF.
^ Мерклингер использует приближение u _h ≈ f ²/ N c , чтобы вывести его формулу, поэтому замена здесь точная.
^ Строго говоря, когда фокусное расстояние приближается к бесконечности, v ' cos θ → f ; раз следовательно, приближенные формулы отличаются в cos θ . При малых значениях cos θ θ ≈ 1 , поэтому разница незначительна. При больших значениях наклона, что иногда может потребоваться для широкоформатной камеры, ошибка становится больше, и либо точную формулу, либо приблизительную формулу в терминах tan θ . следует использовать
^ В примере здесь используется приближение Мерклингера. Для малых значений наклона sin θ ≈ tan θ , поэтому ошибка минимальна; для больших значений наклона знаменатель должен быть tan θ .

Ссылки

Карпентье, Жюль. 1901. Улучшения в увеличении камер. Патент Великобритании № 1139. Подан 17 января 1901 г., выдан 2 ноября 1901 г. Доступен для скачивания ( PDF ).
Лармор, Льюис. 1965. Введение в принципы фотографии . Нью-Йорк: Dover Publications, Inc.
Мерклингер, Гарольд М. 1996. Фокусировка камеры обзора . Бедфорд, Новая Шотландия: Seaboard Printing Limited. ISBN 0-9695025-2-4 . Доступно для скачивания (PDF).
Шаймпфлюг, Теодор. 1904. Усовершенствованный метод и устройство для систематического изменения или искажения плоских изображений и изображений с помощью линз и зеркал для фотографии и для других целей. Патент Великобритании № 1196. Подан 16 января 1904 г., выдан 12 мая 1904 г. Доступен для скачивания (PDF).
Тильманс, Урс. 1997. Творческий большой формат: основы и приложения . 2-е изд. Фойертален, Швейцария: Sinar AG. ISBN 3-7231-0030-9
Стегер, Карстен (2017). «Комплексная и универсальная модель камеры для камер с наклонными объективами» . Международный журнал компьютерного зрения . 123 : 121–159. дои : 10.1007/s11263-016-0964-8 .

Внешние ссылки

Посмотреть геометрию камеры (PDF) Леонарда Эвенса. Анализ влияния эллиптических пятен размытия на глубину резкости
Глубина резкости наклоненной линзы (PDF), автор Леонард Эвенс. Более практичное и доступное описание просмотра геометрии камеры.
«Как сфокусировать камеру обзора» , Куанг-Туан Луонг. Включает обсуждение того, как установить плоскость фокуса.
Принцип Шаймпфлюга Гарольда Мерклингера
Приложение к фокусировке камеры обзора (PDF), Гарольд Мерклингер
Односторонняя видеосъемка Шаймпфлюга в реальном времени для изучения динамики аккомодации в глазах человека (PDF), автор: Рам Субраманиан
Примечания к просмотру геометрии камеры (PDF) Роберта Уиллера
Наклонно-шифт-объективы : предназначены для наклонно-шифтовых объективов малого формата, но принципы применимы к любому формату.

[1] Строго говоря, ось вращения PoF остается фиксированной только тогда, когда фокус регулируется путем перемещения камеры назад, как на камере обзора. При фокусировке путем перемещения объектива происходит небольшое движение оси вращения, но за исключением очень малых расстояний от камеры до объекта, движение обычно незначительное.

[2] Символ J для обозначения расстояния от центра линзы до оси вращения PoF был введен Мерклингером (1996) и, по-видимому, не имеет особого значения.

[3] Мерклингер (1996, 24) дает формулу для угла плоскости фокуса как
${\frac {v'}{f}}=\sin \theta \left[{\frac {1}{\tan \left(\psi -\theta \right)}}+{\frac {1}{\tan \theta }}\right]\,;$
применяя формулу разности углов касательной и перестановки, ее можно преобразовать к виду, приведенному в этой статье.

[4] Строго говоря, сохранение плоскости изображения параллельно плоскому объекту позволяет сохранить перспективу этого объекта только в том случае, если линза имеет симметричную конструкцию, т. е. входной и выходной зрачки совпадают с узловыми плоскостями . Большинство объективов для камер обзора почти симметричны, но это не всегда так с объективами с наклоном/сдвигом, используемыми в камерах малого и среднего формата, особенно с широкоугольными объективами конструкции ретрофокусной . Если ретрофокусный или телеобъектив наклонен, возможно, потребуется отрегулировать угол задней камеры, чтобы сохранить перспективу.

[5] Самые ранние объективы Nikon с контролем перспективы имели только сдвиг, отсюда и обозначение «ПК»; Объективы Nikon PC, представленные с 1999 года, также имеют функцию наклона, но сохраняют прежнее обозначение.

[6] Когда плоскость объектива не параллельна плоскости изображения, пятна размытия представляют собой эллипсы, а не круги, а пределы глубины резкости не совсем плоские. Данных о восприятии человеком эллиптических, а не круговых размытий мало, но принятие главной оси эллипса в качестве определяющего измерения, возможно, является наихудшим случаем. Используя это предположение, Роберт Уиллер исследует влияние эллиптических пятен размытия на пределы глубины резкости для наклоненного объектива в своих «Заметках о геометрии камеры обзора»; он заключает, что в типичных приложениях эффект незначителен и что предположение о плоских пределах глубины резкости разумно. Однако его анализ рассматривает только точки в вертикальной плоскости, проходящей через центр линзы. Леонард Эвенс исследует эффект эллиптического размытия в любой произвольной точке плоскости изображения и приходит к выводу, что в большинстве случаев ошибка, связанная с предположением о плоских пределах глубины резкости, незначительна.

[7] Тиллманнс указывает, что такое поведение было обнаружено во время разработки камеры Sinar e (выпущенной в 1988 году), и что до этого считалось, что клин ГРИП простирается до линии пересечения плоскостей объекта, объектива и изображения. Он не обсуждает вращение PoF вокруг вершины клина DoF.

[8] Мерклингер использует приближение u _h ≈ f ²/ N c , чтобы вывести его формулу, поэтому замена здесь точная.

[9] Строго говоря, когда фокусное расстояние приближается к бесконечности, v ' cos θ → f ; раз следовательно, приближенные формулы отличаются в cos θ . При малых значениях cos θ θ ≈ 1 , поэтому разница незначительна. При больших значениях наклона, что иногда может потребоваться для широкоформатной камеры, ошибка становится больше, и либо точную формулу, либо приблизительную формулу в терминах tan θ . следует использовать

[10] В примере здесь используется приближение Мерклингера. Для малых значений наклона sin θ ≈ tan θ , поэтому ошибка минимальна; для больших значений наклона знаменатель должен быть tan θ .

[а]

[б]

[с]

[д]

[и]

[ф]

[г]

[час]

[я]

[Дж]