f-число

Чтобы узнать о других значениях, см. F-число (значения) .

Схема уменьшения диафрагмы , то есть увеличения диафрагменного числа с шагом в один стоп; каждая апертура имеет площадь сбора света вдвое меньшую, чем предыдущая.

Число f — это мера светосилы оптической системы, например объектива камеры . системы Оно рассчитывается путем деления фокусного расстояния на диаметр входного зрачка («светлая апертура »). Число f также известно как фокусное соотношение , f-отношение или диафрагменное число , и оно играет ключевую роль в определении глубины резкости , дифракции и экспозиции фотографии. Число f безразмерно в нижнем регистре и обычно выражается с помощью зацепленной f в формате f / N , где N — f-число.

Число f также известно как обратное относительное отверстие , поскольку оно является обратной величиной относительного отверстия , определяемого как диаметр апертуры, разделенный на фокусное расстояние. Относительное отверстие показывает, сколько света может пройти через объектив при данном фокусном расстоянии. Меньшее число f означает большее относительное отверстие и больше света, попадающего в систему, тогда как более высокое число f означает меньшее относительное отверстие и меньше света, попадающего в систему. Число f связано с числовой апертурой (NA) системы, которая измеряет диапазон углов, под которыми свет может проникать в систему или выходить из нее. Числовая апертура учитывает показатель преломления среды, в которой работает система, а число f — нет.

Обозначения

F-число N определяется как:

$$N={\frac {f}{D}}\$$

где $f$ — фокусное расстояние , а $D$ — диаметр входного зрачка ( эффективная апертура ). Принято писать f-числа перед " f / ", что образует математическое выражение диаметра входного зрачка через $f$ и Н. ​ Например, если фокусное расстояние объектива составляет 10 мм, а диаметр его входного зрачка — 5 мм, число f будет равно 2. Это будет выражаться как « f / 2" в системе линз. Диаметр апертуры был бы равен $f/2$.

Большинство объективов имеют регулируемую диафрагму , которая меняет размер диафрагмы и , следовательно, размер входного зрачка. Это позволяет пользователю изменять число f по мере необходимости. Диаметр входного зрачка не обязательно равен диаметру диафрагмы из-за увеличивающего эффекта линз перед диафрагмой.

Игнорируя различия в эффективности светопропускания, объектив с большим числом f проецирует более темные изображения. Яркость проецируемого изображения ( освещенность ) относительно яркости сцены в поле зрения объектива ( освещенность ) уменьшается пропорционально квадрату числа f. Фокусное расстояние 100 мм. Объектив f / 4 имеет диаметр входного зрачка 25 мм. Фокусное расстояние 100 мм. Объектив f / 2 имеет диаметр входного зрачка 50 мм. Поскольку площадь пропорциональна квадрату диаметра зрачка, количество света, пропускаемое Объектив с диафрагмой f / 2 в четыре раза больше, чем у объектива объектив f / 4. Чтобы получить такую ​​же фотографическую экспозицию , время экспозиции необходимо уменьшить в четыре раза.

Фокусное расстояние 200 мм. Объектив f / 4 имеет диаметр входного зрачка 50 мм. Входной зрачок объектива с фокусным расстоянием 200 мм в четыре раза больше площади, чем у объектива с фокусным расстоянием 100 мм. Входной зрачок объектива f / 4 и, таким образом, собирает в четыре раза больше света от каждого объекта в поле зрения объектива. Но по сравнению с объективом 100 мм объектив 200 мм проецирует изображение каждого объекта в два раза выше и в два раза шире, охватывая в четыре раза большую площадь, и поэтому обе линзы создают одинаковую освещенность в фокальной плоскости при изображении сцены. заданная яркость.

Т -стоп — это число f, корректируемое с учетом эффективности светопропускания.

диафрагмы

Canon 7 с объективом 50 мм, способным f / 0,95

Объектив 35 мм, установленный на f / 11, на что указывает белая точка над шкалой диафрагмы на кольце диафрагмы. Этот объектив имеет диапазон диафрагмы f / 2 до ф / 22.

Слово «стоп» иногда сбивает с толку из-за его множества значений. Остановкой может быть физический объект: непрозрачная часть оптической системы, блокирующая определенные лучи. — Стопор диафрагмы это настройка диафрагмы, которая ограничивает яркость изображения путем ограничения размера входного зрачка, а стопор поля — это ограничитель, предназначенный для исключения света, который находится за пределами желаемого поля зрения и может вызвать блики или другие проблемы, если не остановился.

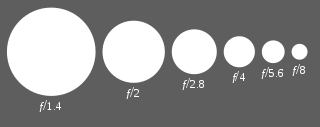
В фотографии стопы также являются единицей измерения соотношения света или экспозиции: каждая добавленная стопа означает коэффициент в два раза, а каждая вычтенная стопа означает коэффициент в два раза. Единица измерения одной остановки также известна как единица EV ( величина экспозиции ). В камере настройка диафрагмы традиционно регулируется дискретными шагами, известными как диафрагмы . Каждая « стоп » отмечена соответствующим числом f и представляет собой уменьшение вдвое интенсивности света по сравнению с предыдущей остановкой. Это соответствует уменьшению диаметров зрачка и апертуры в 1/ √ 2 раза или примерно 0,7071 и, следовательно, уменьшению площади зрачка вдвое.

В большинстве современных объективов используется стандартная шкала диафрагмы, которая представляет собой приблизительно геометрическую последовательность чисел, соответствующую последовательности степеней квадратного корня из 2 : ж / 1, f / 1,4, ф / 2, f / 2,8, f / 4, f / 5,6, f / 8, ф / 11, ф / 16, ф / 22, ф / 32, ф / 45, ф / 64, ф / 90, f / 128 и т. д. Каждый элемент в последовательности на одну ступень ниже, чем элемент слева от него, и на одну ступень выше, чем элемент справа. Значения коэффициентов округляются до этих конкретных условных чисел, чтобы их было легче запомнить и записать.Приведенная выше последовательность получается путем аппроксимации следующей точной геометрической последовательности:

$$f/1={\frac {f}{({\sqrt {2}})^{0}}},\ f/1.4={\frac {f}{({\sqrt {2}})^{1}}},\ f/2={\frac {f}{({\sqrt {2}})^{2}}},\ f/2.8={\frac {f}{({\sqrt {2}})^{3}}},\ \ldots$$

Точно так же, как одна диафрагма соответствует двукратной интенсивности света, выдержки устроены так, что каждая настройка отличается по продолжительности примерно в два раза от соседней. Открытие объектива на одну ступень позволяет за определенный период времени на пленку попасть в два раза больше света. Следовательно, чтобы получить ту же экспозицию при этой большей диафрагме, что и при предыдущей диафрагме, затвор должен быть открыт вдвое дольше (т. е. на удвоенную скорость). Пленка будет одинаково реагировать на эти равные количества света, поскольку она обладает свойством взаимности . Это менее верно для чрезвычайно длинных или коротких выдержек, когда взаимность нарушается . Диафрагма, выдержка и чувствительность пленки связаны между собой: для постоянной яркости сцены удвоение площади диафрагмы (одна ступень), уменьшение вдвое выдержки (удвоение времени открытия) или использование пленки с удвоенной чувствительностью оказывают одинаковый эффект на экспонированное изображение. Для всех практических целей исключительная точность не требуется (механическая выдержка, как известно, была неточной из-за изменения износа и смазки, что не влияло на экспозицию). Несущественно, что площадь диафрагмы и выдержка не изменяются ровно в два раза.

Фотографы иногда выражают другие соотношения экспозиции через «ступени». Не обращая внимания на маркировку числа f, диафрагмы составляют логарифмическую шкалу интенсивности экспозиции. Учитывая эту интерпретацию, можно затем подумать о том, чтобы сделать полшага по этой шкале, чтобы разница экспозиции составила «полстопа».

Дробные стопы

Компьютерное моделирование, показывающее эффекты изменения диафрагмы камеры в полустопах (слева) и от нуля до бесконечности (справа).

Большинство камер двадцатого века имели бесступенчатую апертуру с использованием ирисовой диафрагмы с маркировкой каждой точки. Диафрагма с остановкой по щелчку стала широко использоваться в 1960-х годах; шкала диафрагмы обычно имела остановку щелчка на каждой целой и полуступени.

В современных камерах, особенно когда диафрагма установлена ​​на корпусе камеры, число f часто делится более точно, чем шаги в одну ступень. Шаги в одну треть стопа ( 1/3 EV) являются наиболее распространенными, поскольку соответствуют системе светочувствительности пленки ISO . В некоторых камерах используются полустопные шаги. Обычно точки отмечены, а промежуточные положения щелкают, но не отмечаются. Например, апертура, которая на одну треть стопа меньше, чем f / 2.8 есть f / 3.2, на две трети меньше f / 3.5, а на целый стоп меньше f / 4. Следующие несколько ступеней диафрагмы в этой последовательности:

$$f/4.5,\ f/5,\ f/5.6,\ f/6.3,\ f/7.1,\ f/8,\ \ldots$$

Чтобы рассчитать шаги при полной остановке (1 EV), можно использовать

$$({\sqrt {2}})^{0},\ ({\sqrt {2}})^{1},\ ({\sqrt {2}})^{2},\ ({\sqrt {2}})^{3},\ ({\sqrt {2}})^{4},\ \ldots$$

Шаги в полстопа ( 1 ⁄ EV ) серия будет

$$({\sqrt {2}})^{\frac {0}{2}},\ ({\sqrt {2}})^{\frac {1}{2}},\ ({\sqrt {2}})^{\frac {2}{2}},\ ({\sqrt {2}})^{\frac {3}{2}},\ ({\sqrt {2}})^{\frac {4}{2}},\ \ldots$$

Шаги на третьей остановке ( 1 ⁄ EV ) серия будет

$$({\sqrt {2}})^{\frac {0}{3}},\ ({\sqrt {2}})^{\frac {1}{3}},\ ({\sqrt {2}})^{\frac {2}{3}},\ ({\sqrt {2}})^{\frac {3}{3}},\ ({\sqrt {2}})^{\frac {4}{3}},\ \ldots$$

Как и в более ранних стандартах светочувствительности пленки DIN и ASA, чувствительность ISO определяется только с шагом в одну треть ступени, а выдержки цифровых камер обычно находятся в той же шкале в обратных секундах. Часть диапазона ISO представляет собой последовательность

$$\ldots 16/13^{\circ },\ 20/14^{\circ },\ 25/15^{\circ },\ 32/16^{\circ },\ 40/17^{\circ },\ 50/18^{\circ },\ 64/19^{\circ },\ 80/20^{\circ },\ 100/21^{\circ },\ 125/22^{\circ },\ \ldots$$

тогда как выдержки в обратных секундах имеют несколько условных отличий в своих цифрах ( 1 ⁄ 15 , 1 ⁄ 30 и 1 ⁄ секунды вместо 1 ⁄ 16 , 1 ⁄ 32 и 1 ⁄ 64 ).

На практике максимальная светосила объектива часто не равна целой степени √ 2 (т. е. √ 2 в степени целого числа), и в этом случае она обычно на половину или треть стопа выше или ниже целой степени √. 2 .

Современные сменные объективы с электронным управлением, например те, которые используются в зеркальных фотоаппаратах, имеют диафрагму, указанную внутри. с шагом 1 ⁄ 8 ступени, поэтому камеры Настройки 1 ⁄ ступени аппроксимируются ближайшим 1/8 на ступени . Настройка объектива

Стандартная шкала диафрагменного числа с полной остановкой

Включая значение диафрагмы ВЫКЛ:

$$N={\sqrt {2^{\text{AV}}}}$$

Обычные и расчетные числа f, серия с точкой:

ИЗ	−2	−1	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Н	0.5	0.7	1.0	1.4	2	2.8	4	5.6	8	11	16	22	32	45	64	90	128	180	256
рассчитанный	0.5	0.707...	1.0	1.414...	2.0	2.828...	4.0	5.657...	8.0	11.31...	16.0	22.62...	32.0	45.25...	64.0	90.51...	128.0	181.02...	256.0

Типичная шкала числа f с полуступенью

ИЗ	−1	− 1 ⁄ 2	0	1 ⁄ 2	1	1 + 1 ⁄ 2	2	2 + 1 ⁄ 2	3	3 + 1 ⁄ 2	4	4 + 1 ⁄ 2	5	5 + 1 ⁄ 2	6	6 + 1 ⁄ 2	7	7 + 1 ⁄ 2	8	8 + 1 ⁄ 2	9	9 + 1 ⁄ 2	10	10 + 1 ⁄ 2	11	11 + 1 ⁄ 2	12	12 + 1 ⁄ 2	13	13 + 1 ⁄ 2	14
Н	0.7	0.8	1.0	1.2	1.4	1.7	2	2.4	2.8	3.3	4	4.8	5.6	6.7	8	9.5	11	13	16	19	22	27	32	38	45	54	64	76	90	107	128

Типичная шкала диафрагменного числа в

ИЗ	−1	− 2 ⁄ 3	− 1 ⁄ 3	0	1 ⁄ 3	2 ⁄ 3	1	1 + 1 ⁄ 3	1 + 2 ⁄ 3	2	2 + 1 ⁄ 3	2 + 2 ⁄ 3	3	3 + 1 ⁄ 3	3 + 2 ⁄ 3	4	4 + 1 ⁄ 3	4 + 2 ⁄ 3	5	5 + 1 ⁄ 3	5 + 2 ⁄ 3	6	6 + 1 ⁄ 3	6 + 2 ⁄ 3	7	7 + 1 ⁄ 3	7 + 2 ⁄ 3	8	8 + 1 ⁄ 3	8 + 2 ⁄ 3	9	9 + 1 ⁄ 3	9 + 2 ⁄ 3	10	10 + 1 ⁄ 3	10 + 2 ⁄ 3	11	11 + 1 ⁄ 3	11 + 2 ⁄ 3	12	12 + 1 ⁄ 3	12 + 2 ⁄ 3	13
Н	0.7	0.8	0.9	1.0	1.1	1.2	1.4	1.6	1.8	2	2.2	2.5	2.8	3.2	3.5	4	4.5	5.0	5.6	6.3	7.1	8	9	10	11	13	14	16	18	20	22	25	29	32	36	40	45	51	57	64	72	80	90

Иногда одно и то же число включается в несколько шкал; например, апертура f / 1.2 можно использовать как на полустопе, так и на полустопе. или система одной трети стопа; иногда f / 1,3 и f / 3.2 и другие различия используются для шкалы ступени в одну треть.

шкала числа f с шагом в одну

ИЗ	0	1 ⁄ 4	1 ⁄ 2	3 ⁄ 4	1	1 + 1 ⁄ 4	1 + 1 ⁄ 2	1 + 3 ⁄ 4	2	2 + 1 ⁄ 4	2 + 1 ⁄ 2	2 + 3 ⁄ 4	3	3 + 1 ⁄ 4	3 + 1 ⁄ 2	3 + 3 ⁄ 4	4	4 + 1 ⁄ 4	4 + 1 ⁄ 2	4 + 3 ⁄ 4	5
Н	1.0	1.1	1.2	1.3	1.4	1.5	1.7	1.8	2	2.2	2.4	2.6	2.8	3.1	3.3	3.7	4	4.4	4.8	5.2	5.6

ИЗ	5	5 + 1 ⁄ 4	5 + 1 ⁄ 2	5 + 3 ⁄ 4	6	6 + 1 ⁄ 4	6 + 1 ⁄ 2	6 + 3 ⁄ 4	7	7 + 1 ⁄ 4	7 + 1 ⁄ 2	7 + 3 ⁄ 4	8	8 + 1 ⁄ 4	8 + 1 ⁄ 2	8 + 3 ⁄ 4	9	9 + 1 ⁄ 4	9 + 1 ⁄ 2	9 + 3 ⁄ 4	10
Н	5.6	6.2	6.7	7.3	8	8.7	9.5	10	11	12	14	15	16	17	19	21	22	25	27	29	32

H-стоп

H -stop (отверстие, по соглашению пишется заглавной буквой H) — это эквивалент числа f для эффективной экспозиции, основанной на площади, покрытой отверстиями в диффузионных дисках или ситовой апертуре линз Rodenstock Imagon .

Т-стоп

Т -стоп (для остановки передачи, по соглашению пишется заглавной буквой Т) — это число f, скорректированное с учетом эффективности светопропускания ( коэффициента пропускания ). Объектив с Т-ступенью N что и идеальный объектив со 100% пропусканием и числом f N. проецирует изображение той же яркости , конкретной линзы Т-ступень T определяется путем деления числа f на квадратный корень из коэффициента пропускания этой линзы:

$$T={\frac {N}{\sqrt {\text{transmittance}}}}.$$

Например, Объектив f / 2.0 с коэффициентом пропускания 75% имеет Т-стоп 2,3:

$$T={\frac {2.0}{\sqrt {0.75}}}=2.309...$$

Поскольку настоящие линзы имеют коэффициент пропускания менее 100%, число Т-остановки объектива всегда больше, чем его число f.

При потере 8% на поверхность воздух-стекло на линзах без покрытия многослойное покрытие линз является ключевым моментом в конструкции линз для уменьшения потерь пропускания линз. В некоторых обзорах объективов измеряется T-stop или скорость передачи данных в своих тестах. Иногда вместо чисел f используются Т-ступени для более точного определения экспозиции, особенно при использовании внешних экспонометров . Типичный коэффициент пропускания линз составляет 60–95%. Т-образные стопы часто используются в кинематографии, где многие изображения видны в быстрой последовательности, и даже небольшие изменения экспозиции будут заметны. Объективы кинокамер обычно калибруются по Т-ступеням, а не по числам f. В фотосъемке, где нет необходимости строго согласовывать все используемые объективы и камеры, небольшие различия в экспозиции менее важны; однако Т-образные ограничители до сих пор используются в некоторых объективах специального назначения, таких как объективы Smooth Trans Focus от Minolta и Sony .

Номера ASA/ISO

фотопленки Чувствительность сенсора и электронной камеры к свету часто указывается с использованием чисел ASA/ISO . Обе системы имеют линейное число, где удвоение чувствительности обозначается удвоением числа, и логарифмическое число. В системе ISO увеличение логарифмического числа на 3° соответствует удвоению чувствительности. Удвоение или уменьшение чувствительности вдвое равно разнице в коэффициенте пропускания света на один Т-ступень.

Выигрыш

Соотношение диафрагмы и усиления на видеокамерах Panasonic, как описано в руководстве по эксплуатации HC-V785.

Большинство электронных камер позволяют усиливать сигнал, поступающий с приемного элемента. Это усиление обычно называется усилением и измеряется в децибелах. Каждые 6 дБ усиления эквивалентны одному Т-ступеню с точки зрения светопропускания. Многие видеокамеры имеют единый контроль над числом f и коэффициентом усиления объектива. В этом случае, начиная с нулевого усиления и полностью открытой диафрагмы, можно либо увеличить число f, уменьшив размер диафрагмы, пока усиление остается нулевым, либо можно увеличить усиление, пока диафрагма остается полностью открытой.

Правило Санни 16

Примером использования чисел f в фотографии является правило солнечных 16 : примерно правильная экспозиция будет получена в солнечный день, если использовать диафрагму f / 16 и выдержка, близкая к обратной чувствительности ISO пленки; например, при использовании пленки ISO 200, диафрагмы f / 16 и выдержка 1/200 ​ секунды . Затем число f можно отрегулировать в сторону уменьшения для ситуаций с более слабым освещением. Выбор меньшего числа f «открывает» объектив. Выбор большего числа f означает «закрытие» или «остановку» объектива.

Влияние на резкость изображения

Сравнение f / 32 (верхняя левая половина) и f / 5 (правая нижняя половина)

Неглубокий фокус с широко открытой линзой

Глубина резкости увеличивается с увеличением числа f, как показано на изображении здесь. Это означает, что на фотографиях, сделанных с низким числом f (большой диафрагмой), объекты, находящиеся на одном расстоянии, будут в фокусе, а остальная часть изображения (более близкие и дальние элементы) окажется вне фокуса. Это часто используется для фотографий природы и портретов , поскольку размытие фона (эстетическое качество, известное как « боке ») может быть эстетически приятным и фокусировать внимание зрителя на главном объекте на переднем плане. Глубина резкости изображения, полученного с заданным числом f, также зависит от других параметров, включая фокусное расстояние , расстояние до объекта и формат пленки или датчика, используемого для захвата изображения. Глубину резкости можно описать как зависящую только от угла зрения, расстояния до объекта и диаметра входного зрачка (как в методе фон Рора ). В результате форматы меньшего размера будут иметь более глубокое поле зрения, чем форматы большего размера, при том же числе f, на том же расстоянии фокусировки и том же угле обзора, поскольку для создания того же угла меньший формат требует более короткого фокусного расстояния (более широкоугольный объектив). обзора, а глубина резкости увеличивается при более коротких фокусных расстояниях. Следовательно, эффекты уменьшенной глубины резкости потребуют меньших чисел f (и, следовательно, потенциально более сложной или сложной оптики) при использовании камер малого формата, чем при использовании камер большего формата.

Помимо фокусировки, резкость изображения связана с числом f посредством двух различных оптических эффектов: аберрации , возникающей из-за несовершенной конструкции линзы, и дифракции , обусловленной волновой природой света. Оптимальная диафрагма для размытия зависит от конструкции объектива. Для современных стандартных объективов, имеющих 6 или 7 элементов, наиболее резкое изображение часто получается около ж / 5,6– f / 8, тогда как у старых стандартных объективов, имеющих всего 4 элемента ( формула Тессара ), останавливающихся до f / 11 даст максимально резкое изображение. Большее количество элементов в современных объективах позволяет разработчикам компенсировать аберрации, позволяя объективу давать более качественные снимки при меньшем числе f. При малых значениях диафрагмы глубина резкости и аберрации улучшаются, но дифракция приводит к большему распространению света, вызывая размытие.

Освещение также чувствительно к диафрагме. Многие широкоугольные объективы демонстрируют значительное ослабление света ( виньетирование ) по краям при большой диафрагме.

У фотожурналистов есть поговорка: « f / 8 и быть там », а это означает, что быть на сцене важнее, чем беспокоиться о технических деталях. Практически, f / 8 (в форматах 35 мм и больше) обеспечивает достаточную глубину резкости и достаточную светосилу объектива для получения приличной базовой экспозиции в большинстве ситуаций при дневном освещении.

Человеческий глаз

Вычисление числа f человеческого глаза включает в себя вычисление физической апертуры и фокусного расстояния глаза. Ширина зрачка может достигать 6–7 мм, что соответствует максимальной физической апертуре.

Число f человеческого глаза варьируется примерно от f / 8.3 в очень ярко освещенном месте примерно до f / 2.1 в темноте. Для расчета фокусного расстояния необходимо учитывать светопреломляющие свойства жидкостей в глазу. Если относиться к глазу как к обычной камере и объективу, наполненным воздухом, это приводит к неправильному фокусному расстоянию и числу f.

Фокусное соотношение в телескопах

Схема фокусного расстояния простой оптической системы, где $f$ это фокусное расстояние и $D$ диаметр объектива

В астрономии f-число обычно называют фокусным отношением (или f-отношением ), обозначаемым как $N$. Оно по-прежнему определяется как фокусное расстояние $f$ объектива , разделенного на его диаметр $D$ или по диаметру диафрагмы в системе:

$$N={\frac {f}{D}}\quad {\xrightarrow {\times D}}\quad f=ND$$

Несмотря на то, что принципы фокусного соотношения всегда одни и те же, применение этого принципа может различаться. В фотографии фокусное соотношение изменяет освещенность фокальной плоскости (или оптическую мощность на единицу площади изображения) и используется для управления такими переменными, как глубина резкости . При использовании оптического телескопа в астрономии не возникает проблем с глубиной резкости, а яркость звездных точечных источников, выраженная в терминах общей оптической мощности (не разделенной на площадь), является функцией только площади абсолютной апертуры, независимо от фокусного расстояния. Фокусное расстояние определяет поле зрения инструмента и масштаб изображения, которое представляется в фокальной плоскости окуляру , пленочной пластинке или ПЗС-матрице .

Например, 4-метровый телескоп SOAR имеет небольшое поле зрения (около f /16 ), что полезно для изучения звезд. Телескоп LSST диаметром 8,4 м, который будет охватывать все небо каждые три дня, имеет очень большое поле зрения. Его короткое фокусное расстояние 10,3 м ( f /1.2 ) стало возможным благодаря системе коррекции ошибок, которая включает в себя вторичное и третичное зеркала, трехэлементную преломляющую систему, активный монтаж и оптику.

Уравнение камеры (G#)

Уравнение камеры, или G#, представляет собой отношение излучения, достигающего датчика камеры, к излучению в фокальной плоскости объектива камеры :

$$G\#={\frac {1+4N^{2}}{\tau \pi }}\,,$$

где τ — коэффициент пропускания линзы, единицы измерения — обратные стерадианы (ср ⁻¹ ).

Рабочее число f

Число f точно описывает способность объектива собирать свет только для объектов, находящихся на бесконечном расстоянии. Это ограничение обычно игнорируется в фотографии, где число f часто используется независимо от расстояния до объекта. В оптической конструкции часто требуется альтернатива для систем, в которых объект находится недалеко от объектива. В этих случаях рабочее число f используется . Рабочее f-число N _w определяется как:

$$N_{w}\approx {1 \over 2\mathrm {NA} _{i}}\approx \left(1+{\frac {|m|}{P}}\right)N\,,$$

где N — нескорректированное число f, NA _i в пространстве изображения , — числовая апертура объектива $|m|$ — абсолютное значение линзы увеличения для объекта, находящегося на определенном расстоянии, а P — увеличение зрачка . Поскольку увеличение зрачка редко известно, его часто принимают равным 1, что является правильным значением для всех симметричных линз.

В фотографии это означает, что по мере приближения фокуса эффективная диафрагма объектива становится меньше, что делает экспозицию темнее. Рабочее число f в фотографии часто описывается как число f, скорректированное на удлинение объектива с помощью коэффициента сильфона . Это имеет особое значение в макросъемке .

История

Система чисел f для определения относительного отверстия возникла в конце девятнадцатого века, конкурируя с несколькими другими системами обозначения апертуры.

Происхождение

В 1867 году Саттон и Доусон определили «апертурное соотношение», по сути, как обратную величину современного f-числа. В следующей цитате «апертное отношение» равно « 1 ⁄ 24 дюйма рассчитывается как отношение 6 дюймов (150 мм) к 1 ⁄ дюйма (6,4 мм), что соответствует f /24 диафрагма:

В каждом объективе имеется, соответствующее данному апертуру (т. е. отношению диаметра диафрагмы к фокусному расстоянию), определенное расстояние ближнего предмета от него, между которым и бесконечностью все предметы находятся в одинаково хорошем положении. фокус. Например, в однофокальной линзе с фокусом 6 дюймов и 1/4 При стопа (апертурное отношение одна двадцать четвертая) все объекты, расположенные на расстоянии от 20 футов от объектива до бесконечного расстояния от него (например, неподвижная звезда), находятся в одинаково хорошей фокусировке. Поэтому при использовании этого ограничителя двадцать футов называются «диапазоном фокусировки» объектива. Следовательно, диапазон фокусных расстояний — это расстояние до ближайшего объекта, который будет хорошо сфокусирован, когда матовое стекло настроено на очень удаленный объект. В одном и том же объективе диапазон фокусных расстояний будет зависеть от размера используемой диафрагмы, тогда как в разных объективах с одинаковым светосилой диапазон фокусных расстояний будет больше по мере увеличения фокусного расстояния объектива. Термины «апертивное отношение» и «фокусный диапазон» не вошли в общее употребление, но очень желательно, чтобы они вошли во избежание двусмысленности и многословия при рассмотрении свойств фотообъективов.

В 1874 году Джон Генри Даллмейер назвал соотношение $1/N$ «коэффициент интенсивности» линзы:

Светосила . линзы зависит от отношения апертуры к эквивалентному фокусу Чтобы убедиться в этом, разделите эквивалентный фокус на диаметр фактической рабочей апертуры рассматриваемого объектива; и запишите частное как знаменатель с 1 или единицей в числителе. Таким образом, чтобы найти соотношение линзы диаметром 2 дюйма и фокуса 6 дюймов, разделите фокус на диафрагму, или 6, разделенное на 2, будет равно 3; то есть, 1/3 – коэффициент интенсивности.

Хотя у него еще не было доступа к Эрнста Аббе , теории остановок и зрачков который был широко доступен Зигфриду Чапскому в 1893 году. Даллмейер знал, что его рабочая апертура не совпадает с физическим диаметром диафрагмы:

Однако следует отметить, что для нахождения реального отношения интенсивностей необходимо определить диаметр фактического рабочего отверстия. Это легко осуществить в случае одиночных линз или в случае двойных комбинированных линз, используемых с полным отверстием, для чего требуется просто применение циркуля или линейки; но когда используются двойные или тройные комбинированные линзы с упорами, вставленными между комбинациями, это несколько более хлопотно; ибо очевидно, что в этом случае диаметр используемого упора не является мерой фактического пучка света, передаваемого передней комбинацией. Чтобы убедиться в этом, сфокусируйтесь на удаленном предмете, снимите фокусировочный экран и замените его коллодиевым предметным стеклом, предварительно вставив на место приготовленной пластинки кусок картона. Проделайте дыроколом небольшое круглое отверстие в центре картона и теперь уберите в затемненную комнату; поднесите свечу близко к отверстию и наблюдайте за светящимся пятном, видимым на передней комбинации; диаметр этого круга, тщательно измеренный, представляет собой фактическую рабочую апертуру рассматриваемой линзы для конкретного используемого диафрагмы.

Этот момент еще раз подчеркнул Чапский в 1893 году. Согласно английской рецензии на его книгу в 1894 году, «настойчиво настаивают на необходимости четкого различия между эффективной апертурой и диаметром физического упора».

Сын Дж. Х. Даллмейера, Томас Рудольф Даллмейер , изобретатель телеобъектива, в 1899 году придерживался терминологии отношения яркости .

Системы нумерации апертур

Kodak 1922 года выпуска с диафрагмой, отмеченной американскими стопами. Таблица преобразования чисел f была добавлена ​​пользователем.

В то же время существовал ряд систем нумерации диафрагм, разработанных с целью заставить время экспозиции изменяться в прямой или обратной зависимости от диафрагмы, а не от квадрата диафрагменного числа или обратного квадрата апертального отношения или интенсивности. соотношение. Но все эти системы включали некоторую произвольную константу, а не простое соотношение фокусного расстояния и диаметра.

Например, Единая система апертур (США) была принята Фотографическим обществом Великобритании в качестве стандарта в 1880-х годах. Ботамли в 1891 году сказал: «Остановки всех лучших производителей теперь организованы в соответствии с этой системой». US 16 имеет такую ​​же светосилу, как и f / 16, но диафрагмы, которые больше или меньше на точку, используют удвоение или уменьшение числа США вдвое, например f / 11 — это США 8 и f / 8 – это US 4. Требуемое время выдержки прямо пропорционально числу US. Eastman Kodak использовала американские диафрагмы на многих своих камерах, по крайней мере, в 1920-х годах.

К 1895 году Ходжес опровергает Ботамли, говоря, что система чисел f взяла верх: «Это называется f / x , и диафрагмы всех современных объективов хорошей конструкции имеют такую ​​маркировку».

Вот ситуация в 1899 году:

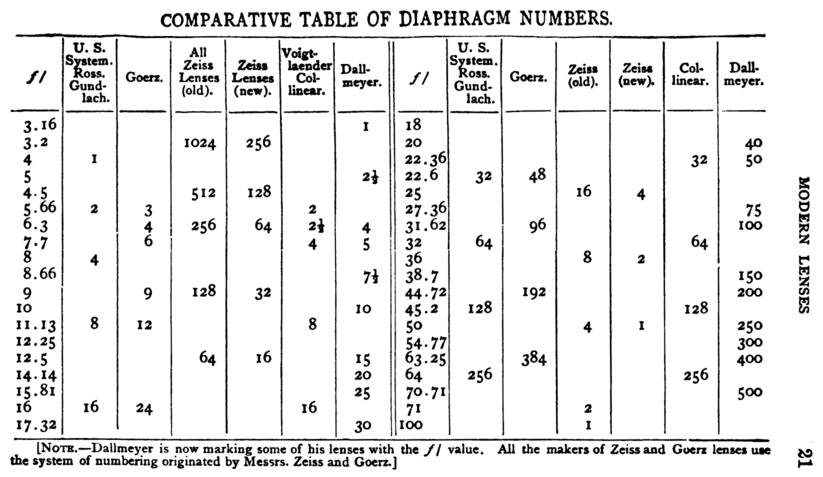
Пайпер в 1901 году обсуждаются пять различных систем маркировки апертуры: старая и новая системы Zeiss, основанные на фактической интенсивности (пропорциональной обратному квадрату числа f); и системы США, CI и Даллмейера, основанные на экспозиции (пропорциональной квадрату числа f). Он называет число f «числом передаточного числа», «числом светосилы» и «отношением диафрагмы». Он называет такие выражения, как f / 8 — «дробный диаметр» апертуры, хотя буквально он равен «абсолютному диаметру», который он выделяет как другой термин. Он также иногда использует такие выражения, как «диафрагма f 8» без деления, обозначенного косой чертой.

Бек и Эндрюс в 1902 году рассказывают о стандарте Королевского фотографического общества. f / 4, f / 5,6, f / 8, f / 11.3 и т. д. RPS изменила свое название и вышла из системы США где-то между 1895 и 1902 годами.

Типографская стандартизация

Камера Yashica-D TLR, вид спереди. Это одна из немногих камер, на которой действительно написано «F-НОМЕР».

В окне настройки диафрагмы Yashica-D сверху используется обозначение «f:». Диафрагма плавно регулируется, без «остановок».

К 1920 году термин f-число появился в книгах как число F, так и f/число . В современных публикациях более распространены формы f-числа и f-числа , хотя более ранние формы, а также F-число все еще встречаются в некоторых книгах; нередко начальная строчная буква f в f-числе или f/number задается курсивом в форме крючка: ƒ.

Обозначения f-числов также были весьма разнообразными в начале двадцатого века. Иногда их писали с большой буквы. иногда с точкой (точкой) вместо косой черты, и иногда устанавливается как вертикальная дробь.

1961 года В стандарте ASA PH2.12-1961 Американского стандарта фотографических экспонометров общего назначения (фотоэлектрического типа) указано, что «символ относительной апертуры должен быть ƒ/ или ƒ: за которым следует эффективное число ƒ». Они показывают изогнутый курсив «ƒ» не только в символе, но и в термине f-числа , который сегодня чаще используется в обычном некурсивном начертании.

См. также

• Круг замешательства
• Группа f/64
• Дизайн фотографического объектива
• Камера-обскура
• Предпочтительный номер

Внешние ссылки

• Широкоформатная фотография: как выбрать диафрагму