Планарная алгебра

В математике планарные алгебры в работе Воана Джонса о стандартном инварианте субфактора II ₁ впервые появились . Они также обеспечивают подходящую алгебраическую основу для многих инвариантов узлов (в частности, полинома Джонса ) и использовались при описании свойств гомологии Хованова относительно композиции клубка . Любая подфакторная планарная алгебра обеспечивает семейство унитарных представлений групп Томпсона . Любую конечную группу (и квантовое обобщение) можно закодировать как плоскую алгебру.

Определение

Идея планарной алгебры состоит в том, чтобы быть диаграмматической аксиоматизацией стандартного инварианта .

Плоский клубок

(Заштрихованный) плоский клубок — это данные конечного числа входных дисков, одного выходного диска, непересекающихся строк, дающих четное число, скажем $2n$, интервалы на диск и один $\star$- отмеченный интервал на диск.

Здесь знак отображается в виде $\star$-форма. На каждом входном диске он размещается между двумя соседними исходящими строками, а на выходном диске — между двумя соседними входящими строками. Плоский клубок определен с точностью до изотопии .

Состав

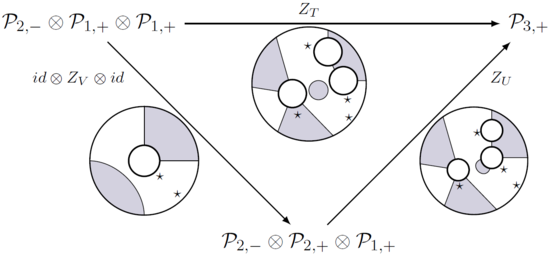
Чтобы составить два плоских клубка, поместите выходной диск одного во вход другого, имея столько интервалов, одинаковую штриховку отмеченных интервалов и так, чтобы $\star$-отмеченные интервалы совпадают. Наконец убираем совпадающие круги. Обратите внимание, что два плоских клубка могут иметь ноль, одну или несколько возможных композиций.

Управляемый планарный

Плоская операда — это множество всех плоских клубков (с точностью до изоморфизма) с такими композициями.

Планарная алгебра

Плоская алгебра — это представление планарной операды; точнее, это семейство векторных пространств $({\mathcal {P}}_{n,\pm })_{n\in \mathbb {N} }$, называется $n$-коробочные пространства, на которых действует плоская операда, т.е. для любой клубки $T$ (с одним выходным диском и $r$ входные диски с $2n_{0}$ и $2n_{1},\dots ,2n_{r}$ интервалы соответственно) существует полилинейное отображение

$Z_{T}:{\mathcal {P}}_{n_{1},\epsilon _{1}}\otimes \cdots \otimes {\mathcal {P}}_{n_{r},\epsilon _{r}}\to {\mathcal {P}}_{n_{0},\epsilon _{0}}$

с $\epsilon _{i}\in \{+,-\}$ в соответствии с затенением $\star$-отмеченные интервалы, и эти карты (также называемые статистическими суммами) учитывают состав клубка таким образом, что все приведенные ниже диаграммы коммутируют.

Примеры

Плоские клубки

Семейство векторных пространств $({\mathcal {T}}_{n,\pm })_{n\in \mathbb {N} }$ генерируются плоскими клубками, имеющими $2n$ интервалы на их выходном диске и белый (или черный) $\star$-отмеченный интервал допускает структуру планарной алгебры.

Темперли-Либ

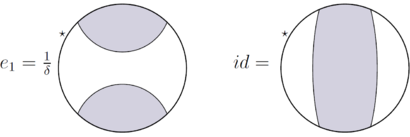
Плоская алгебра Темперли-Либа ${\mathcal {TL}}(\delta )$ генерируется плоскими клубками без входного диска; его $3$-коробочное пространство ${\mathcal {TL}}_{3,+}(\delta )$ генерируется

Более того, замкнутая строка заменяется умножением на $\delta$.

Обратите внимание, что размерность ${\mathcal {TL}}_{n,\pm }(\delta )$ это каталонский номер ${\frac {1}{n+1}}{\binom {2n}{n}}$.Эта плоская алгебра кодирует понятие алгебры Темперли – Либа .

алгебра Хопфа

Полупростая и кополупростая алгебра Хопфа над алгебраически замкнутым полем кодируется в планарной алгебре, определяемой образующими и соотношениями, и «соответствует» (с точностью до изоморфизма) связной, неприводимой, сферической, невырожденной планарной алгебре с ненулевым модулем. $\delta$ и глубины два.

Обратите внимание, что подключено означает $\dim({\mathcal {P}}_{0,\pm })=1$ (как и в случае оценки ниже), неприводимые средства $\dim({\mathcal {P}}_{1,+})=1$, сферический определяется ниже, а невырожденный означает, что трассы (определенные ниже) невырождены.

Субфактор планарной алгебры

Определение

Субфактор планарной алгебры — это планарная $\star$-алгебра $({\mathcal {P}}_{n,\pm })_{n\in \mathbb {N} }$ что такое:

(1) Конечномерные: $\dim({\mathcal {P}}_{n,\pm })<\infty$

(2) Оцениваемый: ${\mathcal {P}}_{0,\pm }=\mathbb {C}$

(3) Сферический: $tr:=tr_{r}=tr_{l}$

(4) Положительный: $\langle a\vert b\rangle =tr(b^{\star }a)$ определяет внутренний продукт.

Обратите внимание, что согласно (2) и (3), любая замкнутая строка (заштрихованная или нет) считается одной и той же константой. $\delta$.

Действие «запутывание» взаимодействует с сопряженным посредством:

$Z_{T}(a_{1}\otimes a_{2}\otimes \cdots \otimes a_{r})^{\star }=Z_{T^{\star }}(a_{1}^{\star }\otimes a_{2}^{\star }\otimes \cdots \otimes a_{r}^{\star })$

с $T^{\star }$ зеркальное отражение $T$ и $a_{i}^{\star }$ сопряжение $a_{i}$ в ${\mathcal {P}}_{n_{i},\epsilon _{i}}$.

Примеры и результаты

Теорема об отсутствии призраков : плоская алгебра ${\mathcal {TL}}(\delta )$ не имеет призрака (т.е. элемента $a$ с $\langle a\vert a\rangle <0$) тогда и только тогда, когда

$\delta \in \{2\cos(\pi /n)|n=3,4,5,...\}\cup [2,+\infty ]$

Для $\delta$ как указано выше, пусть ${\mathcal {I}}$ быть нулевым идеалом (порожденным элементами $a$ с $\langle a\vert a\rangle =0$). Тогда частное ${\mathcal {TL}}(\delta )/{\mathcal {I}}$ является субфакторной планарной алгеброй, называемой субфакторной планарной алгеброй Темперли – Либа-Джонса. ${\mathcal {TLJ}}(\delta )$. Любая подфакторная планарная алгебра с константой $\delta$ признает ${\mathcal {TLJ}}(\delta )$ как плоская подалгебра.

Плоская алгебра $({\mathcal {P}}_{n,\pm })$ является субфакторной планарной алгеброй тогда и только тогда, когда она является стандартным инвариантом экстремального субфактора $N\subseteq M$ индекса $[M:N]=\delta ^{2}$, с ${\mathcal {P}}_{n,+}=N'\cap M_{n-1}$ и ${\mathcal {P}}_{n,-}=M'\cap M_{n}$. Конечная глубина или неприводимый подфактор экстремальны ( $tr_{N'}=tr_{M}$ на $N'\cap M$).

Существует подфакторная плоская алгебра, кодирующая любую конечную группу (и, в более общем плане, любую конечномерную группу Хопфа) . ${\rm {C}}^{\star }$-алгебра , называемая алгеброй Каца), определяемая генераторами и отношениями. (Конечномерная) алгебра Каца «соответствует» (с точностью до изоморфизма) неприводимой подфакторной планарной алгебре глубины два.

Субфактор планарная алгебра, ассоциированная с включением конечных групп, не всегда запоминает (безсердечниковое) включение.

Планарная алгебра субфакторов Биша-Джонса ${\mathcal {BJ}}(\delta _{1},\delta _{2})$ (иногда называемый Фусс-каталонским) определяется как ${\mathcal {TLJ}}(\delta )$ но разрешив два цвета строки с собственной константой $\delta _{1}$ и $\delta _{2}$, с $\delta _{i}$ как указано выше. Это плоская подалгебра любой подфакторной планарной алгебры с промежуточным, такая что $[K:N]=\delta _{1}^{2}$ и $[M:K]=\delta _{2}^{2}$.

Первая планарная алгебра субфактора конечной глубины индекса $\delta ^{2}>4$ называется планарной алгеброй субфактора Хаагерупа . Он имеет индекс $(5+{\sqrt {13}})/2\sim 4.303$.

Планарные алгебры субфакторов полностью классифицированы по индексу не более $5$и немного дальше. Эта классификация была инициирована Уффе Хаагерупом . Он использует (среди прочего) список возможных основных графов вместе с теоремой вложения. и алгоритм медузы.

Планарная алгебра субфакторов запоминает субфактор (т. е. ее стандартный инвариант является полным), если он аменабельен. Подфактор гиперконечной конечной глубины возможен.

О неподдающемся случаю: существует неклассифицируемое множество неприводимых гиперконечных подфакторов индекса 6, которые имеют один и тот же стандартный инвариант.

Преобразование Фурье и бипроекции

Позволять $N\subset M$ быть подфактором конечного индекса, и ${\mathcal {P}}$ соответствующий подфактор планарной алгебры. Предположим, что ${\mathcal {P}}$ является неприводимым (т.е. ${\mathcal {P}}_{1,+}=N'\cap M_{1}=\mathbb {C}$). Позволять $N\subset K\subset M$ быть промежуточным субфактором. Пусть проекция Джонса $e_{K}^{M}:L^{2}(M)\to L^{2}(K)$. Обратите внимание, что $e_{K}^{M}\in {\mathcal {P}}_{2,+}$. Позволять $id:=e_{M}^{M}$ и $e_{1}:=e_{N}^{M}$.

Обратите внимание, что $tr(e_{1})=\delta ^{-2}=[M:N]^{-1}$ и $tr(id)=1$.

Пусть биективное линейное отображение ${\mathcal {F}}:{\mathcal {P}}_{2,\pm }\to {\mathcal {P}}_{2,\mp }$ быть преобразованием Фурье , также называемым $1$-щелкните (внешней звезды) или $90^{\circ }$ вращение; и пусть $a*b$ быть сопродюсером ​ $a$ и $b$.

Обратите внимание, что слово «копродукт» является уменьшительным от слова «продукт свертки» . Это бинарная операция.

Копроизведение удовлетворяет равенству $a*b={\mathcal {F}}({\mathcal {F}}^{-1}(a){\mathcal {F}}^{-1}(b)).$

Для любых положительных операторов $a,b$, попутное произведение $a*b$ также является положительным; это можно увидеть схематически:

Позволять ${\overline {a}}:={\mathcal {F}}({\mathcal {F}}(a))$ быть контрагредиентом $a$ (также называемый $180^{\circ }$ вращение). Карта ${\mathcal {F}}^{4}$ соответствует четырем $1$-щелчки внешней звезды, так что это идентификационная карта, а затем ${\overline {\overline {a}}}=a$.

В случае алгебры Каца контрагредиент является в точности антиподом: что для конечной группы соответствует обратному.

Бипроекция – это проекция $b\in {\mathcal {P}}_{2,+}\setminus \{0\}$ с ${\mathcal {F}}(b)$ кратное проекции. Обратите внимание, что $e_{1}=e_{N}^{M}$ и $id=e_{M}^{M}$ являются бипроекциями; это можно увидеть следующим образом:

Проекция $b$ является бипроекцией тогда и только тогда, когда это проекция Джонса $e_{K}^{M}$ промежуточного субфактора $N\subset K\subset M$, если только $e_{1}\leq b={\overline {b}}=\lambda b*b,{\text{ with }}\lambda ^{-1}=\delta tr(b)$.

Переписка Галуа : в случае алгебры Каца бипроекции имеют номер 1–1 с левыми коидеальными подалгебрами, которые для конечной группы соответствуют подгруппам.

Для любой неприводимой подфакторной планарной алгебры множество бипроекций представляет собой конечную решетку: формы $[e_{1},id]$, как для интервала конечных групп $[H,G]$.

Используя бипроекции, мы можем сделать промежуточные подфакторы планарными алгебрами.

Принцип неопределенности распространяется на любую неприводимую плоскую алгебру подфакторов. ${\mathcal {P}}$:

Позволять ${\mathcal {S}}(x)=Tr(R(x))$ с $R(x)$ проекция дальности $x$ и $Tr$ ненормированный след (т.е. $Tr=\delta ^{n}tr$ на ${\mathcal {P}}_{n,\pm }$).

Некоммутативный принцип неопределенности : Позволять $x\in {\mathcal {P}}_{2,\pm }$, ненулевой. Затем

${\mathcal {S}}(x){\mathcal {S}}({\mathcal {F}}(x))\geq \delta ^{2}$

Предполагая $x$ и ${\mathcal {F}}(x)$ положительно, равенство имеет место тогда и только тогда, когда $x$ является бипроекцией. В более общем смысле равенство имеет место тогда и только тогда, когда $x$ - это би-сдвиг бипроекции.