Самолет Бенц

В математике плоскость Бенца — это тип двумерной геометрической структуры , названной в честь немецкого математика Вальтера Бенца . Термин применялся к группе объектов, возникающих в результате общей аксиоматизации определенных структур и распадающихся на три семейства, которые вводились отдельно: плоскости Мёбиуса , плоскости Лагерра и плоскости Минковского . ^[1]^[2]

Möbius plane Мёбиуса editСамолет

Классический самолет Мёбиуса: 2d/3d модель

Начиная с реальной евклидовой плоскости и объединяя набор линий с набором окружностей для формирования набора блоков, мы получаем неоднородную структуру инцидентности : три отдельные точки определяют один блок, но линии различимы как набор блоков, которые попарно пересекаются друг с другом. в одной точке без касания (или без точек, когда они параллельны). Добавление к точке устанавливает новую точку $\infty$ , определенный так, чтобы лежать на каждой линии, приводит к тому, что каждый блок определяется ровно тремя точками, а также пересечение любых двух блоков по единообразному шаблону (пересекающееся в двух точках, касательное или непересекающееся). Эта однородная геометрия называется классической инверсной геометрией или плоскостью Мёбиуса. Неоднородность описания (линии, круги, новая точка) можно считать несущественной, если использовать трехмерную модель. Используя стереографическую проекцию , можно увидеть, что классическая плоскость Мёбиуса изоморфна геометрии плоских сечений (окружностей) на сфере в евклидовом 3-пространстве.

Аналогично (аксиоматической) проективной плоскости (аксиоматическая) плоскость Мёбиуса определяет структуру инцидентности. Плоскости Мёбиуса аналогичным образом могут быть построены над полями, отличными от действительных чисел.

Лагер editзависает

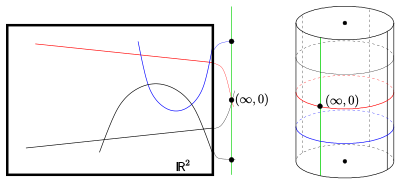
Классический самолет Лагерра: 2d/3d-модель

Начиная снова с $\textstyle \mathbb {R} ^{2}$ и взяв кривые с помощью уравнений $y=ax^{2}+bx+c$ (параболы и линии) в виде блоков эффективна следующая гомогенизация: Добавить к кривой $y=ax^{2}+bx+c$ новая точка $(\infty ,a)$ . Следовательно, набор точек равен $(\mathbb {R} \cup {\infty })\times \mathbb {R}$ . Такая геометрия парабол называется классической плоскостью Лагерра (первоначально она задумывалась как геометрия ориентированных прямых и окружностей. Обе геометрии изоморфны.)

Что касается плоскости Мёбиуса, то существует трёхмерная модель: геометрия эллиптических плоских сечений на ортогональном цилиндре (в $\mathbb {R} ^{3}$ ). Абстракция приводит (аналогично плоскости Мёбиуса) к аксиоматической плоскости Лагерра.

Самолет Минковского [ править ]

Классический самолет Минковского: 2d/3d-модель

Начиная с $\mathbb {R} ^{2}$ и объединение строк $y=mx+d,m\neq 0$ с гиперболами $y={\tfrac {a}{x-b}}+c,a\neq 0$ Чтобы получить набор блоков, следующая идея гомогенизирует структуру инцидентности: добавьте к любой линии точку $(\infty ,\infty )$ и к любой гиперболе $y={\tfrac {a}{x-b}}+c,a\neq 0$ две точки $(b,\infty ),(\infty ,c)$ . Следовательно, набор точек $(\mathbb {R} \cup \{\infty \})^{2}$ . Такая геометрия гипербол называется классической плоскостью Минковского.

Аналогично классическим плоскостям Мёбиуса и Лагерра существует трёхмерная модель: классическая плоскость Минковского изоморфна геометрии плоских сечений однолистного гиперболоида (невырожденной квадрики индекса 2) в трёхмерном проективном пространстве. . Аналогично первым двум случаям мы получаем (аксиоматическую) плоскость Минковского.

Геометрия плоского круга Бенца плоскости или

Из-за существенной роли круга (рассматриваемого как невырожденная коника на проективной плоскости ) и плоского описания исходных моделей три типа геометрий отнесены к плоским геометриям круга или в честь Вальтера Бенца, который считал их геометрические структуры с общепринятой точки зрения, плоскости Бенца.

См. также [ править ]

Ссылки [ править ]

^ В. Бенц, Лекции по геометрии алгебр , Springer (1973)
^ Ф. Букенхаут (редактор), Справочник по геометрии падения , Elsevier (1995). ISBN 0-444-88355-X

Фрэнсис Бюкенхаут (1981) «Планы Бенца», Journal of Geometry 17 (1): 61–8.

Внешние ссылки [ править ]

Самолет Бенца из Математической энциклопедии
Геометрия плоского круга Эриха Хартмана , введение в плоскости Мебиуса, Лагерра и Минковского, Дармштадтский технологический университет.

[1] В. Бенц, Лекции по геометрии алгебр , Springer (1973)

[2] Ф. Букенхаут (редактор), Справочник по геометрии падения , Elsevier (1995). ISBN 0-444-88355-X

[1]

[2]