Лагер зависает

В математике плоскость Лагерра является одним из трех типов плоскости Бенца : плоскость Мёбиуса , плоскость Лагерра и плоскость Минковского . Плоскости Лагерра названы в честь французского математика Эдмона Николя Лагерра .

Классический самолет Лагерра: 2d/3d-модель

Классическая плоскость Лагерра представляет собой структуру инцидентности , описывающую поведение кривых инцидентности. $y=ax^{2}+bx+c$ , т. е. параболы и прямые в реальной аффинной плоскости . Для упрощения конструкции к любой кривой $y=ax^{2}+bx+c$ суть $(\infty ,a)$ добавляется. Еще одним преимуществом этого завершения является то, что плоская геометрия завершенных парабол/линий изоморфна геометрии плоских сечений цилиндра (см . Ниже).

Классический

Первоначально классическая плоскость Лагерра определялась как геометрия ориентированных прямых и окружностей на действительной евклидовой плоскости (см. ). Здесь мы предпочитаем параболическую модель классической плоскости Лагерра.

Мы определяем:

${\mathcal {P}}:=\mathbb {R} ^{2}\cup (\{\infty \}\times \mathbb {R} ),\ \infty \notin \mathbb {R} ,$ набор точек , ${\mathcal {Z}}:=\{\{(x,y)\in \mathbb {R} ^{2}\mid y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\mid a,b,c\in \mathbb {R} \}$ набор циклов .

Структура заболеваемости $({\mathcal {P}},{\mathcal {Z}},\in )$ называется классической плоскостью Лагерра .

Набор точек $\mathbb {R} ^{2}$ плюс копия $\mathbb {R}$ (см. рисунок). Любая парабола/линия $y=ax^{2}+bx+c$ получает дополнительный балл $(\infty ,a)$.

Точки с одинаковой координатой x не могут быть соединены кривыми. $y=ax^{2}+bx+c$. Следовательно, мы определяем:

Две точки $A,B$ параллельны ​ ( $A\parallel B$)если $A=B$ или нет цикла, содержащего $A$ и $B$.

Для описания классической вещественной плоскости Лагерра над двумя точками $(a_{1},a_{2}),(b_{1},b_{2})$ параллельны тогда и только тогда, когда $a_{1}=b_{1}$. $\parallel$ — отношение эквивалентности , аналогичное параллельности прямых.

Структура заболеваемости $({\mathcal {P}},{\mathcal {Z}},\in )$ имеет следующие свойства:

Лемма:

• За любые три точки $A,B,C$, попарно не параллельно, имеется ровно один цикл $z$ содержащий $A,B,C$.
• Для любой точки $P$ и любой цикл $z$ есть ровно одна точка $P'\in z$ такой, что $P\parallel P'$.
• Для любого цикла $z$, любая точка $P\in z$ и любая точка $Q\notin z$ это не параллельно $P$ существует ровно один цикл $z'$ через $P,Q$ с $z\cap z'=\{P\}$, то есть $z$ и $z'$ касаться друг друга в $P$.

Плоскость Лагерра: стереографическая проекция плоскости xz на цилиндр.

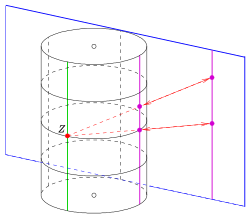
Подобно сферической модели классической плоскости Мебиуса, существует цилиндрическая модель для классической плоскости Лагерра :

$({\mathcal {P}},{\mathcal {Z}},\in )$ изоморфна геометрии плоских сечений кругового цилиндра в $\mathbb {R} ^{3}$ .

Следующее отображение $\Phi$ это проекция с центром $(0,1,0)$ которое отображает плоскость xz на цилиндр с помощью уравнения $u^{2}+v^{2}-v=0$, ось $(0,{\tfrac {1}{2}},..)$ и радиус $r={\tfrac {1}{2}}\ :$

$\Phi :\ (x,z)\rightarrow ({\frac {x}{1+x^{2}}},{\frac {x^{2}}{1+x^{2}}},{\frac {z}{1+x^{2}}})=(u,v,w)\ .$

• Очки $(0,1,a)$ (линия на цилиндре, проходящая через центр) отображаются не как изображения.
• $\Phi$ проецирует параболу/линию с помощью уравнения $z=ax^{2}+bx+c$ в самолет $w-a=bu+(a-c)(v-1)$. Итак, изображение параболы/линии – это плоское сечение цилиндра с неперпендикулярной плоскостью и, следовательно, круг/эллипс без точки. $(0,1,a)$. Параболы/линии $z=ax^{2}+a$ отображаются на (горизонтальные) круги.
• Линия (a=0) отображается на круг/эллипс, проходящий через центр. $(0,1,0)$ и парабола ( $a\neq 0$) на круг/эллипс, не содержащий $(0,1,0)$.

Аксиомы плоскости Лагерра

Приведенная выше лемма приводит к следующему определению:

Позволять ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ быть структурой инцидентности с множеством точек ${\mathcal {P}}$ и набор циклов ${\mathcal {Z}}$.
Две точки $A,B$ параллельны ​ ( $A\parallel B$) если $A=B$ или нет цикла, содержащего $A$ и $B$.
${\mathcal {L}}$ называется плоскостью Лагерра, если выполняются следующие аксиомы:

Плоскость Лагерра: аксиомы

B1: По любым трем пунктам $A,B,C$, попарно не параллельно, имеется ровно один цикл $z$ который содержит $A,B,C$.

B2: Для любой точки $P$ и любой цикл $z$ есть ровно одна точка $P'\in z$ такой, что $P\parallel P'$.

B3: Для любого цикла $z$, любая точка $P\in z$ и любая точка $Q\notin z$ это не параллельно $P$ существует ровно один цикл $z'$ через $P,Q$ с $z\cap z'=\{P\}$,

т.е. $z$ и $z'$ касаться друг друга в $P$.

B4: Любой цикл содержит минимум три точки. Есть как минимум один цикл. Есть как минимум четыре точки, не входящие в цикл.

Четыре очка $A,B,C,D$ являются конциклическими, если существует цикл $z$ с $A,B,C,D\in z$.

Из определения отношения $\parallel$ и аксиому B2 получаем

Лемма: Связь $\parallel$ является отношением эквивалентности .

Следуя цилиндрической модели классической плоскости Лагерра, введем обозначение:

а) Для $P\in {\mathcal {P}}$ мы устанавливаем ${\overline {P}}:=\{Q\in {\mathcal {P}}\ |\ P\parallel Q\}$.б) Класс эквивалентности ${\overline {P}}$ называется генератором .

Для классической плоскости Лагерра образующей является линия, параллельная оси Y (плоская модель) или линия на цилиндре (пространственная модель).

Связь с линейной геометрией дается следующим определением:

Для самолета Лагерра ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ мы определяем локальную структуру

${\mathcal {A}}_{P}:=({\mathcal {P}}\setminus \{{\overline {P}}\},\{z\setminus \{{\overline {P}}\}\ |\ P\in z\in {\mathcal {Z}}\}\cup \{{\overline {Q}}\ |\ Q\in {\mathcal {P}}\setminus \{{\overline {P}}\},\in )$

и назовем его остатком в точке P.

В плоской модели классической плоскости Лагерра ${\mathcal {A}}_{\infty }$ это настоящая аффинная плоскость $\mathbb {R} ^{2}$.В общем, мы получаем

Теорема: Любой вычет плоскости Лагерра является аффинной плоскостью .

И эквивалентное определение плоскости Лагерра:

Теорема: Структура инцидентности вместе с отношением эквивалентности $\parallel$ на ${\mathcal {P}}$ этоПлоскость Лагерра тогда и только тогда, когда для любой точки $P$ остаток ${\mathcal {A}}_{P}$ является аффинной плоскостью.

минимальная модель плоскости Лагерра (показаны только 4 цикла из 8)

Следующая структура инцидентности представляет собой «минимальную модель» плоскости Лагерра:

${\mathcal {P}}:=\{A_{1},A_{2},B_{1},B_{2},C_{1},C_{2}\}\ ,$

${\mathcal {Z}}:=\{\{A_{i},B_{j},C_{k}\}\ |\ i,j,k=1,2\}\ ,$

$A_{1}\parallel A_{2},\ B_{1}\parallel B_{2},\ C_{1}\parallel C_{2}\ .$

Следовательно $|{\mathcal {P}}|=6$ и $|{\mathcal {Z}}|=8\ .$

Для конечных плоскостей Лагерра, т.е. $|{\mathcal {P}}|<\infty$, мы получаем:

Лемма: Для любых циклов $z_{1},z_{2}$ и любой генератор ${\overline {P}}$ конечной Лагерра плоскости ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ у нас есть:

$|z_{1}|=|z_{2}|=|{\overline {P}}|+1$.

Для конечной плоскости Лагерра ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ и цикл $z\in {\mathcal {Z}}$ целое число $n:=|z|-1$ называется порядком ​ ${\mathcal {L}}$.

Из комбинаторики получаем

Лемма: Позволять ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ быть Лагерром — плоскостью порядка $n$. Затем

а) любой остаток ${\mathcal {A}}_{P}$ является аффинной плоскостью порядка $n\quad ,$ б) $|{\mathcal {P}}|=n^{2}+n,$ в) $|{\mathcal {Z}}|=n^{3}.$

Микельяна

В отличие от плоскостей Мебиуса формальное обобщение классической модели плоскости Лагерра, т.е. замена $\mathbb {R}$ по произвольному полю $K$, всегда приводит к примеру плоскости Лагерра.

Теорема: Для поля $K$ и

${\mathcal {P}}:=K^{2}\cup$ $(\{\infty \}\times K),\ \infty \notin K$,

${\mathcal {Z}}:=\{\{(x,y)\in K^{2}\ |\ y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\ |\ a,b,c\in K\}$ структура заболеваемости

${\mathcal {L}}(K):=({\mathcal {P}},{\mathcal {Z}},\in )$ является плоскостью Лагерра со следующим соотношением параллельности: $(a_{1},a_{2})\parallel (b_{1},b_{2})$ тогда и только тогда, когда $a_{1}=b_{1}$.

Аналогично плоскости Мёбиуса справедлива версия Лагерра теоремы Микеля:

Теорема Микеля (вместо парабол нарисованы круги)

Теорема Микеля: Для самолета Лагерра ${\mathcal {L}}(K)$ верно следующее:

Если для любых 8 попарно непараллельных точек $P_{1},\ldots ,P_{8}$ которые можно сопоставить вершинам куба так, что точки в пяти гранях соответствуют конциклическим четверкам, то шестая четверка точек тоже конциклична.

(Для лучшего обзора на рисунке вместо парабол нарисованы круги)

Важность теоремы Микеля проявляется в следующей теореме, принадлежащей В.Д. Вардену, Смиду и Чену:

Теорема: только плоскость Лагерра. ${\mathcal {L}}(K)$ удовлетворяет теореме Микеля.

По последней теореме ${\mathcal {L}}(K)$ называется «микелианской плоскостью Лагерра».

Минимальная модель плоскости Лагерра — микелевская. Он изоморфен плоскости Лагерра. ${\mathcal {L}}(K)$ с $K=GF(2)$ (поле $\{0,1\}$).

Подходящая стереографическая проекция показывает, что ${\mathcal {L}}(K)$ изоморфна геометрии плоских сечений квадратичного цилиндра над полем $K$.

Овоидальные плоскости Лагерра

Есть много самолетов Лагерра, которые не являются микельскими (см. ссылку ниже). Класс, наиболее похожий на микелевские плоскости Лагерра, — это яйцевидные плоскости Лагерра . Овоидальная плоскость Лагерра — это геометрия плоских сечений цилиндра, построенная с использованием овала вместо невырожденной конической. Овал является квадратичным множеством и обладает теми же геометрическими свойствами, что и невырожденная коника на проективной плоскости: 1) прямая пересекает овал в нуле, одной или двух точках и 2) в любой точке существует единственная касательная. Простой овал на реальной плоскости можно построить, склеив две подходящие половинки разных эллипсов так, чтобы в результате не получилась коника. Даже в конечном случае существуют овалы (см. квадратичное множество ).

См. также

• Преобразования Лагерра

Внешние ссылки

• Самолет Бенца в математической энциклопедии
• Конспект лекции «Геометрия плоского круга : введение в плоскости Мебиуса, Лагерра и Минковского», стр. 67