Кейлс
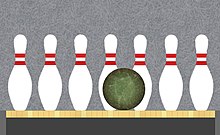
Кейлс — это простая беспристрастная игра в комбинаторной теории игр , изобретенная Генри Дюдени в 1908 году. Учитывая ряд воображаемых кеглей для боулинга, игроки по очереди выбивают одну или две соседние кегли, пока все кегли не исчезнут. Используя обозначение восьмеричных игр , Кейлс обозначается 0,77 .
Правила [ править ]
В Кейлс играют с рядом жетонов, которые представляют собой кегли для боулинга. Длина строки может быть любой. Два игрока чередуются; каждый игрок в свой ход может удалить либо любую одну кеглю (шар, поданный прямо в эту кеглю), либо две соседние кегли (шар, поданный так, чтобы ударить по обеим). Согласно правилам обычной игры , игрок проигрывает, если у него нет правильного хода (то есть, когда все кегли исчезли). В игру также можно играть, используя мизера правила игрок, который не может двигаться ; в этом случае побеждает .
История [ править ]
Кейлс был изобретен Генри Дюдени . [1] [2] Ричард Гай и Седрик Смит были первыми, кто полностью проанализировал версию обычной игры, используя теорию Спрэга-Грунди . [3] [4] Версия misère была проанализирована Уильямом Сибертом в 1973 году, но он опубликовал свою работу только в 1989 году. [5]
Имя «Кейлс» является англизированной формой французского слова quilles , что означает «кегли для боулинга».
Анализ [ править ]
Большинство игроков быстро обнаруживают, что первый игрок имеет гарантированный выигрыш в обычном методе Кейлса, когда длина строки больше нуля. Этого выигрыша можно добиться, используя стратегию симметрии . При первом ходе первый игрок должен сделать ход так, чтобы ряд был разбит на две части одинаковой длины. Это ограничивает все будущие перемещения тем или иным разделом. Теперь первый игрок просто имитирует ходы второго игрока в противоположном ряду.
Гораздо интереснее спросить, каково значение нима для строки длины . Это часто обозначается ; это число , а не число . По Спрэга–Грунди теореме — это результат всех возможных ходов ним-суммы ним -значений двух результирующих секций. Например,
потому что из строки длиной 5 можно перейти на позиции
Рекурсивный расчет значений (начиная с ) дает результаты, обобщенные в следующей таблице. Чтобы найти значение на столе напиши как и посмотрите на строку a, столбец b:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0+ | 0 | 1 | 2 | 3 | 1 | 4 | 3 | 2 | 1 | 4 | 2 | 6 |
| 12+ | 4 | 1 | 2 | 7 | 1 | 4 | 3 | 2 | 1 | 4 | 6 | 7 |
| 24+ | 4 | 1 | 2 | 8 | 5 | 4 | 7 | 2 | 1 | 8 | 6 | 7 |
| 36+ | 4 | 1 | 2 | 3 | 1 | 4 | 7 | 2 | 1 | 8 | 2 | 7 |
| 48+ | 4 | 1 | 2 | 8 | 1 | 4 | 7 | 2 | 1 | 4 | 2 | 7 |
| 60+ | 4 | 1 | 2 | 8 | 1 | 4 | 7 | 2 | 1 | 8 | 6 | 7 |
| 72+ | 4 | 1 | 2 | 8 | 1 | 4 | 7 | 2 | 1 | 8 | 2 | 7 |
В этот момент последовательность значений nim становится периодической. [5] с периодом 12, поэтому все дальнейшие строки таблицы идентичны последней строке.
Приложения [ править ]
Поскольку определенные позиции в точках и прямоугольниках сводятся к позициям Кейлса, [6] полезно понять Кейлса, чтобы проанализировать общее положение точек и прямоугольников.
Вычислительная сложность [ править ]
При обычной игре задачу Кейлса можно решить за полиномиальное время, используя теорию Спрэга-Грунди. [3]
Обобщения [ править ]
Узел Кейлса — это обобщение Кейлса на графы , в которых каждая чаша «сбивает» (удаляет) искомую вершину и все соседние с ней вершины. Альтернативно, эту игру можно рассматривать как два игрока, которые вместе находят независимый набор . Определение победителя решается за полиномиальное время для любого семейства графов с ограниченным астероидным числом (определяемым как размер наибольшего подмножества вершин, такого, что удаление замкнутой окрестности любой вершины в наборе оставляет оставшиеся вершины набора в та же связная компонента). [7]
Аналогично, в игре с формированием клики два игрока должны найти клику в графе. Побеждает тот, кто сыграет последним. Шефер (1978) [8] доказал, что решение исхода этих игр является PSPACE-полным . Тот же результат справедлив и для партийной версии узла Кейлса, в которой для каждого узла только одному из игроков разрешено выбрать этот конкретный узел в качестве цели для сбивания.
См. также [ править ]
Ссылки [ править ]
- ^ Дадени, HE (2002), Кентерберийские загадки , Дувр, стр. 118–119, головоломка 73, ISBN 0-486-42558-4 . Первоначально опубликовано в 1908 году.
- ^ Конвей, Джон Х. О числах и играх. Академик Пресс, 1976.
- ^ Jump up to: Перейти обратно: а б Р.К. Гай и КЭБ Смит, G -значения различных игр, Proc. Кембриджская философия. Соц., 52 (1956) 514–526.
- ^ Т. Э. Пламбек, Дейзи, Кейлс и разложение Сиберта-Конвея в жалких восьмеричных играх. Архивировано 14 июля 2010 г. в Wayback Machine , Theoret. Вычислить. Sci (Математические игры) (1992) 96 361–388.
- ^ Jump up to: Перейти обратно: а б Пламбек, Тейн, Кейлс , заархивировано из оригинала 12 октября 2008 г. , получено 15 августа 2008 г.
- ^ Э. Берлекамп , Дж. Х. Конвей , Р. Гай. Пути выигрыша в математических играх . Академик Пресс, 1982.
- ^ Бодлендер, Ханс Л. (2015). «Точные алгоритмы Кейлса». Теоретическая информатика . 562 : 165–176. дои : 10.1016/j.tcs.2014.09.042 .
- ^ Шефер, Томас Дж. (1978). «О сложности некоторых игр двух лиц с совершенной информацией». Журнал компьютерных и системных наук . 16 (2): 185–225. дои : 10.1016/0022-0000(78)90045-4 .






