Метастабильность (электроника)

В электронике — метастабильность это способность цифровой электронной системы сохраняться в течение неограниченного времени в неустойчивом равновесном или метастабильном состоянии. [1] В цифровых логических схемах цифровой сигнал должен находиться в определенных пределах по напряжению или току «0» или «1» , чтобы представлять логический уровень для правильной работы схемы; если сигнал находится в запрещенном промежуточном диапазоне, это может вызвать неправильное поведение логических элементов, к которым применяется сигнал. В метастабильных состояниях схема может быть неспособна перейти на стабильный логический уровень «0» или «1» в течение времени, необходимого для правильной работы схемы. В результате схема может действовать непредсказуемо и может привести к сбою системы, иногда называемому «сбоем». [2] Метастабильность — это пример парадокса Буридана .
Метастабильные состояния являются неотъемлемыми чертами асинхронных цифровых систем и систем с более чем одним независимым тактовым доменом. В самосинхронных асинхронных системах арбитры предназначены для того, чтобы позволить системе продолжить работу только после устранения метастабильности, поэтому метастабильность является нормальным состоянием, а не состоянием ошибки. [3] В синхронных системах с асинхронными входами синхронизаторы спроектированы таким образом, чтобы вероятность сбоя синхронизации была приемлемо малой. [4] Метастабильных состояний можно избежать в полностью синхронных системах, если соблюдены требования к настройке входа и времени удержания на триггерах.
Пример [ править ]

Простой пример метастабильности можно найти в защелке SR NOR , когда оба входа Set и Reset являются истинными (R=1 и S=1), а затем оба переходят в ложное состояние (R=0 и S=0) примерно в одно и то же время. время. Оба выхода Q и Q изначально удерживаются на уровне 0 одновременными входами Set и Reset. После того, как входы Set и Reset станут ложными, триггер (в конечном итоге) перейдет в одно из двух стабильных состояний: одно из Q и Q истинно, а другое ложно. Окончательное состояние будет зависеть от того, какой из R или S первым вернется к нулю в хронологическом порядке, но если оба перейдут примерно в одно и то же время, результирующая метастабильность с промежуточными или колебательными уровнями выходного сигнала может занять сколь угодно много времени, чтобы перейти в стабильное состояние.
Арбитры [ править ]
В электронике арбитр — это схема, предназначенная для определения того, какой из нескольких сигналов поступит первым. Арбитры используются в асинхронных схемах для упорядочения вычислительной деятельности для общих ресурсов и предотвращения одновременных неверных операций. Арбитры используются на входах полностью синхронных систем, а также между тактовыми доменами в качестве синхронизаторов входных сигналов. Хотя они могут свести к минимуму возникновение метастабильности до очень низких вероятностей, все арбитры, тем не менее, имеют метастабильные состояния, которые неизбежны на границах областей входного пространства состояний, что приводит к различным результатам. [5]
Синхронные схемы [ править ]
Методы проектирования синхронных схем позволяют создавать цифровые схемы, устойчивые к режимам отказов, которые могут быть вызваны метастабильностью. Тактовый домен определяется как группа триггеров с общими часами. Такие архитектуры могут формировать схему, гарантированно свободную от метастабильности (ниже определенной максимальной тактовой частоты, выше которой возникает первая метастабильность, а затем полный отказ), предполагая, что общий тактовый сигнал имеет малую асимметрию . Однако даже в этом случае, если система зависит от каких-либо непрерывных воздействий, они, вероятно, будут уязвимы для метастабильных состояний. [6]
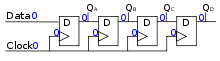
Схемы синхронизатора используются для уменьшения вероятности метастабильности при получении асинхронного входного сигнала или при передаче сигналов между разными тактовыми доменами. Синхронизаторы могут иметь форму каскада D-триггеров (например, сдвиговый регистр на рисунке 3). [7] Хотя каждый этап триггера добавляет дополнительный такт задержки к входному потоку данных, каждый этап предоставляет возможность устранить метастабильность. Такие синхронизаторы можно спроектировать так, чтобы снизить метастабильность до незначительной, но терпимой скорости.
Триггеры Шмитта также можно использовать для снижения вероятности метастабильности, но, как продемонстрировал исследователь Чейни в 1979 году, даже триггеры Шмитта могут стать метастабильными. Он также утверждал, что невозможно полностью исключить возможность метастабильности несинхронизированных входных сигналов в течение конечного времени и что «существует множество теоретических и экспериментальных доказательств того, что область аномального поведения существует для каждого устройства, имеющего два стабильных состояния. " Перед лицом этой неизбежности аппаратное обеспечение может лишь снизить вероятность метастабильности, а системы могут попытаться изящно обрабатывать случайные метастабильные события. [8]
Режимы отказа [ править ]
Хотя метастабильность хорошо изучена и известны архитектурные методы управления ею, она сохраняется как режим отказа в оборудовании.
Серьезные компьютерные и цифровые аппаратные ошибки, вызванные метастабильностью, имеют увлекательную социальную историю. Многие инженеры отказываются верить, что бистабильное устройство может войти в состояние, которое не является ни истинным , ни ложным , и имеет положительную вероятность того, что оно останется неопределенным в течение любого заданного периода времени, хотя и с экспоненциально уменьшающейся вероятностью с течением времени. [9] [10] [11] [12] [13] Однако метастабильность является неизбежным результатом любой попытки отобразить непрерывную область в дискретную. На границах непрерывной области между областями, которые отображаются на разные дискретные выходные данные, точки, произвольно расположенные рядом друг с другом в непрерывной области, отображают различные выходные данные, принимая решение о том, какой выход выбрать, представляет собой сложный и потенциально длительный процесс. [14] Если входные сигналы арбитра или триггера поступают почти одновременно, схема, скорее всего, пересечет точку метастабильности. Метастабильность остается плохо изученной в некоторых кругах, и различные инженеры предложили свои собственные схемы, которые, как утверждается, решают или фильтруют метастабильность; обычно эти схемы просто перемещают возникновение метастабильности из одного места в другое. [15] Микросхемы, использующие несколько источников тактовой частоты, часто тестируются с помощью тестовых тактовых импульсов, которые имеют фиксированные фазовые соотношения, а не с независимыми тактовыми сигналами, дрейфующими друг за другом, которые наблюдаются во время работы. Обычно это явно предотвращает видимость или сообщение о метастабильном режиме отказа, который может возникнуть в полевых условиях. При правильном тестировании на метастабильность часто используются часы с немного разными частотами, что обеспечивает правильную работу схемы.
См. также [ править ]
- Аналого-цифровой преобразователь
- задница Буридана
- Асинхронный процессор
- Отскок земли
- Логика трех состояний
Ссылки [ править ]
- ^ Томас Дж. Чейни и Чарльз Э. Молнар (апрель 1973 г.). «Аномальное поведение схем синхронизатора и арбитра» (PDF) . Транзакции IEEE на компьютерах . С-22 (4): 421–422. дои : 10.1109/TC.1973.223730 . ISSN 0018-9340 . S2CID 12594672 .
- ^ Чейни, Томас Дж. «Моя работа над всем метастабильным, ИЛИ Я и мой сбой» (PDF) . Архивировано из оригинала (PDF) 8 декабря 2015 г. Проверено 5 ноября 2015 г.
- ^ Джон Бейнбридж (2002). Асинхронное межсоединение системы на кристалле . Спрингер. п. 18. ISBN 978-1-85233-598-4 .
- ^ Чейни, Томас Дж . «Перепечатка технического меморандума № 10 «Феномен сбоев» (1966) » . Вашингтонский университет в Сент-Луисе
- ^ Ричард Ф. Тиндер (2009). Проектирование и анализ асинхронных последовательных машин: комплексное развитие проектирования и анализа тактовых независимых конечных автоматов и систем . Издательство Морган и Клейпул. п. 165. ИСБН 978-1-59829-689-1 .
- ^ Климан, Л.; Кантони, А. «Метастабильное поведение в цифровых системах», декабрь 1987 г.. IEEE Design & Test of Computers . 4 (6): 4–19. doi : 10.1109/MDT.1987.295189 . S2CID 1895434 .
- ^ А.П.Дален (19 октября 2023 г.). «Реализация граничного синхронизатора часов в Verilog» . DigiKey Форум электронных компонентов и инженерных решений . Архивировано из оригинала 5 декабря 2023 г. Проверено 17 февраля 2024 г.
- ^ Чейни, Томас (1979). «Комментарии к «Замечаниям о неисправности синхронизатора или блокировки» » . Транзакции IEEE на компьютерах . С-28 (10): 802–804. дои : 10.1109/TC.1979.1675252 . ISSN 0018-9340 .
- ^ Харрис, Сара; Харрис, Дэвид (2015). Цифровой дизайн и компьютерная архитектура: ARM Edition . Морган Кауфманн. стр. 151–153. ISBN 978-0128009116 .
- ^ Гиносар, Ран (2011). «Метастабильность и синхронизаторы: учебное пособие» (PDF) . Центр системных исследований СБИС . Кафедра электротехники и информатики, Технион — Израильский технологический институт, Хайфа. , с. 4-6
- ^ Ксантопулос, Фукидид (2009). Тактирование в современных системах СБИС . Springer Science and Business Media. п. 196. ИСБН 978-1441902610 . , с. 196, 200, экв. 6-29
- ^ «Учебник по метастабильности» (PDF) . Рекомендации по применению АН-219 . Филлипс Полупроводник. 1989 год . Проверено 20 января 2017 г.
- ^ Арора, Мохит (2011). Искусство аппаратной архитектуры: методы и приемы проектирования цифровых схем . Springer Science and Business Media. ISBN 978-1461403975 . , с. 4-5, экв. 1-1
- ^ Лесли Лэмпорт (февраль 2012 г.) [декабрь 1984 г.]. «Принцип Буридана» (PDF) . Проверено 9 июля 2010 г.
- ^ Ран Гиносар. « Четырнадцать способов обмануть ваш синхронизатор » ASYNC 2003.
Внешние ссылки [ править ]
- Метастабильность синхронизированных FIFO
- «Асинхронная» библиография
- Асинхронная логика
- Эффективные самосинхронные интерфейсы для пересечения тактовых доменов
- Доктор Говард Джонсон: Умышленное создание метастабильного состояния
- Подробные пояснения и конструкции синхронизаторов.
- Библиография по метастабильности
- Пересечение тактовой области: замыкание цикла при решении проблем функциональной реализации тактовой области , Cadence Design Systems
- Стивенсон, Дженнифер. Понимание метастабильности в FPGA . Официальный документ корпорации Altera. Июль 2009.
- Бахуханди, Аширвад. Метастабильность. Конспекты лекций по расширенному проектированию логики и теории коммутации. Январь 2002 года.
- Каммингс, Клиффорд Э. Методы синтеза и написания сценариев для проектирования многоасинхронных часов . СНУГ 2001.
- Хаселофф, Эйлхард. Метастабильный отклик в логических схемах с напряжением 5 В. Отчет Texas Instruments. Февраль 1997 года.
- Нистром, Мика и Ален Дж. Мартин. Преодоление синхронного асинхронного разрыва . ВМЭД 2002.
- Патил, Гириш, подразделение БМП, Cadence Design Systems. Проблемы синхронизации часов и методы статической проверки. Техническая конференция Cadence 2004.
- Смит, Майкл Джон Себастьян. Интегральные схемы специального назначения. Аддисон Уэсли Лонгман, 1997 г., глава 6.4.1.
- Штейн, Майк. Пересекая пропасть: асинхронные сигналы в синхронном мире. Особенность дизайна EDN. 24 июля 2003 г.
- Кокс, Джером Р. и Энгель, Джордж Л., Blendics, Inc. Технический документ [1] «Метастабильность и фатальные системные ошибки»], ноябрь 2010 г.
- Адам Тейлор, «Окружение мозга метастабильностью» , EE Times, 20 ноября 2013 г.