Рисование кривых

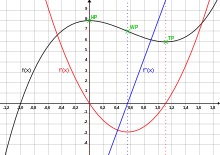
График функции 3 х ³-5 х ²+8 (черный) и его первый (9 х ²-10 x , красный) и вторые (18 x -10, синий) производные . Значение x , при котором *значение y* красной или синей кривой исчезает (становится равным 0), приводит к возникновению локального экстремума (обозначенного «HP», «TP») или точки перегиба («WP») черная кривая соответственно.

В геометрии ) — это метод , зарисовка кривой (или трассировка кривой позволяющий получить приблизительное представление об общей форме плоской кривой с учетом ее уравнения без вычисления большого количества точек, необходимых для подробного графика. Это применение теории кривых для выявления их основных особенностей.

Основные техники

Следующие действия обычно легко выполнить и они дают важные подсказки относительно формы кривой:

Определите точки пересечения x и y кривой. Перехваты x находятся путем установки y равным 0 в уравнении кривой и решения для x . Точно так же точки пересечения y находятся путем установки x равным 0 в уравнении кривой и решения для y .
Определить симметрию кривой. Если показатель степени x всегда четен в уравнении кривой, то ось y является осью симметрии кривой. Аналогично, если показатель степени y в уравнении кривой всегда четный, то ось x является осью симметрии кривой. Если сумма степеней x и y в каждом члене всегда четна или всегда нечетна, то кривая симметрична относительно начала координат , и начало координат называется центром кривой.
Определите любые границы значений x и y .
Если кривая проходит через начало координат, определите там касательные. Для алгебраических кривых это можно сделать, удалив из уравнения все члены, кроме членов самого низкого порядка, и решив его.
Аналогичным образом, удаление из уравнения всех членов, кроме членов высшего порядка, и его решение дают точки, в которых кривая пересекает линию на бесконечности .
Определите асимптоты кривой. Также определите, с какой стороны кривая приближается к асимптотам и где асимптоты пересекают кривую. ^[1]
Приравняйте первую и вторую производные к 0, чтобы найти точки покоя и точки перегиба соответственно. Если уравнение кривой не может быть решено явно для x или y , нахождение этих производных требует неявного дифференцирования .

Диаграмма Ньютона

Диаграмма Ньютона (также известная как параллелограмм Ньютона , в честь Исаака Ньютона ) — это метод определения формы алгебраической кривой вблизи начала координат и вдали от него. Он состоит из построения графиков (α, β) для каждого термина Ax ^аи ^б в уравнении кривой. Полученная диаграмма затем анализируется для получения информации о кривой.

В частности, нарисуйте диагональную линию, соединяющую две точки на диаграмме, так, чтобы все остальные точки находились либо над ней, либо справа и над ней. Существует хотя бы одна такая линия, если кривая проходит через начало координат. Пусть уравнение линии имеет вид q α+ p β= r . Предположим, что кривая аппроксимируется y = Cx ^{цена за квартал} недалеко от источника. Тогда термин Axe ^аи ^б примерно Dx ^α+βp/q. Показатель степени равен r/q , когда (α, β) находится на прямой, и выше, когда он находится выше и правее. Следовательно, согласно этому предположению, значимыми членами вблизи начала координат являются только те члены, которые лежат на прямой, а остальные можно игнорировать; он дает простое приближенное уравнение кривой. Таких диагональных линий может быть несколько, каждая из которых соответствует одной или нескольким ветвям кривой, и приближенные уравнения ветвей можно найти, применяя этот метод поочередно к каждой линии.

Например, лист Декарта определяется уравнением

x^{3}+y^{3}-3axy=0\,

.

Тогда диаграмма Ньютона имеет точки (3, 0), (1, 1) и (0, 3). Можно провести две диагональные линии, как описано выше: 2α+β=3 и α+2β=3. Они производят

x^{2}-3ay=0\,

y^{2}-3ax=0\,

как приближенные уравнения для горизонтальной и вертикальной ветвей кривой, где они пересекаются в начале координат. ^[2]

Аналитический треугольник

Де Гуа расширил диаграмму Ньютона, сформировав метод, называемый аналитическим треугольником (или треугольником де Гуа ). Точки (α, β) наносятся так же, как и в методе диаграмм Ньютона, но добавляется линия α+β= n , где n — степень кривой, чтобы сформировать треугольник, содержащий диаграмму. Этот метод учитывает все линии, ограничивающие наименьший выпуклый многоугольник, содержащий нанесенные точки (см. Выпуклая оболочка ). ^[3]

Приложения

Оптимизация отслеживания в гидродинамике

См. также

Примечание

^ Хилтон (1920 , Глава III §2)
^ Хилтон (1920 , Глава III §3)
^ Фрост (1918 , Глава IX)

Ссылки

Хилтон, Гарольд (1920). «Глава III: Трассировка кривых». Плоские алгебраические кривые . Оксфорд.
Фрост, Персиваль (1918). Элементарный трактат по трассировке кривых . Макмиллан.

Внешние ссылки

Треногин, В.А. (2001) [1994], «Диаграмма Ньютона» , Энциклопедия Математики , EMS Press

[1] Хилтон (1920 , Глава III §2)

[2] Хилтон (1920 , Глава III §3)

[3] Фрост (1918 , Глава IX)

[1]

[2]

[3]