Фолиум Декарта

Лист Декарта (зеленый) с асимптотой (синий), когда $a=1$

В геометрии лист Декарта (от латинского folium « лист »; назван в честь Рене Декарта ) представляет собой алгебраическую кривую, определяемую неявным уравнением

x^{3}+y^{3}-3axy=0.

История [ править ]

Кривая была впервые предложена и изучена Рене Декартом в 1638 году. ^[1] Его претензия на известность связана с одним из инцидентов в развитии исчисления . Декарт предложил Пьеру де Ферма найти касательную к кривой в произвольной точке, поскольку Ферма недавно открыл метод нахождения касательных линий. Ферма легко решил проблему, чего Декарт сделать не смог. ^[2] С момента изобретения математического анализа наклон касательной можно легко найти с помощью неявного дифференцирования . ^[3]

Построение кривой [ править ]

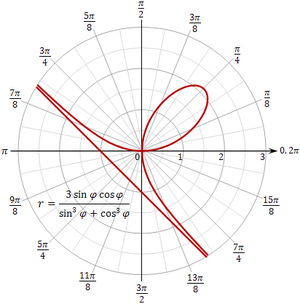
Лист Декарта можно выразить в полярных координатах как

r={\frac {3a\sin \theta \cos \theta }{\sin ^{3}\theta +\cos ^{3}\theta }},

который изображен слева. Это эквивалентно ^[4]

$r={\frac {3a\sec \theta \tan \theta }{1+\tan ^{3}\theta }}.$

Другой метод — написать $y=px$ и решить для $x$ и $y$ с точки зрения $p$ . Это дает рациональные параметрические уравнения : ^[5]

x={{3ap} \over {1+p^{3}}},\,y={{3ap^{2}} \over {1+p^{3}}}.

Мы видим, что параметр связан с положением на кривой следующим образом:

$p<-1$ соответствует $x>0$ , $y<0$ : правое, нижнее, «крыло».
$-1<p<0$ соответствует $x<0$ , $y>0$ : левое, верхнее «крыло».
$p>0$ соответствует $x>0$ , $y>0$ : петля кривой.

Другой способ построения функции может быть получен из симметрии над $y=x$ . Симметрию можно увидеть непосредственно из его уравнения (x и y можно менять местами). Например, применив поворот на 45 ° по часовой стрелке, можно построить функцию, симметричную относительно повернутой оси X.

Эта операция эквивалентна замене:

x={{u+v} \over {\sqrt {2}}},\,y={{u-v} \over {\sqrt {2}}}

и дает

v=\pm u{\sqrt {\frac {3a{\sqrt {2}}-2u}{6u+3a{\sqrt {2}}}}}.

Построение графика в декартовой системе

(u,v)

дает лист, повернутый на 45 ° и, следовательно, симметричный на

u

-ось.

Свойства [ править ]

Он образует петлю в первом квадранте с двойной точкой в начале координат и асимптотой

x+y+a=0\,.

Он симметричен относительно линии

y=x

. Таким образом, они пересекаются в начале координат и в точке

(3a/2,3a/2)

.

Неявное дифференцирование дает формулу для наклона касательной к этой кривой: ^[3]

{\frac {dy}{dx}}={\frac {ay-x^{2}}{y^{2}-ax}}.

Используя любое из приведенных выше полярных представлений, площадь внутренней части петли оказывается равной

3a^{2}/2

. При этом площадь между «крыльями» кривой и ее наклонной асимптотой также равна

3a^{2}/2

. ^[1]

Маклорена трисектрисой Связь с

Лист Декарта связан с трисектрисой Маклорена аффинным преобразованием . Чтобы убедиться в этом, начните с уравнения

x^{3}+y^{3}=3axy\,,

и измените переменные, чтобы найти уравнение в системе координат, повернутой на 45 градусов. Это равнозначно установке

x={{X+Y} \over {\sqrt {2}}},y={{X-Y} \over {\sqrt {2}}}.

В

X,Y

плоскость, уравнение

2X(X^{2}+3Y^{2})=3{\sqrt {2}}a(X^{2}-Y^{2}).

Если мы растянем кривую в $Y$ направлении с коэффициентом ${\sqrt {3}}$ это становится

2X(X^{2}+Y^{2})=a{\sqrt {2}}(3X^{2}-Y^{2}),

которое представляет собой уравнение трисектрисы Маклорена.

Примечания [ править ]

^ Jump up to: Перейти обратно: ^а ^б «Фолиум Декарта» . Энциклопедия математики . 5 июня 2020 г. Проверено 30 января 2021 г.
^ Симмонс, с. 101
^ Jump up to: Перейти обратно: ^а ^б Стюарт, Джеймс (2012). «Раздел 3.5: Неявная дифференциация». Исчисление: ранние трансценденталисты . Соединенные Штаты Америки: Cengage Learning. стр. 209–11. ISBN 978-0-538-49790-9 .
^ Стюарт, Джеймс (2012). «Глава 10: Параметрические уравнения и полярные координаты». Исчисление: ранние трансценденталисты (7-е изд.). Cengage Обучение. п. 687. ИСБН 978-0-538-49790-9 .
^ «DiffGeom3: Параметризованные кривые и алгебраические кривые» . Н. Дж. Уайлдбергер, Университет Нового Южного Уэльса . Архивировано из оригинала 21 декабря 2021 г. Проверено 5 сентября 2013 г.

Ссылки [ править ]

Дж. Деннис Лоуренс: Каталог специальных плоских кривых , 1972, Dover Publications. ISBN 0-486-60288-5 , стр. 106–108.
Джордж Ф. Симмонс : Жемчужины исчисления: краткие жизни и памятная математика , Нью-Йорк, 1992, McGraw-Hill, xiv, 355. ISBN 0-07-057566-5 ; новое издание 2007 г., Математическая ассоциация Америки ( MAA )

Внешние ссылки [ править ]

[:0-1] Jump up to: Перейти обратно: ^а ^б «Фолиум Декарта» . Энциклопедия математики . 5 июня 2020 г. Проверено 30 января 2021 г.

[2] Симмонс, с. 101

[:1-3] Jump up to: Перейти обратно: ^а ^б Стюарт, Джеймс (2012). «Раздел 3.5: Неявная дифференциация». Исчисление: ранние трансценденталисты . Соединенные Штаты Америки: Cengage Learning. стр. 209–11. ISBN 978-0-538-49790-9 .

[4] Стюарт, Джеймс (2012). «Глава 10: Параметрические уравнения и полярные координаты». Исчисление: ранние трансценденталисты (7-е изд.). Cengage Обучение. п. 687. ИСБН 978-0-538-49790-9 .

[5] «DiffGeom3: Параметризованные кривые и алгебраические кривые» . Н. Дж. Уайлдбергер, Университет Нового Южного Уэльса . Архивировано из оригинала 21 декабря 2021 г. Проверено 5 сентября 2013 г.

[1]

[2]

[3]

[4]

[5]