Список спиралей

В этот список спиралей входят названные спирали , описанные математически.

Изображение	Имя	Впервые описано	Уравнение	Комментарий
	круг		$r=k$	Тривиальная спираль
	Архимедова спираль (также арифметическая спираль )	в. 320 г. до н.э.	$r=a+b\cdot \theta$
	Спираль Ферма (также параболическая спираль)	1636	$r^{2}=a^{2}\cdot \theta$
	Спираль Эйлера (также спираль Корню или полиномиальная спираль)	1696	$x(t)=\operatorname {C} (t),\,$$y(t)=\operatorname {S} (t)$	используя интегралы Френеля
	гиперболическая спираль (также обратная спираль )	1704	$r={\frac {a}{\theta }}$
	пляж	1722	$r^{2}\cdot \theta =k$
	логарифмическая спираль (также известная как равноугольная спираль )	1638	$r=a\cdot e^{b\cdot \theta }$	Приближения к этому встречаются в природе.
	Спираль Фибоначчи		дуги окружности, соединяющие противоположные углы квадратов в мозаике Фибоначчи	приближение золотой спирали
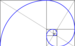
	золотая спираль		$r=\varphi ^{\frac {2\cdot \theta }{\pi }}\,$	частный случай логарифмической спирали
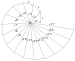	Спираль Теодора (также известная как спираль Пифагора )	в. 500 г. до н.э.	смежные прямоугольные треугольники, состоящие из одного катета единичной длины, а другого катета, являющегося гипотенузой предыдущего треугольника.	приближается к спирали Архимеда
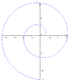	инвольвентировать	1673	$x(t)=r(\cos(t+a)+t\sin(t+a)),$ $y(t)=r(\sin(t+a)-t\cos(t+a))$	развертки круга выглядят как спирали Архимеда.
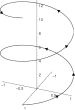	спираль		$r(t)=1,\,$ $\theta (t)=t,\,$ $z(t)=t$	трехмерная спираль
	Румбовидная линия (также локсодромия)			тип спирали, нарисованной на сфере
	Спираль Котса	1722	${\frac {1}{r}}={\begin{cases}A\cosh(k\theta +\varepsilon )\\A\exp(k\theta +\varepsilon )\\A\sinh(k\theta +\varepsilon )\\A(k\theta +\varepsilon )\\A\cos(k\theta +\varepsilon )\\\end{cases}}$	Решение задачи двух тел для центральной силы обратного куба
	Спирали Пуансо		$r=a\cdot \operatorname {csch} (n\cdot \theta ),\,$ $r=a\cdot \operatorname {sech} (n\cdot \theta )$
	спираль Нильсена	1993	$x(t)=\operatorname {ci} (t),\,$ $y(t)=\operatorname {si} (t)$	Вариант спирали Эйлера с использованием интегралов синуса и косинуса.
	Многоугольная спираль			частный случай аппроксимации логарифмической спирали
	Спираль Фрейзера	1908		Оптическая иллюзия на основе спиралей
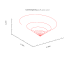	Конхоспираль		$r=\mu ^{t}\cdot a,\,$$\theta =t,\,$$z=\mu ^{t}\cdot c$	трехмерная спираль на поверхности конуса.
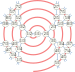	Спираль Калкина – Уилфа
	Спираль Улама (также первичная спираль)	1963
	Спираль Сака	1994		вариант спирали Улама и спирали Архимеда.
	Спираль Зейферта	2000	$r=\operatorname {sn} (s,k),\,$$\theta =k\cdot s$$z=\operatorname {cn} (s,k)$	спиральная кривая на поверхности сферы используя эллиптические функции Якоби
	Трактрикс спираль	1704	${\begin{cases}r=A\cos(t)\\\theta =\tan(t)-t\end{cases}}$
	Спираль Паппа	1779	${\begin{cases}r=a\theta \\\psi =k\end{cases}}$	3D коническая спираль, изученная Паппом и Паскалем
	допплеровская спираль		$x=a\cdot (t\cdot \cos(t)+k\cdot t),\,$$y=a\cdot t\cdot \sin(t)$	2D-проекция спирали Паппа
	Захват спирали		$x={\frac {\sin(t)}{t}}-2\cdot \cos(t)-t\cdot \sin(t),\,$$y=-{\frac {\cos(t)}{t}}-2\cdot \sin(t)+t\cdot \cos(t)$	Кривая, имеющая катакаустику, образующую круг. Аппроксимирует спираль Архимеда.
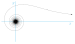
	Атомная спираль	2002	$r={\frac {\theta }{\theta -a}}$	Эта спираль имеет две асимптоты ; один - это круг радиуса 1, а другой - линия $\theta =a$
	Галактическая спираль	2019	${\begin{cases}dx=R\cdot {\frac {y}{\sqrt {x^{2}+y^{2}}}}d\theta \\dy=R\cdot \left[\rho (\theta )-{\frac {x}{\sqrt {x^{2}+y^{2}}}}\right]d\theta \end{cases}}{\begin{cases}x=\sum dx\\\\\\y=\sum dy+R\end{cases}}$	Дифференциальные спиральные уравнения были разработаны для моделирования спиральных рукавов дисковых галактик и имеют 4 решения с тремя различными случаями: $\rho <1,\rho =1,\rho >1$спиральные узоры определяются поведением параметра $\rho$. Для $\rho <1$, спирально-кольцевой узор; $\rho =1,$ обычная спираль; $\rho >1,$ свободная спираль. R — расстояние от начальной точки спирали (0, R) до центра. Вычисленные x и y необходимо повернуть назад на ( $-\theta$) для построения графиков.

См. также

• Екатерининское колесо (фейерверк)
• Список спиральных галактик
• Спираль Паркера
• Спирангл
• Спирограф