Предгрупповая грамматика

Предгрупповая грамматика (ПГ) — это грамматический формализм, тесно связанный с категориальными грамматиками . Подобно категориальной грамматике (CG), PG — это своего рода тип логической грамматики . Однако, в отличие от CG, PG не имеет выделенного типа функции. Скорее, PG использует обратные типы в сочетании с моноидальной операцией.

Определение прегруппы

Предгруппа — это частично упорядоченная алгебра. $(A,1,\cdot ,-^{l},-^{r},\leq )$ такой, что $(A,1,\cdot )$ является моноидом , удовлетворяющим следующим соотношениям:

• $x^{l}\cdot x\leq 1\qquad x\cdot x^{r}\leq 1$ (сокращение)
• $1\leq x\cdot x^{l}\qquad 1\leq x^{r}\cdot x$ (расширение)

Соотношения сжатия и расширения иногда называют законами Айдукевича .

Отсюда можно доказать, что выполняются следующие уравнения:

• $1^{l}=1=1^{r}$
• $x^{lr}=x=x^{rl}$
• $(x\cdot y)^{l}=y^{l}\cdot x^{l}\qquad (x\cdot y)^{r}=y^{r}\cdot x^{r}$

$x^{l}$ и $x^{r}$ называются левым и правым сопряженными x соответственно .

Символы $\cdot$ и $\leq$ также написаны $\otimes$ и $\to$ соответственно. В теории категорий предгруппы также известны как автономные категории. или (несимметричные) компактные замкнутые категории . Более типично, $x\cdot y$ будет просто представлено смежностью, т.е. как $xy$.

грамматики

Грамматика предгруппы состоит из словаря слов (и, возможно, морфем ) L , набора атомарных типов T , который свободно порождает предгруппу, и отношения $:$ который связывает слова с типами. В простых грамматиках предгрупп типизация — это функция, которая сопоставляет слова только одному типу каждое.

Примеры

Несколько простых, интуитивно понятных примеров использования английского языка в качестве языка моделирования демонстрируют основные принципы, лежащие в основе предгрупп и их использования в лингвистических областях.

Пусть L = { Джон, Мэри, собака, кошка, встретил, залаял, в }, пусть T = { N, S, N ₀ } и пусть выполняется следующее отношение типизации:

${\textit {John}}:N\qquad {\textit {Mary}}:N\qquad {\textit {the}}:N\cdot N_{0}^{l}\qquad {\textit {dog}}:N_{0}\qquad {\textit {cat}}:N_{0}$

${\textit {met}}:N^{r}\cdot S\cdot N^{l}\qquad {\textit {barked}}:N^{r}\cdot S\qquad {\textit {at}}:S^{r}\cdot N^{rr}\cdot N^{r}\cdot S\cdot N^{l}$

Предложение S , имеющее тип T, называется грамматическим, если $T\leq S$. Мы можем доказать это, используя цепочку $\leq$. Например, мы можем доказать, что ${\textit {John}}\ {\textit {met}}\ {\textit {Mary}}:N\cdot N^{r}\cdot S\cdot N^{l}\cdot N$ является грамматическим, доказывая, что $N\cdot N^{r}\cdot S\cdot N^{l}\cdot N\leq S$:

$N\cdot N^{r}\cdot S\cdot N^{l}\cdot N~\leq ~S\cdot N^{l}\cdot N~\leq ~S$

сначала используя сокращение на $N\cdot N^{r}$ а потом еще раз $N^{l}\cdot N$. Однако существует более удобное обозначение, обозначающее сокращения путем соединения их нарисованной связью между типами сокращения (при условии, что ссылки вложены, т. е. не пересекаются). Слова также обычно располагаются над их типами, чтобы сделать доказательство более интуитивным. То же доказательство в этих обозначениях просто

Более сложный пример доказывает, что собака залаяла на кошку грамматически:

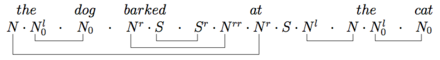
Исторические заметки

Предгрупповые грамматики были введены Иоахимом Ламбеком в 1993 году как развитие его синтаксического исчисления , заменяющего частное сопряженными. Такие сопряженные уже использовались Харрисом ранее , но без повторных сопряжений и правил расширения.Добавление таких прилагательных было интересно для обработки более сложных лингвистических случаев, когда тот факт, что $a^{ll}\neq a$ необходим. Это также было мотивировано более алгебраической точкой зрения: определение предгруппы является ослаблением определения группы , вводя различие между левыми и правыми инверсиями и заменяя равенство порядком. Это ослабление было необходимо, поскольку использование типов из свободной группы не сработало: прилагательное получило бы тип $N\cdot N^{-1}=1$, следовательно, его можно вставить в любую позицию предложения.

Затем были определены и изучены предгрупповые грамматики для различных языков (или их фрагментов), включая английский , Итальянский , Французский , персидский и санскрит . Языки с относительно свободным порядком слов, такие как санскрит, требовали введения коммутационных отношений в предгруппу, используя прецикличность.

Семантика предгрупповых грамматик

Из-за отсутствия типов функций в PG обычный метод задания семантики через λ-исчисление или через обозначения функций недоступен каким-либо очевидным способом. Вместо этого существуют два разных метода: один чисто формальный метод, соответствующий λ-исчислению, и один денотационный метод, аналогичный (фрагменту) тензорной математики квантовой механики .

Чисто формальная семантика

Чисто формальная семантика PG состоит из логического языка, определенного в соответствии со следующими правилами:

• Учитывая набор атомарных термов T = { a , b , ...} и атомарных функциональных символов F = { f _m , g _n , ...} (где индексы представляют собой мета-нотации, указывающие арность), а также переменные x , y , ..., все константы, переменные и правильно сформированные приложения функций являются базовыми терминами (приложение функции правильно сформировано, когда символ функции применяется к соответствующему количеству аргументов, которые могут быть получены из атомарных терминов, переменных или могут быть другими основными терминами)
• Любой базовый термин является термином
• Учитывая любую переменную x , [ x ] является термином
• Учитывая любые члены m и n , $m\cdot n$ это термин

Некоторые примеры терминов: f ( x ), g ( a , h ( x , y )), $g(x,b)\cdot [x]$. Переменная x является свободной в терме t, если [ x ] не появляется в t , а терм без свободных переменных является закрытым термом. Термины можно набирать с помощью типов предгрупп очевидным образом.

Применяются обычные соглашения относительно α-преобразования.

Для данного языка мы даем задание I , которое отображает типизированные слова в типизированные закрытые термины таким образом, чтобы соблюдалась предгрупповая структура типов. Таким образом, для приведенного выше английского фрагмента мы могли бы иметь следующее присвоение (с очевидным, неявным набором атомарных терминов и функциональных символов):

${\begin{aligned}I({\textit {John}}:N)&=j:E\\I({\textit {Mary}}:N)&=m:E\\I(the:N\cdot N_{0}^{l})&=\iota (p)\cdot [p]:E\cdot E_{0}^{l}\\I(dog:N_{0})&=dog:E_{0}\\I(cat:N_{0})&=cat:E_{0}\\I(met:N^{r}\cdot S\cdot N^{l})&=[x]\cdot met(x,y)\cdot [y]:E^{r}\cdot T\cdot E^{l}\\I(barked:N^{r}\cdot S)&=[x]\cdot barked(x):E^{r}\cdot T\\I(at:S^{r}\cdot N^{rr}\cdot N^{r}\cdot S\cdot N^{l})&=[x]\cdot y\cdot [y]\cdot at(x,z)\cdot [z]:T^{r}\cdot E^{rr}\cdot E^{r}\cdot T\cdot E^{l}\end{aligned}}$

где E — тип сущностей в области, а T — тип значений истинности.

Вместе с этим основным определением семантики PG у нас также есть правила редукции, которые используются параллельно с редукцией типов. Разместив синтаксические типы вверху, а семантику внизу, мы имеем

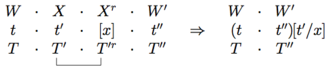
Например, применив это к типам и семантике предложения ${\textit {John}}\ {\textit {met}}\ {\textit {Mary}}:N\cdot (N^{r}\cdot S\cdot N^{l})\cdot N$ (подчеркивая, что ссылка сокращается)

Для предложения ${\textit {the}}\ {\textit {dog}}\ {\textit {barked}}\ {\textit {at}}\ {\textit {the}}\ {\textit {cat}}:(N\cdot N_{0}^{l})\cdot N_{0}\cdot (N^{r}\cdot S)\cdot (S^{r}\cdot N^{rr}\cdot N^{r}\cdot S\cdot N^{l})\cdot (N\cdot N_{0}^{l})\cdot N_{0}$:

См. также

• Компактная закрытая категория
• Мягкое исчисление

Ссылки

• Ламбек, Иоахим (2008). «Грамматики предгрупп и самые ранние примеры Хомского» (PDF) . Журнал логики, языка и информации . 17 (2): 141–160. дои : 10.1007/s10849-007-9053-2 . S2CID   30256603 .
• Преллер, Анна (2007). «Семантические грамматики предгрупп обрабатывают зависимости на больших расстояниях во французском языке» (PDF) . Рукопись .
• Клаудия Касадио (2004), Грамматика предгруппы. Теория и приложения