Фокальные коники
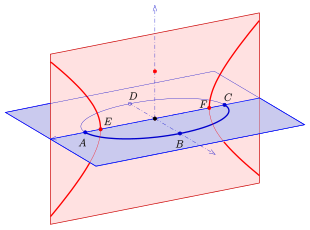
A,C: вершины эллипса и фокусы гиперболы.
E,F: фокусы эллипса и вершины гиперболы.

A: вершина красной параболы и фокус синей параболы.
F: фокус красной параболы и вершина синей параболы.
В геометрии из фокальные коники — это пара кривых, состоящих [1] [2] или
- эллипс . и гипербола , где гипербола содержится в плоскости, ортогональной плоскости, содержащей эллипс Вершины гиперболы являются фокусами эллипса, а ее фокусы - вершинами эллипса (см. схему).
или
- две параболы , которые содержатся в двух ортогональных плоскостях и вершина одной параболы является фокусом другой и наоборот.
Фокальные коники играют существенную роль, отвечая на вопрос: «Какие правые круговые конусы содержат данный эллипс, гиперболу или параболу (см. ниже)».
Фокальные коники используются в качестве направляющих для создания циклид Дюпена в качестве поверхностей каналов двумя способами. [3] [4]
Фокальные коники можно рассматривать как вырожденные фокальные поверхности : циклиды Дюпена - единственные поверхности, у которых фокальные поверхности схлопываются в пару кривых, а именно фокальные коники. [5]
В физической химии фокальные коники используются для описания геометрических свойств жидких кристаллов . [6]
Не следует смешивать фокальные коники с конфокальными кониками . Последние имеют все те же очаги.
Уравнения и параметрические представления
[ редактировать ]Эллипс и гипербола
[ редактировать ]- Уравнения
Если описать эллипс в плоскости xy обычным способом уравнением
то соответствующая фокальная гипербола в плоскости xz имеет уравнение
где - линейный эксцентриситет эллипса с
- Параметрические представления
- эллипс: и
- гипербола:
Две притчи
[ редактировать ]Две параболы в плоскости xy и в плоскости xz:
- 1. парабола: и
- 2. парабола:
с полуправая часть обеих парабол.
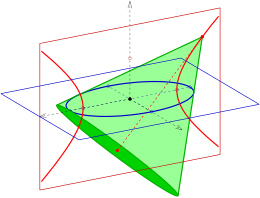
Правильные круговые конусы через эллипс
[ редактировать ]- Вершины правых круговых конусов, проходящих через данный эллипс, лежат на фокальной гиперболе, принадлежащей эллипсу.
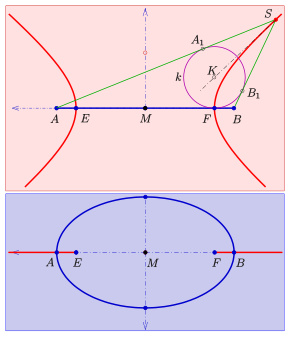
- Доказательство
Дано : Эллипс с вершинами. и очаги и правильный круговой конус с вершиной содержащий эллипс (см. диаграмму).
Из-за симметрии ось конуса должна находиться в плоскости, проходящей через фокусы, ортогональной плоскости эллипса. Существует сфера Одуванчика , который касается плоскости эллипса в фокусе и конус в круге. Из диаграммы и того факта, что все касательные расстояния точки к сфере равны, получаем:
Следовательно:
- константа
и множество всех возможных вершин лежит на гиперболе с вершинами и фокусы .
Аналогично доказываются случаи, когда конусы содержат гиперболу или параболу. [7]
Ссылки
[ редактировать ]- ^ Мюллер-Круппа, стр. 104.
- ^ Glaeser-Stachel-Odehnal, с. 137
- ^ Феликс Кляйн: Лекции по высшей геометрии , редакторы: В. Блашке, Рихард Курант, Springer-Verlag, 2013, ISBN 3642498485 , С. 58.
- ^ Глезер-Штахель-Оденаль: с. 147
- ^ Д. Гильберт, С. Кон-Воссен: Геометрия и воображение , Chelsea Publishing Company, 1952, стр. 218.
- ^ Томас Эндрю Вэй: Физика живых процессов , Verlag John Wiley & Sons, 2014, ISBN 1118698274 , с. 128.
- ^ Глезер-Штахель-Оденаль с. 139
- Георг Глезер, Хельмут Шванц, Борис Оденал: Вселенная коников , Springer, 2016, ISBN 3662454505 .
- Э. Мюллер, Э. Круппа : Учебник по выполнению геомелии , Springer-Verlag, Вена, 1961, ISBN 978-3-211-80589-3 .
















