Материал Кельвина – Фойгта

Материал Кельвина -Фойгта , также называемый материалом Фойгта , представляет собой наиболее простую модель вязкоупругого материала, демонстрирующую типичные эластичные свойства. Он чисто эластичен в длительных периодах времени (медленная деформация), но проявляет дополнительную устойчивость к быстрой деформации. Модель была разработана независимо британским физиком лордом Кельвином . ^[1] в 1865 году немецким физиком Вольдемаром Фойгтом. ^[2] в 1890 году. ^[3]

Определение

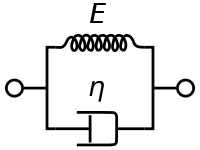
Модель Кельвина-Фойгта, также называемая моделью Фойгта, представлена чисто вязким демпфером и чисто упругой пружиной, соединенными параллельно, как показано на рисунке.

Если вместо этого мы соединим эти два элемента последовательно, мы получим модель материала Максвелла .

Поскольку два компонента модели расположены параллельно, деформации в каждом компоненте одинаковы:

\varepsilon _{\text{Total}}=\varepsilon _{\rm {S}}=\varepsilon _{\rm {D}}.

где индекс D указывает на напряжение-деформацию в демпфере, а индекс S указывает на напряжение-деформацию в пружине. Аналогично, общее напряжение будет представлять собой сумму напряжений в каждом компоненте: ^[4]

\sigma _{\text{Total}}=\sigma _{\rm {S}}+\sigma _{\rm {D}}.

Из этих уравнений мы получаем, что в материале Кельвина – Фойгта напряжение σ , деформация ε и их скорость изменения во времени t определяются уравнениями вида:

\sigma (t)=E\varepsilon (t)+\eta {\frac {d\varepsilon (t)}{dt}},

или, в точечной записи:

\sigma =E\varepsilon +\eta {\dot {\varepsilon }},

где E — модуль упругости , а $\eta$ это вязкость . Уравнение можно применить либо к напряжению сдвига , либо к нормальному напряжению материала.

Последствия внезапного стресса

Зависимость безразмерной деформации от безразмерного времени при постоянном напряжении

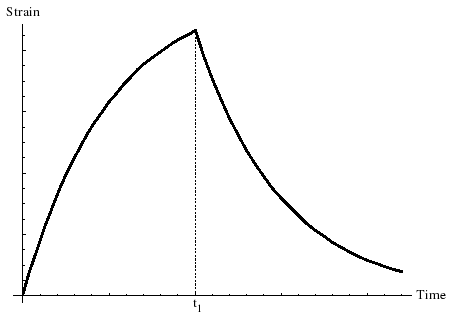
Если мы внезапно приложим какой-то постоянный стресс $\sigma _{0}$ к материалу Кельвина – Фойгта, то деформации будут приближаться к деформации чисто упругого материала. $\sigma _{0}/E$ разница убывает экспоненциально: ^[4]

\varepsilon (t)={\frac {\sigma _{0}}{E}}(1-e^{-t/\tau _{R}}),

где t - время и $\tau _{R}={\frac {\eta }{E}}$ это время замедления .

Если бы мы освободили материал вовремя $t_{1}$ , то упругий элемент будет тормозить материал обратно до тех пор, пока деформация не станет нулевой. Замедление подчиняется следующему уравнению:

\varepsilon (t>t_{1})=\varepsilon (t_{1})e^{-(t-t_{1})/\tau _{R}}.

На рисунке представлена зависимость безразмерной деформации ${\frac {E\varepsilon (t)}{\sigma _{0}}}$ в безразмерное время $t/\tau _{R}$ . На снимке нагрузка на материал нагружена во времени. $t=0$ , и выпущенный в более позднее безразмерное время $t_{1}^{*}=t_{1}/\tau _{R}$ .

Поскольку все деформации обратимы (хотя и не внезапно), материал Кельвина-Фойгта является твердым .

Модель Фойгта предсказывает ползучесть более реалистично, чем модель Максвелла, потому что в бесконечном временном интервале деформация приближается к константе:

\lim _{t\to \infty }\varepsilon ={\frac {\sigma _{0}}{E}},

в то время как модель Максвелла предсказывает линейную зависимость между деформацией и временем, что чаще всего не соответствует действительности. Хотя модель Кельвина-Фойгта эффективна для прогнозирования ползучести, она не подходит для описания релаксационного поведения после снятия стрессовой нагрузки.

Динамический модуль

Комплексный динамический модуль материала Кельвина – Фойгта определяется выражением:

E^{\star }(\omega )=E_{0}(1+i\omega \tau ).

Таким образом, действительная и мнимая составляющие динамического модуля называются модулем упругости. $E^{\prime }$ и $E^{\prime \prime }$ соответственно:

E^{\prime }=\Re [E^{\star }(\omega )],

E^{\prime \prime }=\Im [E^{\star }(\omega )]=E_{0}\omega \tau .

Обратите внимание, что $E^{\prime }$ является постоянным, в то время как $E^{\prime \prime }$ прямо пропорциональна частоте (где масштаб времени $\tau$ – константа пропорциональности). Часто эта константа $\tau$ умноженный на угловую частоту $\omega$ называется модулем потерь $\eta =\omega \tau$ .

Ссылки

^ «IV. Об упругости и вязкости металлов» . Труды Лондонского королевского общества . 14 : 289–297. 1865-12-31. дои : 10.1098/rspl.1865.0052 . ISSN 0370-1662 .
^ Фойгт, Вольдемар (1890). «О внутреннем трении твердых тел, особенно кристаллов» . Трактаты Королевского общества наук в Геттингене (на немецком языке). 36 :3-47.
^ Раджагопал, КР (2009 г.). «Заметка о переоценке и обобщении модели Кельвина – Фойгта» . Коммуникации по исследованиям в области механики . 36 (2): 232–235. дои : 10.1016/j.mechrescom.2008.09.005 .
^ Перейти обратно: ^а ^б Мейерс, Марк Андре; Чавла, Кришан Кумар (1999). «Раздел 13.11». Механическое поведение материалов . Издательство Кембриджского университета. стр. 570–580. ISBN 978-1-107-39418-6 .

См. также

[1] «IV. Об упругости и вязкости металлов» . Труды Лондонского королевского общества . 14 : 289–297. 1865-12-31. дои : 10.1098/rspl.1865.0052 . ISSN 0370-1662 .

[2] Фойгт, Вольдемар (1890). «О внутреннем трении твердых тел, особенно кристаллов» . Трактаты Королевского общества наук в Геттингене (на немецком языке). 36 :3-47.

[3] Раджагопал, КР (2009 г.). «Заметка о переоценке и обобщении модели Кельвина – Фойгта» . Коммуникации по исследованиям в области механики . 36 (2): 232–235. дои : 10.1016/j.mechrescom.2008.09.005 .

[:0-4] Перейти обратно: ^а ^б Мейерс, Марк Андре; Чавла, Кришан Кумар (1999). «Раздел 13.11». Механическое поведение материалов . Издательство Кембриджского университета. стр. 570–580. ISBN 978-1-107-39418-6 .

[1]

[2]

[3]

[4]