Полулогарифмический график

Логарифмически-линейный тип полулогарифмического графика, определяемый логарифмическим масштабом по оси y (вертикальным) и линейным масштабом по оси x (горизонтальным). На графике показаны линии: y = 10. ^х (красный), y = x (зеленый), y = log( x ) (синий).

Линейно-логарифмический тип полулогарифмического графика, определяемый логарифмическим масштабом по оси x и линейным масштабом по оси y. На графике показаны линии: y = 10. ^х (красный), y = x (зеленый), y = log( x ) (синий).

В науке и технике полулогарифмический график / график или полулогарифмический график / график имеют одну ось в логарифмическом масштабе , другую в линейном масштабе . Это полезно для данных с экспоненциальными отношениями, когда одна переменная охватывает большой диапазон значений.

Все уравнения вида $y=\lambda a^{\gamma x}$ образуют прямые линии при полулогарифмическом построении, поскольку взятие журналов обеих сторон дает

$\log _{a}y=\gamma x+\log _{a}\lambda .$

Это линия с наклоном $\gamma$ и $\log _{a}\lambda$ вертикальный перехват. Логарифмическая шкала обычно обозначается по основанию 10; иногда в базе 2:

$\log(y)=(\gamma \log(a))x+\log(\lambda ).$

Логарифмически -линейный (иногда логарифмический) график имеет логарифмический масштаб по оси y и линейный масштаб по оси x ; линейный -логарифм (иногда лин-логарифм) является противоположностью. Именование — выход-вход ( y – x ), порядок, противоположный ( x , y ).

На полулогарифмическом графике интервал шкалы по оси Y (или оси X ) пропорционален логарифму числа, а не самому числу. Это эквивалентно преобразованию значений y (или значений x ) в их журнал и построению графика данных в линейных масштабах. Логарифмический график использует логарифмический масштаб для обеих осей и, следовательно, не является полулогарифмическим графиком.

Уравнения

Уравнение линии на линейно-логарифмическом графике, где ось абсцисс масштабируется логарифмически (с логарифмическим основанием n ), будет иметь вид

$F(x)=m\log _{n}(x)+b.\,$

Уравнение линии на логарифмически-линейном графике с логарифмически масштабированной осью ординат (с логарифмическим основанием n ) будет выглядеть следующим образом:

$\log _{n}(F(x))=mx+b$

$F(x)=n^{mx+b}=(n^{mx})(n^{b}).$

Нахождение функции по полулогарифмическому графику

Линейно-логарифмический график

На линейно-логарифмическом графике выберите некоторую фиксированную точку ( x ₀ , F ₀ ), где F ₀ является сокращением от F ( x ₀ ), где-нибудь на прямой линии на приведенном выше графике, а затем какую-нибудь другую произвольную точку ( x ₁ , F ₁ ) на том же графике. Формула наклона графика:

$m={\frac {F_{1}-F_{0}}{\log _{n}(x_{1}/x_{0})}}$

что приводит к

$F_{1}-F_{0}=m\log _{n}(x_{1}/x_{0})$

или

$F_{1}=m\log _{n}(x_{1}/x_{0})+F_{0}=m\log _{n}(x_{1})-m\log _{n}(x_{0})+F_{0}$

это означает, что $$F(x)=m\log _{n}(x)+\mathrm {constant}$$

Другими словами, F пропорционально логарифму x , умноженному на наклон прямой линии линейно-логарифмического графика, плюс константа. В частности, прямая линия на линейно-логарифмическом графике, содержащая точки ( F ₀ , x ₀ ) и ( F ₁ , x ₁ ), будет иметь функцию:

$F(x)=(F_{1}-F_{0}){\left[{\frac {\log _{n}(x/x_{0})}{\log _{n}(x_{1}/x_{0})}}\right]}+F_{0}=(F_{1}-F_{0})\log _{\frac {x_{1}}{x_{0}}}{\left({\frac {x}{x_{0}}}\right)}+F_{0}$

логарифмически-линейный график

На логарифмическом графике (логарифмический масштаб по оси y) выберите некоторую фиксированную точку ( x ₀ , F ₀ ), где F ₀ является сокращением от F ( x ₀ ), где-то на прямой линии на графике выше. и далее какая-нибудь другая произвольная точка ( x ₁ , F ₁ ) на том же графике. Формула наклона графика:

$m={\frac {\log _{n}(F_{1}/F_{0})}{x_{1}-x_{0}}}$

что приводит к

$\log _{n}(F_{1}/F_{0})=m(x_{1}-x_{0})$

Обратите внимание, что н ^{журнал _п ( F ₁ )} = Ф ₁ . Таким образом, журналы можно инвертировать, чтобы найти:

${\frac {F_{1}}{F_{0}}}=n^{m(x_{1}-x_{0})}$

или

$F_{1}=F_{0}n^{m(x_{1}-x_{0})}$

Это можно обобщить для любой точки, а не только для F ₁ :

$F(x)={F_{0}}n^{\left({\frac {x-x_{0}}{x_{1}-x_{0}}}\right)\log _{n}(F_{1}/F_{0})}$

Реальные примеры

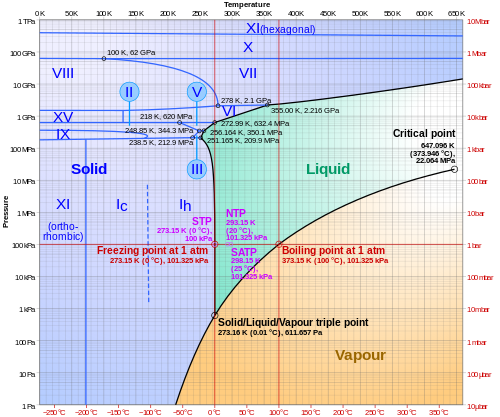
Фазовая диаграмма воды

В физике и химии график зависимости давления от температуры можно использовать для иллюстрации различных фаз вещества, как, например, для воды :

логарифмическая – линейная фазовая диаграмма давление–температура воды. Римские цифры обозначают различные фазы льда .

Развитие «свиного гриппа» в 2009 г.

Хотя десять является наиболее распространенным основанием , бывают случаи, когда более уместны другие основания, как в этом примере:

Полулогарифмический график случаев заболевания и смертности во время вспышки гриппа А (H1N1) в 2009 г.

Обратите внимание, что в то время как горизонтальная ось (время) является линейной, с датами, расположенными на равном расстоянии друг от друга, вертикальная ось (случаи) является логарифмической, причем равномерно расположенные деления помечены последовательными степенями двойки. На полулогарифмическом графике легче увидеть, когда инфекция перестала распространяться с максимальной скоростью (т.е. прямая линия на этом экспоненциальном графике) и начинает изгибаться, указывая на более медленную скорость. Это может указывать на то, что какая-то форма мер по смягчению последствий работает, например, социальное дистанцирование.

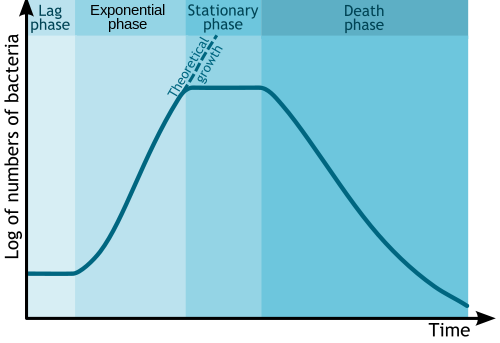
Микробный рост

В биологии и биологической инженерии изменение численности микробов из-за бесполого размножения и истощения питательных веществ обычно иллюстрируется полулогарифмическим графиком. логарифм числа или массы бактерий Время обычно является независимой осью, а в качестве зависимой переменной используется или других микробов. Это формирует график с четырьмя отдельными фазами, как показано ниже.

Кривая роста бактерий

См. также

• Номограмма , более сложные графики
• Нелинейная регрессия#Преобразование для преобразования нелинейной формы в полулогарифмическую форму, поддающуюся неитеративным вычислениям.
• Логарифмический график