Треугольники 5-Con

Наименьшие 5-конечные треугольники с целыми сторонами.

В геометрии два треугольника называются 5-Con или почти конгруэнтными, если они не являются конгруэнтными треугольниками , но являются подобными треугольниками и имеют две общие длины сторон (несоответствующих сторон). Треугольники 5-Con являются важными примерами для понимания решения треугольников . Действительно, знания трех углов и двух сторон (но не их последовательности) недостаточно для определения треугольника с точностью до сравнения. Треугольник называется способным к 5-Con, если существует другой треугольник, почти конгруэнтный ему.

Треугольники 5-Con обсуждались Поли: а позже Джонс и Петерсон. О них кратко упоминает Мартин Гарднер в своей книге «Математический цирк». Еще одна ссылка - следующее упражнение

Объясните, как два треугольника могут иметь пять частей (сторон, углов) одного треугольника, конгруэнтных пяти частям другого треугольника, но не быть конгруэнтными треугольниками.

Подобное учение датируется 1955 годом. и там упоминается более ранняя ссылка. Однако невозможно датировать первое появление таких стандартных упражнений с треугольниками.

Примеры

Существует бесконечно много пар треугольников 5-Con, вплоть до масштабирования.

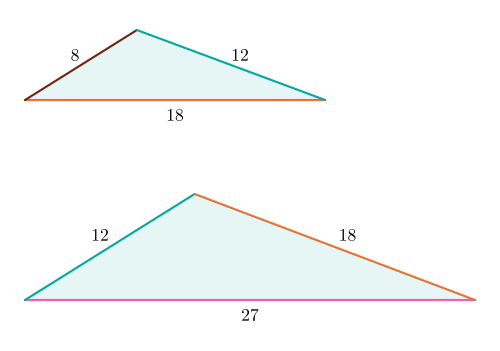
• Наименьшие треугольники 5-Con с целыми сторонами имеют длины сторон (8; 12; 18) и (12; 18; 27). Это пример с тупоугольными треугольниками .
• Примером остроугольных треугольников 5-Con являются (1000; 1100; 1210) и (1100; 1210; 1331).
• 5-Con Прямоугольные треугольники — это в точности те треугольники, которые получены в результате масштабирования пары $(1;m;m^{2})$ и $(m;m^{2};m^{3})$ с $m={\sqrt {\frac {1+{\sqrt {5}}}{2}}}={\sqrt {\phi }}$ где φ — золотое сечение . Следовательно, это треугольники Кеплера и не может быть прямых 5-Con треугольников с целыми сторонами.
• Не существует равносторонних или равнобедренных треугольников с 5-Con , потому что для этого потребуется m = 1, а треугольники с 5-Con были бы конгруэнтны.
• Не существует целочисленных треугольников с 5-Con, которые были бы героновскими, поскольку стороны целочисленных треугольников с 5-Con находятся в геометрической прогрессии.

Результаты

1. Рассмотрим треугольники 5-Con с длинами сторон $(a;b;c)$ и $(ma;mb;mc)$ где $m$ - коэффициент масштабирования, который, как мы можем предположить, больше, чем $1$. Мы также можем предположить $a\leq b\leq c$. Тогда мы должны иметь $b=ma$ и $c=mb$. Тогда две тройки длин сторон имеют вид: $$a(1;m;m^{2})\qquad \mathrm {and} \qquad a(m;m^{2};m^{3}).$$И наоборот, для любого $a>0$ и $1<m<{\frac {1+{\sqrt {5}}}{2}}$, такие тройки являются длинами сторон треугольников с 5 Con. (Предполагая без ограничения общности, что $a=1$, наибольшее число в первой тройке равно $m^{2}$ и нам нужно только обеспечить $m^{2}<1+m$; вторая тройка получается из первой путем масштабирования с $m$. Итак, у нас есть два треугольника: они явно подобны и ровно две из трех длин сторон совпадают.) Некоторые ссылки работают с $m^{-1}<1$ вместо этого, что приводит к неравенствам ${\frac {{\sqrt {5}}-1}{2}}<m^{-1}<1$.

2. Любой треугольник, поддерживающий 5-Con, имеет разные длины сторон, а средняя является средним геометрическим двух других. Тогда отношение длины наибольшей и средней стороны будет равно соотношению длины средней и наименьшей стороны. Мы можем использовать как это соотношение, так и обратное ему для масштабирования и получения почти конгруэнтного треугольника.

Треугольники 5-Con с одинаковой наибольшей стороной.

3. Для изучения возможных форм треугольников 5-Con можно ограничиться изучением треугольников с длинами сторон $$(1;m;m^{2})\qquad \mathrm {where} \qquad 1<m<{\frac {1+{\sqrt {5}}}{2}}.$$Наибольший угол является строго возрастающей непрерывной функцией от $m$ и изменяется от 60° до 180° (исключаются предельные случаи). Прямоугольный треугольник соответствует значению $m={\sqrt {\frac {1+{\sqrt {5}}}{2}}}$. Для удобства масштабируем треугольник так, чтобы получить $(m^{-2};m^{-1};1)$, так что наибольшая сторона зафиксирована: тогда противоположная вершина перемещается по кривой как $m$ варьируется, как показано на рисунке.

4. Наличие двух треугольников 5-Con с целыми сторонами равносильно (в приведенных выше обозначениях) взятию любого рационального числа. $1<m<{\frac {1+{\sqrt {5}}}{2}}$ а затем выбирая $a>0$ таким образом, что $am^{3}$является целым числом. В четырех из них задействованы целые длины сторон. $(a;am;am^{2};am^{3})$ не имеют общего делителя (четвёрка тогда называется примитивной) тогда и только тогда, когда они имеют вид $(x^{3};x^{2}y;xy^{2};y^{3})$где $x,y$ являются взаимно простыми положительными целыми числами .

Дальнейшие замечания

Два четырехугольника 7-Con.

Определение почти конгруэнтных треугольников дает бинарное отношение на множестве треугольников. Это отношение явно не рефлексивно , но оно симметрично . Он не транзитивен : в качестве контрпримера рассмотрим три треугольника с длинами сторон (8;12;18), (12;18;27) и (18;27;40,5).

Существуют бесконечные последовательности треугольников, в которых любые два последующих члена являются треугольниками с 5 Con. Такую последовательность легко построить из любого треугольника, поддерживающего 5-Con: чтобы получить восходящую (соответственно нисходящую) последовательность, сохраните две наибольшие (соответственно наименьшие) стороны и просто выберите третью, большую (соответственно меньшую) сторону. длину, чтобы получить подобный треугольник. Можно легко расположить треугольники в последовательности аккуратным образом, например, по спирали.

Одно из обобщений рассматривает четырехугольники 7-Con , то есть неконгруэнтные (и не обязательно подобные) четырехугольники, у которых четыре угла и три стороны совпадают, или, в более общем смысле, (2n-1)-Con n-угольники.