Распад частиц

В физике элементарных частиц распад частиц — это спонтанный процесс превращения одной нестабильной субатомной частицы во множество других частиц. Каждая из частиц, созданных в этом процессе ( конечное состояние ), должна быть менее массивной, чем исходная, хотя общая масса системы должна сохраняться. Частица нестабильна, если существует хотя бы одно разрешенное конечное состояние, в которое она может распадаться. Нестабильные частицы часто имеют несколько способов распада, каждый из которых имеет свою собственную вероятность . Распады опосредуются одной или несколькими фундаментальными силами . Частицы в конечном состоянии сами могут быть нестабильными и подвержены дальнейшему распаду.

Этот термин обычно отличается от радиоактивного распада , при котором нестабильное атомное ядро ​​превращается в более легкое ядро, сопровождающееся испусканием частиц или радиацией , хотя оба концептуально схожи и часто описываются с использованием одной и той же терминологии.

Вероятность выживания и время жизни частиц

Распад частицы — это процесс Пуассона , и, следовательно, вероятность того, что частица выживет в течение времени t перед распадом ( функция выживания ), определяется экспоненциальным распределением , постоянная времени которого зависит от скорости частицы:

$P(t)=\exp \left(-{\frac {t}{\gamma \tau }}\right)$

где

$\tau$ - среднее время жизни частицы (в состоянии покоя), а

$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$ – Лоренц-фактор частицы.

некоторых элементарных и сложных

Все данные взяты из Particle Data Group .

Тип	Имя	Символ	Масса ( МэВ )	Средний срок службы
Лептон	Электрон / Позитрон	$\mathrm {e} ^{-}\,/\,\mathrm {e} ^{+}$	000 0.511	$>6.6\times 10^{28}\ \mathrm {years} \,$
	Мюон / Антимюон	$\mathrm {\mu } ^{-}\,/\,\mathrm {\mu } ^{+}$	00 105.7 00	$2.2\times 10^{-6}\ \mathrm {seconds} \,$
	Тау лептон / Антитау	$\mathrm {\tau } ^{-}\,/\,\mathrm {\tau } ^{+}$	0 1777 .000	$2.9\times 10^{-13}\ \mathrm {seconds} \,$
Мезон	Нейтральный пион	$\mathrm {\pi } ^{0}\,$	00 135 .000	$8.4\times 10^{-17}\ \mathrm {seconds} \,$
	Заряженный пион	$\mathrm {\pi } ^{+}\,/\,\mathrm {\pi } ^{-}$	00 139.6 00	$2.6\times 10^{-8}\ \mathrm {seconds} \,$
Барион	Протон / Антипротон	$\mathrm {p} ^{+}\,/\,\mathrm {p} ^{-}$	00 938.2 00	$>1.67\times 10^{34}\ \mathrm {years} \,$
	Нейтрон / Антинейтрон	$\mathrm {n} \,/\,\mathrm {\bar {n}}$	00 939.6 00	$885.7\ \mathrm {seconds} \,$
Бозон	W-бозон	$\mathrm {W} ^{+}\,/\,\mathrm {W} ^{-}$	80400 .000	$10^{-25}\ \mathrm {seconds} \,$
	Z-бозон	$\mathrm {Z} ^{0}\,$	91000 .000	$10^{-25}\ \mathrm {seconds} \,$

Скорость распада

В этом разделе используются натуральные единицы , где $c=\hbar =1.\,$

Время жизни частицы определяется обратной скоростью ее распада: $\Gamma$, вероятность в единицу времени распада частицы. Для частицы массы M и четырехимпульса P, распадающейся на частицы с импульсами $p_{i}$, скорость дифференциального распада определяется общей формулой (выражающей золотое правило Ферми )

$d\Gamma _{n}={\frac {S\left|{\mathcal {M}}\right|^{2}}{2M}}d\Phi _{n}(P;p_{1},p_{2},\dots ,p_{n})\,$

где

n — количество частиц, созданных при распаде оригинала,

S — комбинаторный фактор, учитывающий неразличимые конечные состояния (см. ниже),

${\mathcal {M}}\,$ — инвариантный матричный элемент или амплитуда, соединяющая начальное состояние с конечным состоянием (обычно рассчитывается с помощью диаграмм Фейнмана ),

$d\Phi _{n}\,$ является элементом фазового пространства , а

$p_{i}\,$ — четырехимпульс частицы i .

Коэффициент S определяется выражением

$S=\prod _{j=1}^{m}{\frac {1}{k_{j}!}}\,$

где

m — количество наборов неразличимых частиц в конечном состоянии,

$k_{j}\,$ — число частиц типа j , так что $\sum _{j=1}^{m}k_{j}=n\,$.

Фазовое пространство можно определить по формуле

$d\Phi _{n}(P;p_{1},p_{2},\dots ,p_{n})=(2\pi )^{4}\delta ^{4}\left(P-\sum _{i=1}^{n}p_{i}\right)\prod _{i=1}^{n}{\frac {d^{3}{\vec {p}}_{i}}{2(2\pi )^{3}E_{i}}}$

где

$\delta ^{4}\,$ — четырехмерная дельта-функция Дирака ,

${\vec {p}}_{i}\,$ — (трех)импульс частицы i , а

$E_{i}\,$ — энергия частицы i .

Можно интегрировать по фазовому пространству, чтобы получить общую скорость распада для заданного конечного состояния.

Если частица имеет несколько ветвей или мод распада с разными конечными состояниями, ее полная скорость распада получается путем суммирования скоростей распада для всех ветвей. Коэффициент ветвления для каждой моды определяется скоростью ее затухания, деленной на полную скорость затухания.

Двухчастичный распад

В этом разделе используются натуральные единицы , где $c=\hbar =1.\,$

В системе «Центр импульса» распад частицы на две частицы одинаковой массы приводит к их вылету под углом 180° между ними.

...в то время как в лабораторной системе координат родительская частица, вероятно, движется со скоростью, близкой к скорости света, поэтому две испускаемые частицы будут выходить под углами, отличными от углов в центре импульсной системы координат.

Скорость распада

Скажем, родительская частица массы M распадается на две частицы, обозначенные 1 и 2 . В системе покоя родительской частицы

$|{\vec {p}}_{1}|=|{\vec {p}}_{2}|={\frac {[(M^{2}-(m_{1}+m_{2})^{2})(M^{2}-(m_{1}-m_{2})^{2})]^{1/2}}{2M}},\,$

который получается требованием сохранения четырехимпульса при распаде, т.е.

$(M,{\vec {0}})=(E_{1},{\vec {p}}_{1})+(E_{2},{\vec {p}}_{2}).\,$

Кроме того, в сферических координатах

$d^{3}{\vec {p}}=|{\vec {p}}\,|^{2}\,d|{\vec {p}}\,|\,d\phi \,d\left(\cos \theta \right).\,$

Использование дельта-функции для выполнения $d^{3}{\vec {p}}_{2}$ и $d|{\vec {p}}_{1}|\,$ интегралов в фазовом пространстве для конечного состояния двух тел, можно обнаружить, что скорость распада в системе покоя родительской частицы равна

$d\Gamma ={\frac {\left|{\mathcal {M}}\right|^{2}}{32\pi ^{2}}}{\frac {|{\vec {p}}_{1}|}{M^{2}}}\,d\phi _{1}\,d\left(\cos \theta _{1}\right).\,$

Из двух разных кадров

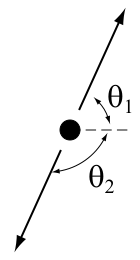
Угол вылета частицы в лабораторной системе координат связан с углом, который она испустила в центре системы импульса, уравнением

$\tan {\theta '}={\frac {\sin {\theta }}{\gamma \left(\beta /\beta '+\cos {\theta }\right)}}$

масса и

Дополнительная информация: Резонанс § Атомный, частиц и молекулярный резонанс ; и резонанс (физика элементарных частиц)

В этом разделе используются натуральные единицы , где $c=\hbar =1.\,$

Масса нестабильной частицы формально представляет собой комплексное число , где действительная часть — это ее масса в обычном понимании, а мнимая часть — скорость ее распада в натуральных единицах . Когда мнимая часть больше реальной части, о частице обычно думают скорее как о резонансе , чем о частице. Это связано с тем, что в квантовой теории поля частица массы M ( действительное число ) часто обменивается между двумя другими частицами, когда для ее создания недостаточно энергии, если время путешествия между этими другими частицами достаточно короткое, порядка 1. /M, согласно принципу неопределенности . Для частицы массы $\scriptstyle M+i\Gamma$, частица может путешествовать за время 1/M, но распадается за время порядка $\scriptstyle 1/\Gamma$. Если $\scriptstyle \Gamma >M$ тогда частица обычно распадается, не успев завершить свой путь.

См. также

• Релятивистское распределение Брейта-Вигнера
• Физика элементарных частиц
• Излучение частиц
• Список частиц
• Слабое взаимодействие

Внешние ссылки

• Джей Ди Джексон (2004). «Кинематика» (PDF) . Группа данных о частицах . Архивировано из оригинала (PDF) 21 ноября 2014 г. Проверено 26 ноября 2006 г. (См. стр. 2).
• Группа данных о частицах .
• « Приключение частиц » Группа данных о частицах , Национальная лаборатория Лоуренса Беркли.