Многогранник Уотермана

В геометрии многогранники Уотермана — это семейство многогранников, открытое около 1990 года математиком Стивом Уотерманом . Многогранник Уотермана создается путем упаковки сфер в соответствии с кубической закрытой (ст) упаковкой (CCP), также известной как гранецентрированная кубическая (ГЦК) упаковка, с последующим сметанием сфер, которые находятся дальше от центра, чем определенный радиус. ^[1] затем создаем выпуклую оболочку центров сфер.

Кубические Close(st) Упакованные сферы радиусом √ 24
Соответствующий многогранник Ватермана W24 Начало 1

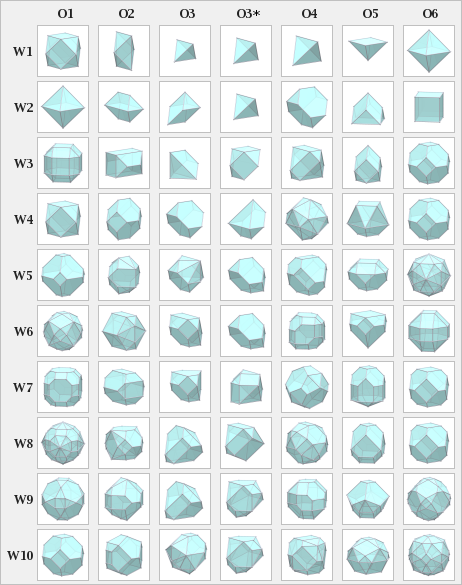
Многогранники Уотермана образуют обширное семейство многогранников. Некоторые из них обладают рядом приятных свойств, таких как множественная симметрия или интересные и правильные формы. Другие представляют собой просто набор граней, образованных из неправильных выпуклых многоугольников .

Наиболее популярные многогранники Уотермана — это многогранники с центрами в точке (0,0,0) и построенные из сотен многоугольников. Такие многогранники напоминают сферы. Фактически, чем больше граней имеет многогранник Уотермана, тем больше он напоминает описанную ему сферу по объему и общей площади.

Каждой точке трехмерного пространства можно сопоставить семейство многогранников Ватермана с разными значениями радиусов описанных сфер. Следовательно, с математической точки зрения мы можем рассматривать многогранники Уотермана как 4D-пространства W(x, y, z, r), где x, y, z — координаты точки в 3D, а r — положительное число, большее 1. . ^[2]

Семь истоков кубической плотной упаковки (ККТ)

В CCP может быть определено семь источников: ^[3] где n = {1, 2, 3, …}:

Начало координат 1: смещение 0,0,0, радиус ${\sqrt {2n}}$
Начало координат 2: смещение ⁠ 1 / 2 ⁠ , ⁠ 1 / 2 ⁠ ,0, радиус ${\tfrac {1}{2}}{\sqrt {2+4n}}$
Начало координат 3: смещение ⁠ 1 / 3 ⁠ , ⁠ 1 / 3 ⁠ , ⁠ 2 / 3 ⁠ , радиус ${\tfrac {1}{3}}{\sqrt {6(n+1)}}$
Начало координат 3*: смещение ⁠ 1 / 3 ⁠ , ⁠ 1 / 3 ⁠ , ⁠ 1 / 3 ⁠ , радиус ${\tfrac {1}{3}}{\sqrt {3+6n}}$
Происхождение 4: смещение ⁠ 1 / 2 ⁠ , ⁠ 1 / 2 ⁠ , ⁠ 1 / 2 ⁠ , радиус ${\tfrac {1}{2}}{\sqrt {3+8(n-1)}}$
Начало координат 5: смещение 0,0, ⁠ 1 / 2 ⁠ , радиус ${\tfrac {1}{2}}{\sqrt {1+4n}}$
Начало координат 6: смещение 1,0,0, радиус ${\sqrt {1+2(n-1)}}$

В зависимости от происхождения выметания получается разная форма и результирующий многогранник.

Связь с Платоновыми и Архимедовыми телами

Некоторые многогранники Уотермана создают Платоновы тела и Архимедовы тела . Для этого сравнения многогранников Ватермана они нормализуются, например, W2 O1 имеет другой размер или объем, чем W1 O6, но имеет ту же форму, что и октаэдр. ^{[ нужна ссылка ]}

Платоновые тела

Тетраэдр: W1 O3*, W2 O3*, W1 O3, W1 O4
Октаэдр: W2 O1, W1 O6
Куб: W2 O6
Икосаэдр и додекаэдр не имеют представления в виде многогранников Уотермана. ^{[ нужна ссылка ]}

Архимедовы тела

Кубооктаэдр : W1 O1, W4 O1
Усеченный октаэдр : W10 O1
Усеченный тетраэдр : W4 O3, W2 O4.
Остальные архимедовы тела не имеют представления в виде многогранников Ватермана. ^{[ нужна ссылка ]}

W7 O1 можно принять за усеченный кубооктаэдр , а W3 O1 = W12 O1 ошибочно принять за ромбокубооктаэдр , но эти многогранники Уотермана имеют две длины ребер и поэтому не могут считаться архимедовыми телами. ^{[ нужна ссылка ]}

Обобщенные многогранники Уотермана

Обобщенные многогранники Уотермана определяются как выпуклая оболочка, полученная из множества точек любого сферического извлечения из регулярной решетки. ^{[ нужна ссылка ]}

Включен подробный анализ следующих 10 решеток – ОЦК, кубооктаэдра, ромба, ГЦК, ГПУ, усеченного октаэдра, ромбдодекаэдра , простой кубической, усеченного тет-тет, усеченного тет, усеченного октаэдра, кубооктаэдра. ^{[ нужна ссылка ]}

Каждая из 10 решеток была исследована, чтобы выделить те конкретные исходные точки, которые представляли собой уникальный многогранник, а также обладали некоторыми минимальными требованиями симметрии. ^{[ нужна ссылка ]} Из жизнеспособной исходной точки внутри решетки существует неограниченное количество многогранников. ^{[ нужна ссылка ]} существует взаимно однозначное соответствие . Учитывая правильный интервал развертки, между каждым целочисленным значением и обобщенным многогранником Уотермана ^{[ нужна ссылка ]}

Примечания

^ Попко, Эдвард С. (2012). Разделенные сферы: геодезика и упорядоченное деление сферы . ЦРК Пресс. стр. 174–177. ISBN 9781466504295 .
^ Визуализация многогранников Уотермана с помощью MuPAD М. Маевского
^ 7 Происхождение многогранников CCP Waterman Марка Ньюболда

Внешние ссылки

[Popko2012-1] Попко, Эдвард С. (2012). Разделенные сферы: геодезика и упорядоченное деление сферы . ЦРК Пресс. стр. 174–177. ISBN 9781466504295 .

[2] Визуализация многогранников Уотермана с помощью MuPAD М. Маевского

[3] 7 Происхождение многогранников CCP Waterman Марка Ньюболда

[1]

[2]

[3]