Уравнение Селлмейера

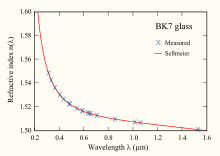
То же, что и график выше, но для сравнения используется уравнение Коши (синяя линия). Хотя уравнение Коши (синяя линия) значительно отклоняется от измеренных показателей преломления за пределами видимой области (которая заштрихована красным), уравнение Селлмейера (зеленая пунктирная линия) этого не делает.

Уравнение Селлмейера представляет собой эмпирическую зависимость между показателем преломления и длиной волны для конкретной прозрачной среды . Уравнение используется для определения дисперсии света . в среде

Впервые оно было предложено в 1872 году Вольфгангом Селлмайером и представляло собой развитие работы Огюстена Коши по уравнению Коши для моделирования дисперсии. ^[1]

Уравнение

В своей исходной и наиболее общей форме уравнение Селлмейера имеет вид

n^{2}(\lambda )=1+\sum _{i}{\frac {B_{i}\lambda ^{2}}{\lambda ^{2}-C_{i}}}

,

где n — показатель преломления, λ — длина волны, а B _i и C _i — экспериментально определенные Селлмейера коэффициенты . Эти коэффициенты обычно указываются для λ в микрометрах . Обратите внимание, что эта λ — это длина волны в вакууме, а не в самом материале, которая равна λ/n. , иногда используется другая форма уравнения Для некоторых типов материалов, например кристаллов .

Каждый член суммы представляет собой резонанс поглощения силы B _i на длине волны $\sqrt C i$ . Например, приведенные ниже коэффициенты для BK7 соответствуют двум резонансам поглощения в ультрафиолетовом диапазоне и одному в среднем инфракрасном диапазоне. Аналитически этот процесс основан на аппроксимации основных оптических резонансов дельта-функциями Дирака с последующим применением соотношений Крамерса-Кронига . В результате действительная и мнимая части показателя преломления становятся физически ощутимыми. ^[2] Однако вблизи каждого пика поглощения уравнение дает нефизические значения n ² более точную модель дисперсии, такую как модель Гельмгольца = ±∞, и в этих диапазонах длин волн необходимо использовать .

Если все члены указаны для материала, то на длинных волнах вдали от пиков поглощения значение n стремится к

{\begin{matrix}n\approx {\sqrt {1+\sum _{i}B_{i}}}\approx {\sqrt {\varepsilon _{r}}}\end{matrix}},

где ε _r — относительная диэлектрическая проницаемость среды.

Для характеристики стекол обычно используют уравнение, состоящее из трех членов: ^[3]^[4]

n^{2}(\lambda )=1+{\frac {B_{1}\lambda ^{2}}{\lambda ^{2}-C_{1}}}+{\frac {B_{2}\lambda ^{2}}{\lambda ^{2}-C_{2}}}+{\frac {B_{3}\lambda ^{2}}{\lambda ^{2}-C_{3}}},

коэффициенты для обычного боросиликатного кронного стекла , известного как BK7 В качестве примера ниже показаны :

Коэффициент	Ценить
Б ₁	1.03961212
B_Б2	0.231792344
B_Б3	1.01046945
С ₁	6.00069867×10 ⁻³ мкм ²
С ₂	2.00179144×10 ⁻² мкм ²
С ₃	1.03560653×10 ² мкм ²

Для обычных оптических стекол показатель преломления, рассчитанный с помощью трехчленного уравнения Селлмейера, отклоняется от фактического показателя преломления менее чем на 5 × 10. ⁻⁶ в диапазоне длин волн ^[5] от 365 нм до 2,3 мкм, что порядка однородности образца стекла. ^[6] Иногда добавляются дополнительные термины, чтобы сделать расчет еще более точным.

Иногда уравнение Селлмейера используется в двухчленной форме: ^[7]

n^{2}(\lambda )=A+{\frac {B_{1}\lambda ^{2}}{\lambda ^{2}-C_{1}}}+{\frac {B_{2}\lambda ^{2}}{\lambda ^{2}-C_{2}}}.

Здесь коэффициент A представляет собой аппроксимацию вклада коротковолнового поглощения (например, ультрафиолетового) в показатель преломления на более длинных волнах. Существуют и другие варианты уравнения Селлмейера, которые могут учитывать изменение показателя преломления материала из-за температуры , давления и других параметров.

Вывод

Аналитически уравнение Селлмейера моделирует показатель преломления как результат серии оптических резонансов внутри объемного материала. Его вывод из соотношений Крамерса-Кронига требует нескольких предположений о материале, любые отклонения от которых повлияют на точность модели:

Существует несколько резонансов, и окончательный показатель преломления можно рассчитать как сумму вкладов всех резонансов.
Все оптические резонансы находятся на длинах волн, далеких от интересующих длин волн, к которым применяется модель.
На этих резонансных частотах мнимая составляющая восприимчивости ( ${\chi _{i}}$ ) можно смоделировать как дельта-функцию .

Из последнего пункта комплексный показатель преломления (и электрическая восприимчивость ) становится:

\chi _{i}(\omega )=\sum _{i}A_{i}\delta (\omega -\omega _{i})

Действительная часть показателя преломления получается в результате применения соотношений Крамерса-Кронига к мнимой части:

n^{2}=1+\chi _{r}(\omega )=1+{\frac {2}{\pi }}\int _{0}^{\infty }{\frac {\omega \chi _{i}(\omega )}{\omega ^{2}-\Omega ^{2}}}d\omega

Подставляя первое уравнение выше для мнимой составляющей:

n^{2}=1+{\frac {2}{\pi }}\int _{0}^{\infty }\sum _{i}A_{i}\delta (\omega -\omega _{i}){\frac {\omega }{\omega ^{2}-\Omega ^{2}}}d\omega

Порядок суммирования и интегрирования можно менять местами. При оценке это дает следующее, где $H$ это функция Хевисайда :

n^{2}=1+{\frac {2}{\pi }}\sum _{i}A_{i}\int _{0}^{\infty }\delta (\omega -\omega _{i}){\frac {\omega }{\omega ^{2}-\Omega ^{2}}}d\omega =1+{\frac {2}{\pi }}\sum _{i}A_{i}{\frac {\omega _{i}H(\omega _{i})}{\omega _{i}^{2}-\Omega ^{2}}}

Поскольку предполагается, что область находится вдали от каких-либо резонансов (предположение 2 выше), $H(\omega _{i})$ оценивается как 1, и получается знакомая форма уравнения Селлмейера:

n^{2}=1+{\frac {2}{\pi }}\sum _{i}A_{i}{\frac {\omega _{i}}{\omega _{i}^{2}-\Omega ^{2}}}

Переставив члены, константы $B_{i}$ и $C_{i}$ можно подставить в приведенное выше уравнение, чтобы получить уравнение Селлмейера. ^[2]

Коэффициенты

Таблица коэффициентов уравнения Зеллмейера ^[8]
Материал	Б ₁	B_Б2	B_Б3	С ₁ , мкм ²	С ₂ , мкм ²	С ₃ , мкм ²
боросиликатное кроновое стекло (известный как BK7 )	1.03961212	0.231792344	1.01046945	6.00069867×10 ⁻³	2.00179144×10 ⁻²	103.560653
сапфир (для обычной волны )	1.43134930	0.65054713	5.3414021	5.2799261×10 ⁻³	1.42382647×10 ⁻²	325.017834
сапфир (для необыкновенной волны )	1.5039759	0.55069141	6.5927379	5.48041129×10 ⁻³	1.47994281×10 ⁻²	402.89514
плавленый кварц	0.696166300	0.407942600	0.897479400	4.67914826×10 ⁻³	1.35120631×10 ⁻²	97.9340025
Фторид магния	0.48755108	0.39875031	2.3120353	0.001882178	0.008951888	566.13559

См. также

Уравнение Коши

Ссылки

^ Селлмейер, В. (1872). «О резонансах частиц тела, возбуждаемых эфирными колебаниями, и их реакции на первые, особенно для объяснения рассеяния и его аномалий (Часть II)» . Анналы физики и химии . 223 (11): 386–403. дои : 10.1002/andp.18722231105 .
^ Перейти обратно: ^а ^б «2.7: Отношения Крамерса-Крёнига» . Инженерные библиотеки LibreTexts . 06.04.2021 . Проверено 9 июля 2024 г.
^ Показатель преломления и дисперсия . Технический информационный документ Schott TIE-29 (2007 г.).
^ Пашотта, доктор Рюдигер. «Энциклопедия лазерной физики и техники — формула Селлмейера, показатель преломления, уравнение Селлмейера, дисперсионная формула» . www.rp-photonics.com . Проверено 14 сентября 2018 г.
^ «Оптические свойства» .
^ «Гарантия качества» .
^ Гош, Горачанд (1997). «Коэффициенты Селлмейера и дисперсия термооптических коэффициентов для некоторых оптических стекол» . Прикладная оптика . 36 (7): 1540–6. Бибкод : 1997ApOpt..36.1540G . дои : 10.1364/AO.36.001540 . ПМИД 18250832 .
^ «Архивная копия» . Архивировано из оригинала 11 октября 2015 г. Проверено 16 января 2015 г. {{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )

Внутренние ссылки

RefractiveIndex.INFO База данных показателей преломления, содержащая коэффициенты Селлмейера для многих сотен материалов.
Браузерный калькулятор, рассчитывающий показатель преломления на основе коэффициентов Селлмейера.
Annalen der Physik - свободный доступ, оцифровано Национальной библиотекой Франции.
Коэффициенты Селлмейера для 356 стаканов от Охара, Хойя и Шотт

[1] Селлмейер, В. (1872). «О резонансах частиц тела, возбуждаемых эфирными колебаниями, и их реакции на первые, особенно для объяснения рассеяния и его аномалий (Часть II)» . Анналы физики и химии . 223 (11): 386–403. дои : 10.1002/andp.18722231105 .

[b841-2] Перейти обратно: ^а ^б «2.7: Отношения Крамерса-Крёнига» . Инженерные библиотеки LibreTexts . 06.04.2021 . Проверено 9 июля 2024 г.

[3] Показатель преломления и дисперсия . Технический информационный документ Schott TIE-29 (2007 г.).

[4] Пашотта, доктор Рюдигер. «Энциклопедия лазерной физики и техники — формула Селлмейера, показатель преломления, уравнение Селлмейера, дисперсионная формула» . www.rp-photonics.com . Проверено 14 сентября 2018 г.

[5] «Оптические свойства» .

[6] «Гарантия качества» .

[7] Гош, Горачанд (1997). «Коэффициенты Селлмейера и дисперсия термооптических коэффициентов для некоторых оптических стекол» . Прикладная оптика . 36 (7): 1540–6. Бибкод : 1997ApOpt..36.1540G . дои : 10.1364/AO.36.001540 . ПМИД 18250832 .

[8] «Архивная копия» . Архивировано из оригинала 11 октября 2015 г. Проверено 16 января 2015 г. {{cite web}}: CS1 maint: архивная копия в заголовке ( ссылка )

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]