Граф Фолкмана

Граф Фолкмана
Граф Фолкмана
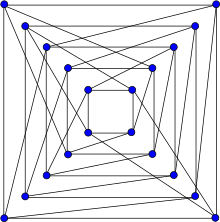	Рисунок по Фолкману (1967) , рисунок 1.
Назван в честь	Джон Фолкман
Вершины	20
Края	40
Радиус	3
Диаметр	4
Обхват	4
Автоморфизмы	5! · 2 5 = 3840
Хроматическое число	2
Хроматический индекс	4
Род	3
Толщина книги	3
Номер очереди	2
Характеристики	двусторонний ; Эйлеров ; гамильтониан ; Обычный ; Полусимметричный ;
	Таблица графиков и параметров

В математической области теории графов граф Фолкмана представляет собой 4- регулярный граф с 20 вершинами и 40 ребрами. Это правильный двудольный граф, симметрия которого переносит каждое ребро в каждое другое ребро, но две стороны его двудольного графа не симметричны друг другу, что делает его наименьшим из возможных полусимметричных графов . ^[1] Он назван в честь Джона Фолкмана , который построил его для этого объекта в 1967 году. ^[2]

Граф Фолкмана может быть построен либо с использованием модульной арифметики , либо как разделенный дубль полного пятивершинного графа . Помимо исследования его симметрии, он также исследовался как контрпример для некоторых вопросов встраивания графов .

Строительство

Полусимметричные графы определяются как регулярные графы (то есть графы, в которых все вершины касаются одинакового количества ребер), в которых каждые два ребра симметричны друг другу, но некоторые две вершины не симметричны. Джон Фолкман был вдохновлен на определение и исследование этих графиков в статье 1967 года после просмотра неопубликованной рукописи Э. Даубера и Фрэнка Харари , в которой были приведены примеры графов, удовлетворяющих условию симметрии, но не условию регулярности. Исходная конструкция этого графа Фолкмана была частным случаем более общей конструкции полусимметричных графов с использованием модульной арифметики , основанной на простом числе. $p$ конгруэнтно 1 по модулю 4. Для каждого такого простого числа существует число $r$ такой, что $r^{2}=-1$ против $p$ , а Фолкман использует модульную арифметику для построения полусимметричного графа с $2pr$ вершины. Граф Фолкмана является результатом этой конструкции для $p=5$ и $r=2$ . ^[2]

Другая конструкция графа Фолкмана начинается с полного графа с пятью вершинами: $K_{5}$ . На каждое из десяти ребер помещается новая вершина. $K_{5}$ , разделяя каждое ребро на путь с двумя ребрами. Тогда каждая из пяти исходных вершин $K_{5}$ удваивается, заменяя его двумя вершинами с теми же соседями. Десять вершин подразделения образуют одну сторону двудольного графа Фолкмана, а десять вершин в парах-близнецах исходят из удвоенных вершин графа Фолкмана. $K_{5}$ образуют другую сторону бираздела. ^[3]^[4]

Поскольку каждое ребро результата получается из удвоенной половины ребра $K_{5}$ , и потому что $K_{5}$ имеет симметрии, переводящие каждое полуребро в любое другое полуребро, результат является транзитивным по ребру. Он не является вершинно-транзитивным, поскольку вершины подразделения не являются близнецами ни одной другой вершины, что отличает их от удвоенных вершин, происходящих из $K_{5}$ . ^[3] Любой 4-регулярный полусимметричный граф, в котором некоторые две вершины имеют одну и ту же окрестность, можно построить таким же образом, разделив и затем удвоив 4-регулярный симметричный граф, такой как $K_{5}$ или график октаэдра . Однако существуют и более крупные 4-регулярные полусимметричные графы, не имеющие вершин-близнецов. ^[4]^[5]

Алгебраические свойства

Группа автоморфизмов графа Фолкмана (его группа симметрий) объединяет $5!$ симметрии $K_{5}$ с $2^{5}$ способы замены некоторых пар удвоенных вершин, всего $5!\cdot 2^{5}=3840$ симметрии. Эта группа действует транзитивно на ребрах графа Фолкмана (она включает симметрию, переводящую любое ребро в любое другое ребро), но не на его вершинах. Граф Фолкмана — это наименьший неориентированный граф, который является реберно-транзитивным и регулярным, но не вершинно-транзитивным . ^[6] Такие графы называются полусимметричными и впервые были изучены Фолкманом в 1967 году, который открыл граф с 20 вершинами, который теперь назван в его честь. ^[2]

Как и все полусимметричные графы, граф Фолкмана двудольный . Его группа автоморфизмов включает в себя симметрии, переводящие любую вершину в любую другую вершину, находящуюся на той же стороне двураздела, но не переводящие вершину на другую сторону двураздела. Хотя можно прямо утверждать, что граф Фолкмана не является вершинно-транзитивным, это также можно объяснить теоретико-групповым образом: его симметрии примитивно действуют на вершины, построенные как точки подразделения $K_{5}$ , но примитивно на вершинах, построенных удвоением вершин $K_{5}$ . Каждая симметрия отображает удвоенную пару вершин в другую удвоенную пару вершин, но не существует группировки вершин подразделения, которая сохраняется симметриями. ^[7]

Характеристический полином графа Фолкмана равен $(x-4)x^{10}(x+4)(x^{2}-6)^{4}$ . ^[8]

Другие объекты недвижимости

Граф Фолкмана имеет гамильтонов цикл и, более строго, гамильтоново разложение на два гамильтоновых цикла. Как и у любого двудольного графа, его хроматическое число равно двум, а его хроматический индекс (минимальное количество цветов, необходимое для раскраски его ребер так, чтобы никакие два ребра одного цвета не пересекались в вершине) равен его максимальной степени. ^[9] что в данном случае четыре. Например, такую раскраску можно получить, используя поочередно два цвета для каждого цикла гамильтонова разложения.

Его радиус равен 3, а диаметр равен 4. Если $v$ является одной из удвоенных вершин $K_{5}$ построения, то все остальные вершины находятся не более чем в трех шагах от $v$ . Однако из конструкции присутствуют пары вершин подразделения (исходящие из непересекающихся ребер $K_{5}$ ), которые находятся на расстоянии четырех шагов друг от друга. Поскольку граф содержит много 4-циклов, его обхват равен 4 — минимально возможному для двудольного графа. Он также 4- вершинно-связен и 4- реберно-связен . Его ширина дерева и ширина клики равны 5. ^[10]

Граф Фолкмана имеет род 3: его можно вложить в тройной тор , но не в любую более простую ориентированную поверхность. ^[11]^[12] Он имеет толщину книги 3, но требует пяти страниц для «диспергируемого» вложения книги, в котором каждая страница представляет собой совпадение , что опровергает гипотезу Фрэнка Бернхарта и Пола Кайнена о том, что для дисперсионного книжного вложения регулярных графов требуется только количество страниц, равное их числу. степень. ^[3]

Ссылки

^ Бош, Ф.; Тинделл, Р. (1984), «Циркулянты и их связности», Журнал теории графов , 8 (4): 487–499, doi : 10.1002/jgt.3190080406 , MR 0766498
^ Jump up to: ^а ^б ^с Фолкман, Дж. (1967), «Регулярные линейно-симметричные графы», Журнал комбинаторной теории , 3 (3): 215–232, doi : 10.1016/S0021-9800(67)80069-3
^ Jump up to: ^а ^б ^с Алам, Джавахерул, Мэриленд; Бекос, Майкл А.; Дуймович, Вида ; Гронеманн, Мартин; Кауфманн, Майкл; Пупырев, Сергей (2021), «О диспергируемых книжных вложениях», Theoretical Computer Science , 861 : 1–22, arXiv : 1803.10030 , doi : 10.1016/j.tcs.2021.01.035 , MR 4221556
^ Jump up to: ^а ^б Поточник, Примож; Уилсон, Стивен Э. (2014), «Структуры связывающих колец и четырехвалентные полусимметричные графы», Ars Mathematica Contemporanea , 7 (2): 341–352, doi : 10.26493/1855-3974.311.4a8 , MR 3240442
^ Поточник, Примож; Уилсон, Стив (2007), «Тетравалентные реберно-транзитивные графы с обхватом не более 4», Журнал комбинаторной теории , серия B, 97 (2): 217–236, doi : 10.1016/j.jctb.2006.03.007 , MR 2290322
^ Скиена, Стивен (1990), Реализация дискретной математики: комбинаторика и теория графов с Mathematica , Ридинг, Массачусетс: Аддисон-Уэсли, стр. 186–187.
^ Зив-Ав, Матан (2013), Взаимодействие между когерентными конфигурациями и некоторыми классами объектов в экстремальной комбинаторике (PDF) (докторская диссертация), Университет Бен-Гуриона, стр. 24–25
^ Вайсштейн, Эрик В. , «График Фолкмана» , MathWorld
^ Гэлвин, Фред (1995), «Список хроматических индексов двудольного мультиграфа», Журнал комбинаторной теории , серия B, 63 (1): 153–158, doi : 10.1006/jctb.1995.1011 , MR 1309363
^ Хойле, Марин; Зайдер, Стефан (2015), «Подход SAT к ширине клики», ACM Transactions on Computational Logic , 16 (3): 24:1–24:27, arXiv : 1304.5498 , doi : 10.1145/2736696
^ Кондер, Марстон ; Стоукс, Клара (2019), «Новые методы поиска вложений минимальных родов графов на ориентируемых и неориентируемых поверхностях» , Ars Mathematica Contemporanea , 17 (1): 1–35, doi : 10.26493/1855-3974.1800.40c , hdl : 2292/57926 , МР 3992757
^ Бринкманн, Гуннар (2022), «Практический алгоритм вычисления рода» , Ars Mathematica Contemporanea , 22 (4), статья № 1, arXiv : 2005.08243 , doi : 10.26493/1855-3974.2320.c2d , MR 4498572 , S2CID 218674244

[bt84-1] Бош, Ф.; Тинделл, Р. (1984), «Циркулянты и их связности», Журнал теории графов , 8 (4): 487–499, doi : 10.1002/jgt.3190080406 , MR 0766498

[folkman-2] Jump up to: ^а ^б ^с Фолкман, Дж. (1967), «Регулярные линейно-симметричные графы», Журнал комбинаторной теории , 3 (3): 215–232, doi : 10.1016/S0021-9800(67)80069-3

[abdgkp-3] Jump up to: ^а ^б ^с Алам, Джавахерул, Мэриленд; Бекос, Майкл А.; Дуймович, Вида ; Гронеманн, Мартин; Кауфманн, Майкл; Пупырев, Сергей (2021), «О диспергируемых книжных вложениях», Theoretical Computer Science , 861 : 1–22, arXiv : 1803.10030 , doi : 10.1016/j.tcs.2021.01.035 , MR 4221556

[pw14-4] Jump up to: ^а ^б Поточник, Примож; Уилсон, Стивен Э. (2014), «Структуры связывающих колец и четырехвалентные полусимметричные графы», Ars Mathematica Contemporanea , 7 (2): 341–352, doi : 10.26493/1855-3974.311.4a8 , MR 3240442

[pw07-5] Поточник, Примож; Уилсон, Стив (2007), «Тетравалентные реберно-транзитивные графы с обхватом не более 4», Журнал комбинаторной теории , серия B, 97 (2): 217–236, doi : 10.1016/j.jctb.2006.03.007 , MR 2290322

[skiena-6] Скиена, Стивен (1990), Реализация дискретной математики: комбинаторика и теория графов с Mathematica , Ридинг, Массачусетс: Аддисон-Уэсли, стр. 186–187.

[ziv-av-7] Зив-Ав, Матан (2013), Взаимодействие между когерентными конфигурациями и некоторыми классами объектов в экстремальной комбинаторике (PDF) (докторская диссертация), Университет Бен-Гуриона, стр. 24–25

[mathworld-8] Вайсштейн, Эрик В. , «График Фолкмана» , MathWorld

[galvin-9] Гэлвин, Фред (1995), «Список хроматических индексов двудольного мультиграфа», Журнал комбинаторной теории , серия B, 63 (1): 153–158, doi : 10.1006/jctb.1995.1011 , MR 1309363

[hs15-10] Хойле, Марин; Зайдер, Стефан (2015), «Подход SAT к ширине клики», ACM Transactions on Computational Logic , 16 (3): 24:1–24:27, arXiv : 1304.5498 , doi : 10.1145/2736696

[cs19-11] Кондер, Марстон ; Стоукс, Клара (2019), «Новые методы поиска вложений минимальных родов графов на ориентируемых и неориентируемых поверхностях» , Ars Mathematica Contemporanea , 17 (1): 1–35, doi : 10.26493/1855-3974.1800.40c , hdl : 2292/57926 , МР 3992757

[brinkmann-12] Бринкманн, Гуннар (2022), «Практический алгоритм вычисления рода» , Ars Mathematica Contemporanea , 22 (4), статья № 1, arXiv : 2005.08243 , doi : 10.26493/1855-3974.2320.c2d , MR 4498572 , S2CID 218674244

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]