✖


Jump to content

Набор дуг обратной связи

Это хорошая статья. Нажмите здесь для получения дополнительной информации.

Разделение ориентированного графа на минимальный набор дуг обратной связи (красные пунктирные ребра) и максимальный ациклический подграф (синие сплошные ребра)

В теории графов и графовых алгоритмах или набор дуг обратной связи набор ребер обратной связи в ориентированном графе — это подмножество ребер графа, которое содержит хотя бы одно ребро из каждого цикла в графе. Удаление этих ребер из графа нарушает все циклы, создавая ациклический подграф данного графа, часто называемый ориентированным ациклическим графом . Набор дуг обратной связи с наименьшим количеством возможных ребер является минимальным набором дуг обратной связи , и его удаление оставляет максимальный ациклический подграф ; взвешенные версии этих задач оптимизации также используются . Если набор дуг обратной связи минимален, то есть удаление любого ребра из него создает подмножество, которое не является набором дуг обратной связи, то у него есть дополнительное свойство: переворачивание всех его ребер, а не удаление их, создает ориентированный ациклический граф.

Наборы дуг обратной связи применяются в анализе цепей, химической инженерии , тупиковых ситуаций разрешении , рейтинговом голосовании , ранжировании участников спортивных мероприятий, математической психологии , этологии и рисовании графиков . Нахождение минимальных наборов дуг обратной связи и максимальных ациклических подграфов является NP-трудной задачей ; ее можно решить точно за экспоненциальное время или за управляемое время с фиксированными параметрами . За полиномиальное время минимальный набор дуг обратной связи может быть аппроксимирован с точностью до полилогарифмического коэффициента аппроксимации , а максимальные ациклические подграфы могут быть аппроксимированы с точностью до постоянного коэффициента. И то, и другое трудно приблизить ближе, чем какой-то постоянный коэффициент, и этот результат о невозможности аппроксимации можно усилить с помощью гипотезы об уникальных играх . Для турнирных графов минимальный набор дуг обратной связи можно аппроксимировать более точно, а для планарных графов обе задачи можно решить точно за полиномиальное время.

Тесно связанная проблема, набор вершин обратной связи , представляет собой набор вершин, содержащий по крайней мере одну вершину из каждого цикла в ориентированном или неориентированном графе. В неориентированных графах остовные деревья представляют собой самые большие ациклические подграфы, а количество ребер, удаленных при формировании остовного дерева, является рангом схемы .

Приложения [ править ]

Результаты мужского пляжного волейбола на Олимпийских играх 2016 года , группа F, и рейтинг минимального отклонения для этих результатов. Стрелки направлены от проигравшего к победителю каждого матча и окрашены в синий цвет, если результат соответствует рейтингу, и красный в случае неудачи, когда результат не соответствует рейтингу. В таком рейтинге огорчает только один матч, в котором США обыграли QAT. Фактический рейтинг, используемый на Олимпийских играх, отличался тем, что ESP опережал QAT по установленному соотношению, в результате чего их матч был расценен как еще одно разочарование. [1]

Некоторые проблемы, связанные с поиском рейтингов или упорядочений, можно решить, найдя дугу обратной связи, установленную на турнирном графе , ориентированном графе с одним ребром между каждой парой вершин. Перестановка ребер набора дуг обратной связи дает ориентированный ациклический граф , уникальный топологический порядок которого можно использовать в качестве желаемого ранжирования. Приложения этого метода включают следующее:

  • В спортивных соревнованиях с круговой системой результаты каждой игры могут быть записаны путем направления преимущества от проигравшего к победителю каждой игры. Нахождение минимальной дуги обратной связи в полученном графе, изменение ее ребер и топологическое упорядочение дают рейтинг всем конкурентам. Среди всех различных способов выбора рейтинга он сводит к минимуму общее количество неудач, игр, в которых участник с более низким рейтингом побеждает конкурента с более высоким рейтингом. [2] [3] [4] Во многих видах спорта используются более простые методы построения рейтинговых систем групповых турниров, основанные на очках, начисляемых за каждую игру; [5] эти методы могут обеспечить постоянное приближение к рейтингу минимального отклонения. [6]
  • В приматологии в этологии и, в более общем смысле , иерархии доминирования часто определяются путем поиска порядка с наименьшим количеством изменений в наблюдаемом поведении доминирования, что является еще одной формой проблемы множества дуг минимальной обратной связи. [7] [8] [9]
  • В математической психологии представляет интерес определение ранжирования субъектами наборов объектов в соответствии с заданным критерием, например, их предпочтением или восприятием размера, на основе попарных сравнений между всеми парами объектов. Минимальная дуга обратной связи, заданная в турнирном графике, обеспечивает рейтинг, который не согласуется с как можно меньшим количеством парных результатов. [2] [10] В качестве альтернативы, если эти сравнения приводят к независимым вероятностям для каждого парного упорядочения, то оценка максимального правдоподобия общего рейтинга может быть получена путем преобразования этих вероятностей в логарифмические вероятности и нахождения дуги обратной связи с минимальным весом, установленной в результирующем турнире. [2] [3]
  • Тот же самый порядок максимального правдоподобия можно использовать для сериализации , проблемы в статистике и исследовательском анализе данных , заключающейся в упорядочивании элементов в линейном порядке, в тех случаях, когда доступны данные, обеспечивающие попарное сравнение между элементами. [3] [11] [12]
  • При ранжированном голосовании метод Кемени -Янга можно описать как поиск порядка, который минимизирует сумму по парам кандидатов числа избирателей, которые предпочитают противоположный порядок для этой пары. [13] Это можно сформулировать и решить как задачу множества дуг обратной связи с минимальным весом, в которой вершины представляют кандидатов, ребра направлены так, чтобы представлять победителя каждого личного соревнования, а стоимость каждого ребра представляет количество избирателей. кто был бы недоволен, если бы присвоил более высокий рейтинг проигравшему в очном противостоянии. [14]

Еще одно раннее применение наборов дуг обратной связи касалось проектирования последовательных логических схем, в которых сигналы могут циклически распространяться по схеме, а не всегда переходить от входов к выходам. В таких схемах минимальный набор дуг обратной связи характеризует количество точек, в которых необходимо усиление, чтобы сигналы могли распространяться без потери информации. [15] В синхронных схемах, состоящих из асинхронных компонентов, синхронизация может быть достигнута путем размещения тактовых вентилей на краях набора дуг обратной связи. [16] Кроме того, разрезание цепи на наборе дуг обратной связи сводит оставшуюся схему к комбинационной логике , упрощая ее анализ, а размер набора дуг обратной связи определяет, какой объем дополнительного анализа необходим для понимания поведения цепи на разрезе. [15] Аналогичным образом, в схемах технологических химического машиностроения разрыв границ технологической диаграммы на наборе дуг обратной связи и угадывание или проверка всех возможностей значений на этих краях позволяет систематически анализировать остальную часть процесса, поскольку его ацикличность. В этом приложении идея ломать края таким образом называется «разрывом». [17]

При рисовании многослойного графа вершины данного ориентированного графа разбиваются на упорядоченную последовательность подмножеств (слоев рисунка), и каждое подмножество размещается вдоль горизонтальной линии этого рисунка, причем ребра проходят вверх и вниз между ними. слои. В чертежах этого типа желательно, чтобы большинство или все ребра были ориентированы последовательно вниз, а не смешивались с ребрами, направленными вверх и вниз, чтобы отношения достижимости на чертеже были более визуально очевидными. Это достигается путем нахождения минимального или минимального набора дуг обратной связи, изменения ребер в этом наборе местами, а затем выбора разделения на слои таким образом, чтобы это соответствовало топологическому порядку результирующего ациклического графа. [18] [19] Наборы дуг обратной связи также использовались для другой подзадачи рисования многослойных графов - упорядочивания вершин в последовательных парах слоев. [20]

При тупиков разрешении в операционных системах проблема удаления наименьшего числа зависимостей для выхода из тупика может быть смоделирована как задача поиска минимального набора дуг обратной связи. [21] [22] Однако из-за вычислительной сложности поиска этого набора и необходимости обеспечения скорости компонентов операционной системы в этом приложении часто используются эвристики, а не точные алгоритмы. [22]

Алгоритмы [ править ]

Эквиваленты [ править ]

Минимальный набор дуг обратной связи и максимальный ациклический подграф эквивалентны для целей точной оптимизации, поскольку один является дополняющим набором другого. Однако для параметризованной сложности и аппроксимации они различаются, поскольку анализ, используемый для этих типов алгоритмов, зависит от размера решения, а не только от размера входного графа, а минимальный набор дуг обратной связи и максимальный ациклический подграф имеют разные значения. размеры друг от друга. [23]

Набор дуг обратной связи данного графа то же самое, что набор вершин обратной связи ориентированного линейного графа . Здесь набор вершин обратной связи определяется аналогично набору дуг обратной связи как подмножество вершин графа, удаление которых приведет к устранению всех циклов. Линейный график ориентированного графа имеет вершину для каждого ребра и ребро для каждого двуреберного пути в . В другом направлении минимальный набор вершин обратной связи данного графа может быть получено из решения задачи о минимальном наборе дуг обратной связи на графе, полученном путем разделения каждой вершины на две вершины: одну для входящих ребер и одну для исходящих ребер. Эти преобразования позволяют преобразовывать друг в друга точные алгоритмы для наборов дуг обратной связи и наборов вершин обратной связи с соответствующим переводом границ их сложности. Однако это преобразование не сохраняет качество аппроксимации задачи о максимальном ациклическом подграфе. [21] [24]

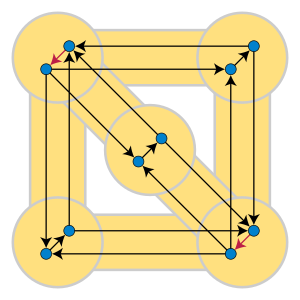
Ориентированный граф с тремя сильно связными компонентами , крайнюю правую из которых можно разбить в вершине сочленения. на две двусвязные компоненты , каждая из которых представляет собой цикл из двух вершин. Проблема набора дуг обратной связи может быть решена отдельно в каждом сильносвязном компоненте и в каждом двусвязном компоненте сильносвязного компонента.

Как при точном, так и при приближенном решении проблемы множества дуг обратной связи достаточно решить отдельно каждый сильно связный компонент данного графа и еще дальше разбить эти сильно связные компоненты на их двусвязные компоненты, разделив их в вершинах сочленения. Выбор решения в рамках любой из этих подзадач не влияет на остальные, а ребра, не входящие ни в одну из этих компонент, бесполезны для включения в множество дуг обратной связи. [25] Когда один из этих компонентов можно разделить на два несвязных подграфа путем удаления двух вершин, применяется более сложная декомпозиция, позволяющая разделить проблему на подзадачи, полученные из трехсвязных компонентов ее сильно связанных компонентов. [26]

Точно [ править ]

Один из способов найти минимальный набор дуг обратной связи - это найти такой порядок вершин, чтобы как можно меньше ребер было направлено от более поздних вершин к более ранним в упорядочении. [27] Поиск перестановок всех -граф вершин займет время , но метод динамического программирования , основанный на алгоритме Хелда – Карпа, позволяет найти оптимальную перестановку за время , также используя экспоненциальное количество пространства. [28] [29] Алгоритм «разделяй и властвуй» , который проверяет все разбиения вершин на два равных подмножества и выполняет рекурсию внутри каждого подмножества, может решить проблему вовремя . , используя полиномиальное пространство . [29]

В параметризованной сложности время работы алгоритмов измеряется не только размером входного графа, но и отдельным параметром графа. В частности, для задачи о минимальном наборе дуг обратной связи так называемым естественным параметром является размер минимального набора дуг обратной связи. На графиках с вершины с натуральным параметром , проблема набора дуг обратной связи может быть решена вовремя , преобразуя ее в эквивалентную задачу набора вершин обратной связи и применяя параметризованный алгоритм набора вершин обратной связи. Поскольку показатель степени в этом алгоритме является константой , независимо от , этот алгоритм называется управляемым с фиксированными параметрами. [30]

Другие параметры, помимо естественного параметра, также были изучены. Управляемый алгоритм с фиксированными параметрами, использующий динамическое программирование, может вовремя найти минимальные наборы дуг обратной связи . , где — ранг схемы базового неориентированного графа. Ранг схемы — это неориентированный аналог множества дуг обратной связи, минимальное количество ребер, которые необходимо удалить из графа, чтобы свести его к остовному дереву ; его гораздо проще вычислить, чем набор минимальных дуг обратной связи. [24] Для графиков ширины дерева Динамическое программирование на древовидной декомпозиции графа может найти минимальную дугу обратной связи, установленную за время, полиномиальное по размеру графа и экспоненциальное по времени. . Согласно гипотезе экспоненциального времени , нет лучшей зависимости от возможно. [31]

Вместо минимизации размера набора дуг обратной связи исследователи также рассмотрели возможность минимизировать максимальное количество ребер, удаленных из любой вершины. Этот вариант задачи может быть решен за линейное время . [32] Все наборы минимальных дуг обратной связи могут быть перечислены с помощью алгоритма с полиномиальной задержкой на набор. [33]

Приблизительно [ править ]

Нерешенная задача по математике :

Имеет ли задача набора дуг обратной связи алгоритм аппроксимации с постоянным коэффициентом аппроксимации?

(еще нерешенные задачи по математике)

Самый известный алгоритм аппроксимации с полиномиальным временем для набора дуг обратной связи имеет непостоянный коэффициент аппроксимации. . Это означает, что размер набора дуг обратной связи, который он обнаруживает, не более чем в один раз превышает оптимальный. [21] Определение того, имеет ли набор дуг обратной связи алгоритм аппроксимации с постоянным соотношением или необходимо непостоянное соотношение, остается открытой проблемой. [34]

Задача о максимальном ациклическом подграфе имеет простой алгоритм аппроксимации, который обеспечивает коэффициент аппроксимации :

  • Исправление произвольного порядка вершин
  • Разбейте ребра на два ациклических подграфа, один из которых состоит из ребер, направленных в соответствии с порядком, а другой - из ребер, направленных противоположно порядку.
  • Верните больший из двух подграфов.

Это можно улучшить, используя жадный алгоритм выбора порядка. Этот алгоритм находит и удаляет вершину, у которой количество входящих и исходящих ребер находится как можно дальше друг от друга, рекурсивно упорядочивает оставшийся граф, а затем помещает удаленную вершину в один конец полученного порядка. Для графиков с края и вершин, это создает ациклический подграф с края за линейное время, что дает коэффициент аппроксимации . [35] Другой, более сложный алгоритм аппроксимации полиномиальным временем применяется к графам с максимальной степенью и находит ациклический подграф с ребра, что дает коэффициент аппроксимации вида . [36] [37] Когда , коэффициент аппроксимации может быть достигнуто. [38]

Ограниченные входы [ править ]

В ориентированных плоских графах проблема множества дуг обратной связи двойственна проблеме сжатия набора ребер (дисоединения ) , чтобы сделать результирующий граф сильно связным . [39] Эта двойственная задача полиномиально разрешима: [40] и, следовательно, проблема набора плоских дуг с минимальной обратной связью также является проблемой. [41] [40] Это можно решить со временем . [42] Взвешенный вариант проблемы можно решить со временем , [39] или когда веса представляют собой положительные целые числа, которые не превышают числа , во времени . [42] Эти планарные алгоритмы можно распространить на графы, не имеющие графа полезности. в качестве минора графа , используя тот факт, что трехсвязные компоненты этих графов либо плоские, либо имеют ограниченный размер. [26] Плоские графы также были обобщены другим способом на класс ориентированных графов, называемых слабо ациклическими орграфами , определяемыми целостностью определенного многогранника, связанного с их наборами дуг обратной связи . Каждый планарный ориентированный граф является слабо ациклическим в этом смысле, и проблема множества дуг обратной связи может быть решена за полиномиальное время для всех слабо ациклических орграфов. [43]

Приводимые потоковые графы - это еще один класс ориентированных графов, на которых проблема множества дуг обратной связи может быть решена за полиномиальное время. Эти графики описывают поток управления в структурированных программах для многих языков программирования. Хотя структурированные программы часто создают плоские направленные потоковые графы, определение сводимости не требует, чтобы граф был плоским. [44]

Когда проблема набора дуг с минимальной обратной связью ограничивается турнирами , она имеет схему аппроксимации с полиномиальным временем , которая обобщается до взвешенной версии проблемы. [45] Известен также субэкспоненциальный параметризованный алгоритм для взвешенных наборов дуг обратной связи на турнирах. [14] Задача о максимальном ациклическом подграфе для плотных графов также имеет схему аппроксимации за полиномиальное время. Его основные идеи заключаются в том, чтобы применить рандомизированное округление к линейного программирования релаксации задачи и дерандомизировать полученный алгоритм с помощью обходов по расширительным графам . [34] [46]

Твердость [ править ]

NP-твердость [ править ]

Снижение NP -полноты Карпа и Лоулера от покрытия вершин большого желтого графа до минимальной дуги обратной связи, установленной в маленьком синем графе, расширяет каждую желтую вершину на две соседние синие вершины графа, а каждое ненаправленное желтое ребро - на два противоположно направленных ребра. . Минимальное покрытие вершин (верхняя левая и нижняя правая желтые вершины) соответствует набору красной минимальной дуги обратной связи.

Чтобы применить теорию NP-полноты к минимальному набору дуг обратной связи, необходимо изменить проблему с задачи оптимизации (сколько ребер можно удалить, чтобы прервать все циклы) на эквивалентную версию решения с ответом «да» или нет ответа (можно ли удалить края). Таким образом, вариант решения задачи множества дуг обратной связи принимает в качестве входных данных как ориентированный граф, так и число. . Он спрашивает, можно ли разорвать все циклы, удалив не более ребра или, что то же самое, существует ли ациклический подграф с хотя бы края. Эта задача является NP-полной , а это означает, что ни она, ни задача оптимизации не должны иметь алгоритмы с полиномиальным временем. Это была одна из Ричарда М. Карпа первоначальных 21 NP-полной задачи ; его NP-полнота была доказана Карпом и Юджином Лоулером , показав, что входные данные для другой сложной проблемы, проблемы вершинного покрытия , могут быть преобразованы («сокращены») в эквивалентные входные данные для задачи решения множества дуг обратной связи. [47] [48]

Некоторые NP-полные задачи могут стать проще, если их входные данные ограничены особыми случаями. Но для самого важного частного случая задачи о множестве дуг обратной связи, а именно турниров, проблема остается NP-полной. [49] [50]

Неприближаемость [ править ]

Класс сложности APX определяется как состоящий из задач оптимизации, которые имеют алгоритм аппроксимации с полиномиальным временем, обеспечивающий постоянный коэффициент аппроксимации . Хотя такие аппроксимации для задачи набора дуг обратной связи неизвестны, известно, что проблема APX-сложна , а это означает, что точные аппроксимации для нее можно использовать для достижения столь же точных аппроксимаций для всех других задач в APX. В результате доказательства твердости, если только P = NP , он не имеет коэффициента аппроксимации полиномиального времени лучше, чем 1,3606. Это тот же порог жесткости аппроксимации, который известен для вершинного покрытия, и в доказательстве используется редукция Карпа – Лоулера от вершинного покрытия к набору дуг обратной связи, что сохраняет качество аппроксимации. [34] [51] [52] [53] Другими словами, проблема максимального ациклического подграфа также является APX-трудной и NP-трудной для аппроксимации с точностью до коэффициента 65/66 от оптимального. [38]

Трудность аппроксимации этих задач также изучалась при недоказанных предположениях о вычислительной сложности , которые являются стандартными в теории сложности вычислений, но более сильными, чем P ≠ NP. Если гипотеза об уникальных играх верна, то задачу о минимальном наборе дуг обратной связи трудно аппроксимировать за полиномиальное время с точностью до любого постоянного множителя, а задачу о максимальном наборе дуг обратной связи трудно аппроксимировать с точностью до коэффициента , для каждого . [54] За пределами полиномиального времени для алгоритмов аппроксимации, если гипотеза экспоненциального времени верна, то для каждого минимальный набор дуг обратной связи не имеет аппроксимации в пределах коэффициента которое можно вычислить за субэкспоненциальное время . [55]

Теория [ править ]

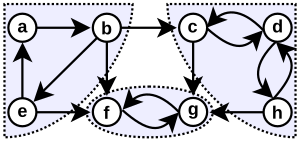
В плоских ориентированных графах проблема множества дуг обратной связи подчиняется теореме о мин-максе : минимальный размер набора дуг обратной связи равен максимальному количеству направленных циклов, не пересекающихся по ребрам, которые можно найти в графе. [41] [56] Это неверно для некоторых других графиков; например, на первой иллюстрации показана ориентированная версия непланарного графа. в котором минимальный размер набора дуг обратной связи равен двум, а максимальное количество направленных циклов, не пересекающихся по краям, - только один.

Каждый граф турнира имеет гамильтонов путь , и гамильтоновы пути один к одному соответствуют минимальным наборам дуг обратной связи, не пересекающимся с соответствующим путем. Гамильтонов путь для набора дуг обратной связи находится путем перестановки его дуг и нахождения топологического порядка результирующего ациклического турнира. Каждая последовательная пара порядка должна быть непересекающейся с наборами дуг обратной связи, поскольку в противном случае можно было бы найти меньший набор дуг обратной связи, перевернув эту пару. Следовательно, такое упорядочение дает путь по дугам исходного турнира, охватывающий все вершины. И наоборот, из любого гамильтонова пути набор ребер, соединяющих более поздние вершины пути с более ранними, образует множество дуг обратной связи. Он минимален, поскольку каждое его ребро принадлежит циклу, ребра гамильтоновых путей которого не пересекаются со всеми другими такими циклами. [57] В турнире может случиться так, что минимальный набор дуг обратной связи и максимальный ациклический подграф оба находятся близко к половине ребер. Точнее, каждый граф турнира имеет набор дуг обратной связи размером , а некоторые турниры требуют размера . [58] для Практически всех турниров размер не менее . [59] Любой направленный ациклический граф может быть встроен как подграф более крупного турнирного графа таким образом, что это уникальный набор дуг турнира с минимальной обратной связью. Размер этого турнира определяется как «обратное число » , а среди ориентированных ациклических графов с тем же числом вершин он наибольший, когда сам по себе является (ациклическим) турниром. [60] [61]

Ориентированный граф имеет эйлеров обход всякий раз, когда он сильно связен и каждая вершина имеет одинаковое количество входящих и исходящих ребер. Для такого графа с края и вершин, размер минимального набора дуг обратной связи всегда не менее . Существует бесконечно много эйлеровых ориентированных графов, для которых эта оценка точна. [62] Если ориентированный граф имеет вершин, с не более чем тремя ребрами на вершину, то он имеет набор дуг обратной связи не более ребер, а некоторые графы требуют именно столько. Если ориентированный граф имеет ребер, не более четырех ребер на вершину, то он имеет набор дуг обратной связи не более ребер, а некоторые графы требуют именно столько. [63]

Ссылки [ править ]

  1. ^ «Основная сетка – мужчины» , Рио, 2016 г. , Международная федерация волейбола , заархивировано из оригинала 23 декабря 2016 г. , получено 14 ноября 2021 г.
  2. ↑ Перейти обратно: Перейти обратно: а б с Хьюберт, Лоуренс (1976), «Сериация с использованием асимметричных мер близости», Британский журнал математической и статистической психологии , 29 (1): 32–52, doi : 10.1111/j.2044-8317.1976.tb00701.x , MR   0429180
  3. ↑ Перейти обратно: Перейти обратно: а б с Ремидж, Рассел-младший; Томпсон, Вашингтон-младший (1966), «Рейтинги парных сравнений максимального правдоподобия», Biometrika , 53 (1–2): 143–149, doi : 10.1093/biomet/53.1-2.143 , JSTOR   2334060 , MR   0196854 , PMID   5964054
  4. ^ Годдард, Стивен Т. (1983), «Рейтинг в турнирах и групповом принятии решений», Management Science , 29 (12): 1384–1392, doi : 10.1287/mnsc.29.12.1384 , MR   0809110 ; обратите внимание, что алгоритм, предложенный Годдардом для определения рейтингов с минимальным нарушением, неверен.
  5. ^ Вазири, Бабак; Дабадгао, Шонак; Да, Юверн; Морин, Томас Л. (январь 2018 г.), «Свойства методов спортивного ранжирования» (PDF) , Журнал Общества операционных исследований , 69 (5): 776–787, doi : 10.1057/s41274-017-0266-8 , S2CID   51887586
  6. ^ Копперсмит, Дон ; Флейшер, Лиза К.; Рурда, Атри (2010), «Упорядочение по взвешенному количеству побед дает хороший рейтинг для взвешенных турниров», Транзакции ACM по алгоритмам , 6 (3): A55:1–A55:13, doi : 10.1145/1798596.1798608 , MR   2682624 , S2CID   18416
  7. ^ Сейфарт, Роберт М. (ноябрь 1976 г.), «Социальные отношения среди взрослых самок павианов», Animal Behavior , 24 (4): 917–938, doi : 10.1016/s0003-3472(76)80022-x , S2CID   54284406
  8. ^ Эстеп, DQ; Кроуэлл-Дэвис, СЛ; Эрл-Костелло, Южная Каролина; Бити, С.А. (январь 1993 г.), «Изменения в социальном поведении кобыл тяжеловозов (Equus caballus), совпадающие с вырождением жеребят», Applied Animal Behavior Science , 35 (3): 199–213, doi : 10.1016/0168-1591(93) 90137-э
  9. ^ Эйкворт, Джордж К. (апрель 2019 г.), «Доминирование таракана (Науфоэта)», Поведение насекомых , CRC Press, стр. 120–126, doi : 10.1201/9780429049262-18 , S2CID   203898549
  10. ^ Слейтер, Патрик (1961), «Несоответствия в графике парных сравнений», Biometrika , 48 (3–4): 303–312, doi : 10.1093/biomet/48.3-4.303 , JSTOR   2332752
  11. ^ Бранк, HD (1960), «Математические модели для ранжирования на основе парных сравнений», Журнал Американской статистической ассоциации , 55 (291): 503–520, doi : 10.2307/2281911 , JSTOR   2281911 , MR   0115242 ; опубликовано в предварительной форме как документ ASTIA № AD 206 573, ВВС США, Управление научных исследований, ноябрь 1958 г., hdl : 2027/mdp.39015095254010
  12. ^ Томпсон, Вашингтон младший; Ремейдж, Рассел-младший (1964), «Рейтинги на основе парных сравнений», Annals of Mathematical Статистика , 35 (2): 739–747, doi : 10.1214/aoms/1177703572 , JSTOR   2238526 , MR   0161419
  13. ^ Кемени, Джон Г. (осень 1959 г.), «Математика без чисел», Дедал , 88 (4): 577–591, JSTOR   20026529
  14. ↑ Перейти обратно: Перейти обратно: а б Карпински, Марек ; Шуди, Уоррен (2010), «Более быстрые алгоритмы для турнира по набору дуг обратной связи, агрегации рангов Кемени и турнира по промежуткам», в Чеонг, Отфрид ; Чва, Кён Ён; Пак, Кунсу (ред.), «Алгоритмы и вычисления – 21-й международный симпозиум», ISAAC 2010, остров Чеджу, Корея, 15–17 декабря 2010 г., Материалы, часть I , конспекты лекций по информатике, том. 6506, Springer, стр. 3–14, arXiv : 1006.4396 , doi : 10.1007/978-3-642-17517-6_3 , S2CID   16512997
  15. ↑ Перейти обратно: Перейти обратно: а б Унгер, Стивен Х. (26 апреля 1957 г.), Исследование асинхронных сетей с логической обратной связью , Технические отчеты, том. 320, Массачусетский технологический институт, Исследовательская лаборатория электроники, hdl : 1721.1/4763
  16. ^ Ферер, Джон Р.; Джордан, Гарри Ф. (декабрь 1995 г.), «Размещение часовых вентилей во времяпролетных оптоэлектронных схемах», Applied Optics , 34 (35): 8125–8136, Bibcode : 1995ApOpt..34.8125F , doi : 10.1364/ao .34.008125 , PMID   21068927
  17. ^ Розен, Эдвард М.; Хенли, Эрнест Дж. (лето 1968 г.), «Новая стехиометрия» , Chemical Engineering Education , 2 (3): 120–125, заархивировано из оригинала 02 августа 2021 г. , получено 2 августа 2021 г.
  18. ^ Ди Баттиста, Джузеппе; Идс, Питер ; Тамассия, Роберто ; Толлис, Иоаннис Г. (1998), «Многослойные рисунки орграфов», Рисование графиков: алгоритмы визуализации графов , Прентис Холл , стр. 265–302, ISBN  978-0-13-301615-4
  19. ^ Бастерт, Оливер; Матушевский, Кристиан (2001), «Многослойные рисунки орграфов», Кауфманн, Майкл; Вагнер, Доротея (ред.), Рисование графиков: методы и модели , Конспекты лекций по информатике, том. 2025, Springer-Verlag, стр. 87–120, номер документа : 10.1007/3-540-44969-8_5.
  20. ^ Деметреску, Камил; Финокки, Ирен (2001), «Разорвите «правильные» циклы и получите «лучший» рисунок», ACM Journal of Experimental Algorithmics , 6 : 171–182, MR   2027115.
  21. ↑ Перейти обратно: Перейти обратно: а б с Эвен, Г.; Наор, Дж .; Шибер, Б .; Судан, М. (1998), «Аппроксимация наборов минимальной обратной связи и мультиразрезов в ориентированных графах», Algorithmica , 20 (2): 151–174, doi : 10.1007/PL00009191 , MR   1484534 , S2CID   2437790
  22. ↑ Перейти обратно: Перейти обратно: а б Минура, Тошими (1982), «Возвращение к предотвращению тупиков», Journal of the ACM , 29 (4): 1023–1048, doi : 10.1145/322344.322351 , MR   0674256 , S2CID   5284738
  23. ^ Мишра, Сунака; Сикдар, Крипасиндху (2004), «Об аппроксимируемости линейного порядка и связанных с ним задачах NP-оптимизации на графах», Discrete Applied Mathematics , 136 (2–3): 249–269, doi : 10.1016/S0166-218X(03)00444- Х , МР   2045215
  24. ↑ Перейти обратно: Перейти обратно: а б Хехт, Майкл (2017), «Точные локализации наборов обратной связи», Теория вычислительных систем , 62 (5): 1048–1084, arXiv : 1702.07612 , doi : 10.1007/s00224-017-9777-6 , S2CID   18394348
  25. ^ Парк, С.; Акерс, С.Б. (1992), «Эффективный метод поиска минимального набора дуг обратной связи в ориентированных графах», Труды Международного симпозиума IEEE по схемам и системам 1992 года (ISCAS '92) , том. 4, стр. 1863–1866, номер документа : 10.1109/iscas.1992.230449 , S2CID   122603659 .
  26. ↑ Перейти обратно: Перейти обратно: а б Нутов, Зеев; Пенн, Михал (2000), «О целостности, устойчивости и составе упаковок и покрытий дициклов», Journal of Combinatorial Optimization , 4 (2): 235–251, doi : 10.1023/A:1009802905533 , MR   1772828 , S2CID   207632524
  27. ^ Янгер, Д. (1963), «Минимальные наборы дуг обратной связи для ориентированного графа», IEEE Transactions on Circuit Theory , 10 (2): 238–245, doi : 10.1109/tct.1963.1082116
  28. ^ Лоулер, Э. (1964), «Комментарий к минимальным наборам дуг обратной связи», IEEE Transactions on Circuit Theory , 11 (2): 296–297, doi : 10.1109/tct.1964.1082291
  29. ↑ Перейти обратно: Перейти обратно: а б Бодлендер, Ганс Л .; Фомин Федор Владимирович; Костер, Арье MCA; Крач, Дитер; Тиликос, Димитриос М. (2012), «Заметка о точных алгоритмах для задач упорядочения вершин на графах», Theory of Computing Systems , 50 (3): 420–432, doi : 10.1007/s00224-011-9312-0 , hdl : 1956/4556 , МР   2885638 , S2CID   9967521
  30. ^ Чен, Цзянер; Лю, Ян; Лу, Сунцзянь; О'Салливан, Барри; Разгон, Игорь (2008), «Алгоритм с фиксированными параметрами для задачи множества вершин с направленной обратной связью», Журнал ACM , 55 (5): 1–19, doi : 10.1145/1411509.1411511 , S2CID   1547510
  31. ^ Бонами, Марта; Ковалик, Лукаш; Недерлоф, Йеспер; Пилипчук, Михал; Сокала, Аркадиуш; Врочна, Марцин (2018), «О множестве вершин с направленной обратной связью, параметризованном шириной дерева», в Брандштедте, Андреас; Кёлер, Эккехард; Меер, Клаус (ред.), Теоретико-графовые концепции в информатике - 44-й международный семинар, WG 2018, Котбус, Германия, 27–29 июня 2018 г., Труды , Конспекты лекций по информатике, том. 11159, Springer, стр. 65–78, arXiv : 1707.01470 , doi : 10.1007/978-3-030-00256-5_6 , S2CID   8008855
  32. ^ Лин, Лишин; Сахни, Сартадж (1989), «Проблемы справедливого удаления ребер», IEEE Transactions on Computers , 38 (5): 756–761, doi : 10.1109/12.24280 , MR   0994519
  33. ^ Швиковский, Бенно; Спекенмейер, Эвальд (2002), «О перечислении всех минимальных решений задач с обратной связью», Discrete Applied Mathematics , 117 (1–3): 253–265, doi : 10.1016/S0166-218X(00)00339-5 , MR   1881280
  34. ↑ Перейти обратно: Перейти обратно: а б с Крещенци, Пьерлуиджи; Канн, Вигго; Халльдорссон, Магнус; Карпински, Марек ; Воегингер, Герхард (2000), «Набор дуг минимальной обратной связи» , сборник задач оптимизации NP , заархивировано из оригинала 29 июля 2021 г. , получено 29 июля 2021 г.
  35. ^ Идс, Питер ; Линь, Сюэмин; Смит, В.Ф. (1993), «Быстрая и эффективная эвристика для решения задачи множества дуг обратной связи» , Information Processing Letters , 47 (6): 319–323, doi : 10.1016/0020-0190(93)90079-O , MR   1256786 , заархивировано из оригинала 22 октября 2020 г. , получено 1 августа 2021 г.
  36. ^ Бергер, Бонни ; Шор, Питер В. (1997), «Точные границы для проблемы максимального ациклического подграфа», Журнал алгоритмов , 25 (1): 1–18, doi : 10.1006/jagm.1997.0864 , ​​MR   1474592
  37. ^ Хассин, Рафаэль; Рубинштейн, Шломи (1994), «Приближения к проблеме максимального ациклического подграфа», Information Processing Letters , 51 (3): 133–140, doi : 10.1016/0020-0190(94)00086-7 , MR   1290207
  38. ↑ Перейти обратно: Перейти обратно: а б Ньюман, Аланта (июнь 2000 г.), Аппроксимация максимального ациклического подграфа (магистерская диссертация), Массачусетский технологический институт, hdl : 1721.1/86548 , цитируется Гурусвами и др. (2011)
  39. ↑ Перейти обратно: Перейти обратно: а б Габоу, Гарольд Н. (1995), «Центроиды, представления и субмодулярные потоки», Journal of Algorithms , 18 (3): 586–628, doi : 10.1006/jagm.1995.1022 , MR   1334365
  40. ↑ Перейти обратно: Перейти обратно: а б Франк, Андраш (1981), «Как сделать орграф сильно связным», Combinatorica , 1 (2): 145–153, doi : 10.1007/BF02579270 , MR   0625547 , S2CID   27825518
  41. ↑ Перейти обратно: Перейти обратно: а б Луккези, CL; Янгер, Д.Х. (1978), «Теорема о минимаксе для ориентированных графов», Журнал Лондонского математического общества , вторая серия, 17 (3): 369–374, doi : 10.1112/jlms/s2-17.3.369 , MR   0500618
  42. ↑ Перейти обратно: Перейти обратно: а б Габоу, Гарольд Н. (1993), «Структура алгоритмов масштабирования стоимости для задач субмодульного потока», 34-й ежегодный симпозиум по основам информатики, Пало-Альто, Калифорния, США, 3-5 ноября 1993 г. , Компьютерное общество IEEE, стр. . 449–458, doi : 10.1109/SFCS.1993.366842 , MR   1328441 , S2CID   32162097.
  43. ^ Гретшель, Мартин ; Юнгер, Майкл; Рейнельт, Герхард (1985), «О многограннике ациклического подграфа», Mathematical Programming , 33 (1): 28–42, doi : 10.1007/BF01582009 , MR   0809747 , S2CID   206798683
  44. ^ Рамачандран, Виджая (1988), «Нахождение минимального набора дуг обратной связи в приводимых потоковых графах», Journal of Algorithms , 9 (3): 299–313, doi : 10.1016/0196-6774(88)90022-3 , MR   0955140
  45. ^ Кеньон-Матье, Клэр ; Шуди, Уоррен (2007), «Как ранжировать с небольшим количеством ошибок: PTAS для дуги взвешенной обратной связи, установленной на турнирах», Джонсон, Дэвид С .; Файги, Уриэль (ред.), Труды 39-го ежегодного симпозиума ACM по теории вычислений, Сан-Диего, Калифорния, США, 11–13 июня 2007 г. , стр. 95–103, doi : 10.1145/1250790.1250806 , S2CID   9436948 , ECCC   ТР06-144 ; см. также расширенную версию автора. Архивировано 15 января 2009 г. на Wayback Machine.
  46. ^ Арора, Санджив ; Фриз, Алан ; Каплан, Хаим (2002), «Новая процедура округления задачи назначения с применением к задачам плотного расположения графов» , Mathematical Programming , 92 (1): 1–36, doi : 10.1007/s101070100271 , MR   1892295 , S2CID   3207086 , в архиве из оригинала от 3 августа 2021 г. , получено 3 августа 2021 г.
  47. ^ Карп, Ричард М. (1972), «Сводимость комбинаторных задач», Сложность компьютерных вычислений , Proc. Симпозиумы. IBM Томас Дж. Уотсон Рез. Центр, Йорктаун-Хайтс, Нью-Йорк, Нью-Йорк: Пленум, стр. 85–103.
  48. ^ Гэри, Майкл Р .; Джонсон, Дэвид С. (1979), «A1.1: GT8», Компьютеры и трудноразрешимые проблемы: Руководство по теории NP-полноты , WH Freeman, p. 192, ИСБН  0-7167-1045-5
  49. ^ Алон, Нога (2006), «Рейтинговые турниры», SIAM Journal on Discrete Mathematics , 20 (1): 137–142, doi : 10.1137/050623905 , MR   2257251
  50. ^ Шарбит, Пьер; Томассе, Стефан; Йео, Андерс (2007), «Проблема с набором дуг минимальной обратной связи NP-сложна для турниров» (PDF) , Combinatorics, Probability and Computing , 16 (1): 1–4, doi : 10.1017/S0963548306007887 , MR   2282830 , S2CID   36539840
  51. ^ Озиелло, Г .; Д'Атри, А.; Протаси, М. (1980), «Сокращения, сохраняющие структуру среди задач выпуклой оптимизации», Журнал компьютерных и системных наук , 21 (1): 136–153, doi : 10.1016/0022-0000(80)90046-X , MR   0589808
  52. ^ Канн, Вигго (1992), Об аппроксимируемости задач NP-полной оптимизации (PDF) (докторская диссертация), Департамент численного анализа и вычислительной техники, Королевский технологический институт, Стокгольм, в архиве (PDF) с оригинала 29 декабря 2010 г. , получено 11 октября 2007 г.
  53. ^ Динур, Ирит ; Сафра, Сэмюэл (2005), «О сложности аппроксимации минимального вершинного покрытия» (PDF) , Annals of Mathematics , 162 (1): 439–485, doi : 10.4007/annals.2005.162.439 , заархивировано (PDF) из оригинал от 20 сентября 2009 г. , получено 29 июля 2021 г .; предварительная версия в Динур, Ирит ; Сафра, Сэмюэл (2002), «Важность предвзятости», в Рейфе, Джон Х. (ред.), Труды 34-го ежегодного симпозиума ACM по теории вычислений, 19–21 мая 2002 г., Монреаль, Квебек, Канада. , стр. 33–42, doi : 10.1145/509907.509915 , S2CID   1235048
  54. ^ Гурусвами, Венкатесан ; Хостад, Йохан ; Манокаран, Раджекар; Рагхавендра, Прасад; Чарикар, Моисей (2011), «Преодолеть случайный порядок сложно: каждый упорядочивающий CSP устойчив к аппроксимации» (PDF) , SIAM Journal on Computing , 40 (3): 878–914, doi : 10.1137/090756144 , MR   2823511 , в архиве (PDF) из оригинала 31 июля 2021 г. , получено 31 июля 2021 г.
  55. ^ Бонне, Эдуард; Пашос, Вангелис Т. (2018), «Разреженность и субэкспоненциальная аппроксимация», Acta Informatica , 55 (1): 1–15, arXiv : 1402.2843 , doi : 10.1007/s00236-016-0281-2 , MR   3757549 , S2CID   3136275
  56. ^ Ловас, Ласло (1976), «О двух минимаксных теоремах в графе», Журнал комбинаторной теории , серия B, 21 (2): 96–103, doi : 10.1016/0095-8956(76)90049-6 , MR   0427138
  57. ^ Бар-Ной, Амоц; Наор, Джозеф (1990), «Сортировка, наборы с минимальной обратной связью и пути Гамильтона в турнирах», SIAM Journal on Discrete Mathematics , 3 (1): 7–20, doi : 10.1137/0403002 , MR   1033709
  58. ^ Спенсер, Дж. (1980), «Оптимальное ранжирование турниров без рейтинга», Periodica Mathematica Hungarica , 11 (2): 131–144, doi : 10.1007/BF02017965 , MR   0573525 , S2CID   119894999
  59. ^ Фернандес де ла Вега, В. (1983), «О максимальной мощности согласованного набора дуг в случайном турнире», Журнал комбинаторной теории , серия B, 35 (3): 328–332, doi : 10.1016/0095 -8956(83)90060-6 , МР   0735201
  60. ^ Бартелеми, Жан-Пьер; Юдри, Оливье; Исаак, Гарт; Робертс, Фред С .; Тесман, Барри (1995), «Реверсивное число орграфа», Discrete Applied Mathematics , 60 (1–3): 39–76, doi : 10.1016/0166-218X(94)00042-C , MR   1339075
  61. ^ Исаак, Гарт; Нараян, Даррен А. (2004), «Классификация турниров, в которых ациклический турнир является минимальным набором дуг обратной связи» , Information Processing Letters , 92 (3): 107–111, doi : 10.1016/j.ipl.2004.07.001 , МР   2095357
  62. ^ Хуан, Хао; Ма, Цзе; Шапира, Асаф; Судаков, Бенни ; Юстер, Рафаэль (2013), «Большие множества дуг обратной связи, подграфы с высокой минимальной степенью и длинные циклы в эйлеровых орграфах», Combinatorics, Probability and Computing , 22 (6): 859–873, arXiv : 1202.2602 , doi : 10.1017/S0963548313000394 , hdl : 20.500.11850/73894 , MR   3111546 , S2CID   7967738
  63. ^ Ханауэр, Катрин; Бранденбург, Франц-Иосиф; Ауэр, Кристофер (2013), «Точные верхние границы для минимальных наборов дуг обратной связи регулярных графов», Брандштедт, Андреас; Янсен, Клаус; Райщук, Рюдигер (ред.), Теоретико-графовые концепции в информатике - 39-й международный семинар, WG 2013, Любек, Германия, 19–21 июня 2013 г., Переработанные статьи , Конспекты лекций по информатике, том. 8165, Springer, стр. 298–309, номер документа : 10.1007/978-3-642-45043-3_26 , MR   3139198.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Feedback_arc_set&oldid=1221317774"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: 94d87be8a6be2fa30d530c5b2cddd40c__1714359180
URL1:https://arc.ask3.ru/arc/aa/94/0c/94d87be8a6be2fa30d530c5b2cddd40c.html
Заголовок, (Title) документа по адресу, URL1:
Feedback arc set - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)