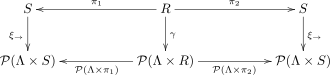Бисимуляция

В теоретической информатике бисимуляция бинарное — это отношение между системами перехода состояний , связывающее системы, которые ведут себя одинаково, при этом одна система моделирует другую и наоборот.

Интуитивно две системы считаются биподобными, если они, предполагая, что мы рассматриваем их как игру по некоторым правилам, соответствуют ходам друг друга. В этом смысле наблюдатель не может отличить каждую из систем от другой.

Формальное определение

Учитывая помеченную систему перехода состояний ( $S$, $\Lambda$, →),где $S$ представляет собой совокупность состояний, $\Lambda$ — это набор меток, а → — это набор помеченных переходов (т. е. подмножество $S\times \Lambda \times S$),бисимуляция бинарное — это отношение $R\subseteq S\times S$,такой, что оба $R$ и его обратная сторона $R^{T}$ являются симуляциями . Отсюда следует, что симметричное замыкание бисимуляции есть бисимуляция и что каждая симметричная симуляция есть бисимуляция. Таким образом, некоторые авторы определяют бисимуляцию как симметричную симуляцию.

Эквивалентно, $R$ является бисимуляцией тогда и только тогда, когда для каждой пары состояний $(p,q)$ в $R$ и все метки λ в $\Lambda$:

• если $p\mathrel {\overset {\lambda }{\rightarrow }} p'$, то есть $q\mathrel {\overset {\lambda }{\rightarrow }} q'$ такой, что $(p',q')\in R$;
• если $q\mathrel {\overset {\lambda }{\rightarrow }} q'$, то есть $p\mathrel {\overset {\lambda }{\rightarrow }} p'$ такой, что $(p',q')\in R$.

Учитывая два состояния $p$ и $q$ в $S$, $p$ похож на ​ $q$, написано $p\,\sim \,q$, тогда и только тогда, когда существует бисимуляция $R$ такой, что $(p,q)\in R$. Это означает, что соотношение биподобия $\,\sim \,$ является объединением всех бисимуляций: $(p,q)\in \,\sim \,$ именно тогда, когда $(p,q)\in R$ для некоторой бисимуляции $R$.

Множество бисимуляций замкнуто по объединению; следовательно, отношение биподобия само по себе является бисимуляцией. Поскольку это объединение всех бисимуляций, это уникальная и крупнейшая бисимуляция. Бисимуляции также замкнуты при рефлексивном, симметричном и транзитивном замыкании; следовательно, наибольшая бисимуляция должна быть рефлексивной, симметричной и транзитивной. Отсюда следует, что наибольшая бисимуляция — биподобие — есть отношение эквивалентности .

Альтернативные определения

Реляционное определение

Бисимуляцию можно определить с точки зрения композиции отношений следующим образом.

Учитывая маркированную систему перехода состояний $(S,\Lambda ,\rightarrow )$, бисимуляции отношение является бинарным отношением $R$ над $S$ (т.е. $R$ ⊆ $S$ × $S$) такой, что $\forall \lambda \in \Lambda$

$$R\ ;\ {\overset {\lambda }{\rightarrow }}\quad {\subseteq }\quad {\overset {\lambda }{\rightarrow }}\ ;\ R$$

и

$$R^{-1}\ ;\ {\overset {\lambda }{\rightarrow }}\quad {\subseteq }\quad {\overset {\lambda }{\rightarrow }}\ ;\ R^{-1}$$

Из монотонности и непрерывности композиции отношений сразу следует, что множество бисимуляций замкнуто относительно объединений ( объединений в ЧУ отношений), а простой алгебраический расчет показывает, что отношение биподобия — объединение всех бисимуляций — есть отношение эквивалентности. Это определение и связанное с ним понимание биподобия можно интерпретировать в любом инволютивном кванте .

Определение фиксированной точки

Биподобие также можно определить теоретико -порядковым способом, с точки зрения теории неподвижных точек , точнее, как наибольшую неподвижную точку определенной функции, определенной ниже.

Учитывая помеченную систему перехода состояний ( $S$, Λ, →), определим $F:{\mathcal {P}}(S\times S)\to {\mathcal {P}}(S\times S)$ быть функцией бинарных отношений над $S$ к бинарным отношениям над $S$, следующее:

Позволять $R$ быть любым бинарным отношением над $S$. $F(R)$ определяется как множество всех пар $(p,q)$ в $S$ × $S$ такой, что:

$$\forall \lambda \in \Lambda .\,\forall p'\in S.\,p{\overset {\lambda }{\rightarrow }}p'\,\Rightarrow \,\exists q'\in S.\,q{\overset {\lambda }{\rightarrow }}q'\,{\textrm {and}}\,(p',q')\in R$$

и

$$\forall \lambda \in \Lambda .\,\forall q'\in S.\,q{\overset {\lambda }{\rightarrow }}q'\,\Rightarrow \,\exists p'\in S.\,p{\overset {\lambda }{\rightarrow }}p'\,{\textrm {and}}\,(p',q')\in R$$

Тогда биподобие определяется как наибольшая фиксированная точка $F$.

Определение игры Эренфойхта–Фрэссе

Бисимуляцию также можно рассматривать как игру между двумя игроками: нападающим и защитником.

«Атакующий» ходит первым и может выбрать любой допустимый переход. $\lambda$, от $(p,q)$. То есть,

$$(p,q){\overset {\lambda }{\rightarrow }}(p',q)$$

или

$$(p,q){\overset {\lambda }{\rightarrow }}(p,q')$$

Затем «Защитник» должен попытаться соответствовать этому переходу. $\lambda$ от любого $(p',q)$ или $(p,q')$ в зависимости от хода нападающего.То есть они должны найти $\lambda$ такой, что:

$$(p',q){\overset {\lambda }{\rightarrow }}(p',q')$$

или

$$(p,q'){\overset {\lambda }{\rightarrow }}(p',q')$$

Атакующий и защищающийся продолжают действовать поочередно до тех пор, пока:

• Защитник не может найти никаких допустимых переходов, соответствующих движению атакующего. В этом случае побеждает нападающий.
• Игра доходит до штатов $(p,q)$ которые оба «мертвы» (т. е. нет переходов из любого состояния). В этом случае побеждает защищающийся
• Игра продолжается вечно, и в этом случае побеждает защитник.
• Игра доходит до штатов $(p,q)$, которые уже были посещены. Это эквивалентно бесконечной игре и засчитывается как победа защитника.

Согласно приведенному выше определению, система является бисимуляцией тогда и только тогда, когда существует выигрышная стратегия для защищающегося.

Коалгебраическое определение

Бисимуляция для систем с переходом состояний является частным случаем коалгебраической бисимуляции для типа ковариантного функтора степенного множества .Обратите внимание, что каждая система перехода состояний $(S,\Lambda ,\rightarrow )$ может быть биективно отображен в функцию $\xi _{\rightarrow }$ от $S$ к мощности набору $S$ индексируется $\Lambda$ написано как ${\mathcal {P}}(\Lambda \times S)$, определяемый

$$p\mapsto \{(\lambda ,q)\in \Lambda \times S:p{\overset {\lambda }{\rightarrow }}q\}.$$

Позволять $\pi _{i}\colon S\times S\to S$ быть $i$-я проекция , отображение $(p,q)$ к $p$ и $q$ соответственно для $i=1,2$; и ${\mathcal {P}}(\Lambda \times \pi _{1})$ передний образ $\pi _{1}$ определяется удалением третьего компонента

$$P\mapsto \{(\lambda ,p)\in \Lambda \times S:\exists q.(\lambda ,p,q)\in P\}$$

где $P$ является подмножеством $\Lambda \times S\times S$. Аналогично для ${\mathcal {P}}(\Lambda \times \pi _{2})$.

Используя приведенные выше обозначения, соотношение $R\subseteq S\times S$ это бисимуляция переходной системы $(S,\Lambda ,\rightarrow )$ тогда и только тогда, когда существует переходная система $\gamma \colon R\to {\mathcal {P}}(\Lambda \times R)$ по отношению $R$ такая, что диаграмма

ездит на работу, то есть для $i=1,2$, уравнения

$$\xi _{\rightarrow }\circ \pi _{i}={\mathcal {P}}(\Lambda \times \pi _{i})\circ \gamma$$

держатьгде $\xi _{\rightarrow }$ является функциональным представлением $(S,\Lambda ,\rightarrow )$.

Варианты бисимуляции

В особых контекстах понятие бисимуляции иногда уточняется путем добавления дополнительных требований или ограничений. Примером может служить бисимуляция заикания , в которой один переход одной системы может быть сопоставлен с несколькими переходами другой системы при условии, что промежуточные состояния эквивалентны начальному состоянию («заикания»).

Другой вариант применяется, если система перехода состояний включает в себя понятие молчаливого (или внутреннего ) действия, часто обозначаемого $\tau$, то есть действия, которые не видны внешним наблюдателям, тогда бисимуляцию можно ослабить до слабой бисимуляции , в которой, если два состояния $p$ и $q$ биподобны, и существует некоторое количество внутренних действий, ведущих из $p$ в какое-то государство $p'$ тогда должно существовать государство $q'$ такое, что существует некоторое количество (возможно, ноль) внутренних действий, ведущих из $q$ к $q'$. Отношение ${\mathcal {R}}$ на процессах является слабой бисимуляцией, если выполняется следующее (при этом ${\mathcal {S}}\in \{{\mathcal {R}},{\mathcal {R}}^{-1}\}$, и $a,\tau$ являющийся наблюдаемым и немым переходом соответственно):

$$\forall p,q.\quad (p,q)\in {\mathcal {S}}\Rightarrow p{\stackrel {\tau }{\rightarrow }}p'\Rightarrow \exists q'.\quad q{\stackrel {\tau ^{\ast }}{\rightarrow }}q'\wedge (p',q')\in {\mathcal {S}}$$

$$\forall p,q.\quad (p,q)\in {\mathcal {S}}\Rightarrow p{\stackrel {a}{\rightarrow }}p'\Rightarrow \exists q'.\quad q{\stackrel {\tau ^{\ast }a\tau ^{\ast }}{\rightarrow }}q'\wedge (p',q')\in {\mathcal {S}}$$

Это тесно связано к понятию бисимуляции « до » отношения.

Обычно, если система перехода состояний дает операционную семантику языка программирования , то точное определение бисимуляции будет зависеть от ограничений языка программирования. Поэтому, как правило, может существовать более одного вида отношений бисимуляции (соответственно биподобия) в зависимости от контекста.

Бисимуляция и модальная логика

Поскольку модели Крипке представляют собой частный случай (помеченных) систем с переходом состояний, бисимуляция также является темой модальной логики . По сути, модальная логика — это фрагмент логики первого порядка, инвариантный относительно бисимуляции ( теорема Ван Бентема ).

Алгоритм

Проверка того, что две конечные переходные системы являются биподобными, может быть выполнена за полиномиальное время . Самые быстрые алгоритмы имеют квазилинейное время и используют уточнение разделения путем сведения к задаче самого грубого разделения.

См. также

• Предзаказ моделирования
• Отношение конгруэнтности
• Вероятностное бисимуляция

Дальнейшее чтение

• Парк, Дэвид (1981). «Параллелизм и автоматы на бесконечных последовательностях». В Деуссене, Питер (ред.). Теоретическая информатика . Материалы 5-й конференции GI, Карлсруэ. Конспекты лекций по информатике . Том. 104. Шпрингер-Верлаг . стр. 167–183. дои : 10.1007/BFb0017309 . ISBN  978-3-540-10576-3 .
• Милнер, Робин (1989). Коммуникация и параллелизм . Прентис Холл . ISBN  0-13-114984-9 .
• Санджорджи, Давиде (2011). Введение в бисимуляцию и коиндукцию . Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  9781107003637 . OCLC   773040572 .

Внешние ссылки

Программные инструменты

• CADP : инструменты для минимизации и сравнения систем с конечными состояниями в соответствии с различными бисимуляциями.
• mCRL2 : инструменты для минимизации и сравнения систем с конечным числом состояний в соответствии с различными бисимуляциями.
• Игра Бисимуляция Игра