Квадратичная неограниченная бинарная оптимизация

Квадратичная неограниченная бинарная оптимизация ( QUBO ), также известная как неограниченное двоично-квадратичное программирование ( UBQP ), представляет собой задачу комбинаторной оптимизации с широким спектром приложений от финансов и экономики до машинного обучения . QUBO — это NP-сложная задача, и для многих классических задач теоретической информатики , таких как максимальный разрез , раскраска графа и проблема разделения , были сформулированы вложения в QUBO. Вложения для моделей машинного обучения включают машины опорных векторов , кластеризацию и вероятностные графические модели . Более того, из-за своей тесной связи с моделями Изинга , QUBO представляет собой центральный класс проблем адиабатических квантовых вычислений , где он решается с помощью физического процесса, называемого квантовым отжигом .

Определение

Набор двоичных векторов фиксированной длины $n>0$ обозначается $\mathbb {B} ^{n}$, где $\mathbb {B} =\lbrace 0,1\rbrace$ — это набор двоичных значений (или битов ). Нам дана вещественная верхняя треугольная матрица $Q\in \mathbb {R} ^{n\times n}$, чьи записи $Q_{ij}$ определить вес для каждой пары индексов $i,j\in \lbrace 1,\dots ,n\rbrace$ внутри бинарного вектора. Мы можем определить функцию $f_{Q}:\mathbb {B} ^{n}\rightarrow \mathbb {R}$ который присваивает значение каждому двоичному вектору через

$f_{Q}(x)=x^{\top }Qx=\sum _{i=1}^{n}\sum _{j=i}^{n}Q_{ij}x_{i}x_{j}$

Интуитивно вес $Q_{ij}$ добавляется, если оба $x_{i}$ и $x_{j}$ иметь значение 1. Когда $i=j$, значения $Q_{ii}$ добавляются, если $x_{i}=1$, как $x_{i}x_{i}=x_{i}$ для всех $x_{i}\in \mathbb {B}$.

Задача QUBO состоит в нахождении двоичного вектора $x^{*}$ это минимально по отношению к $f_{Q}$, а именно

$\forall x\in \mathbb {B} ^{n}:~f_{Q}(x^{*})\leq f_{Q}(x)$

В общем, $x^{*}$ не является уникальным, то есть может существовать набор минимизирующих векторов с равным значением относительно $f_{Q}$. Сложность QUBO возникает из-за количества оцениваемых двоичных векторов-кандидатов, а именно: $|\mathbb {B} ^{n}|=2^{n}$ растет в геометрической прогрессии $n$.

Иногда QUBO определяют как задачу максимизации $f_{Q}$, что эквивалентно минимизации $f_{-Q}=-f_{Q}$.

Характеристики

QUBO является масштабно-инвариантным для положительных факторов. $\alpha >0$, которые оставляют оптимум $x^{*}$ без изменений:

$f_{\alpha Q}(x)=\sum _{i\leq j}(\alpha Q_{ij})x_{i}x_{j}=\alpha \sum _{i\leq j}Q_{ij}x_{i}x_{j}=\alpha f_{Q}(x)$

В своей общей форме задача QUBO является NP-трудной и не может быть эффективно решена ни одним алгоритмом с полиномиальным временем. Однако существуют полиномиально разрешимые частные случаи, когда $Q$ имеет определенные свойства, например:

• Если все коэффициенты положительны, оптимум тривиально $x^{*}=(0,\dots ,0)$. Аналогично, если все коэффициенты отрицательны, оптимум равен $x^{*}=(1,\dots ,1)$.
• Если $Q$ диагонально , биты можно оптимизировать независимо , и проблема разрешима в ${\mathcal {O}}(n)$. Оптимальные назначения переменных просто $x_{i}^{*}=1$ если $Q_{ii}<0$, и $x_{i}^{*}=0$ в противном случае.
• Если все недиагональные элементы $Q$ неположительны, соответствующая задача QUBO разрешима за полиномиальное время.

QUBO можно решить с помощью целочисленного линейного программирования, решателей таких как CPLEX или Gurobi Optimizer . Это возможно, поскольку QUBO можно переформулировать как задачу бинарной оптимизации с линейными ограничениями. Для этого замените произведение $x_{i}x_{j}$ дополнительной двоичной переменной $z_{ij}\in \{0,1\}$ и добавьте ограничения $x_{i}\geq z_{ij}$, $x_{j}\geq z_{ij}$ и $x_{i}+x_{j}-1\leq z_{ij}$. Обратите внимание, что $z_{ij}$ также может быть релаксирован до непрерывных переменных в пределах нуля и единицы.

Приложения

QUBO — это структурно простая, но вычислительно сложная задача оптимизации. Его можно использовать для кодирования широкого спектра задач оптимизации из различных научных областей.

Кластерный анализ

Бинарная кластеризация с помощью QUBO

Неправильное назначение кластера.

Хорошее кластерное задание.

Визуальное представление задачи кластеризации с 20 точками: круги одного цвета принадлежат одному кластеру. Каждый круг можно понимать как двоичную переменную в соответствующей задаче QUBO.

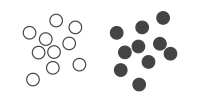
В качестве наглядного примера того, как QUBO можно использовать для кодирования задачи оптимизации, рассмотрим задачу кластерного анализа . Здесь нам дан набор из 20 точек в 2D-пространстве, описываемый матрицей $D\in \mathbb {R} ^{20\times 2}$, где каждая строка содержит две декартовых координаты . Мы хотим присвоить каждую точку одному из двух классов или кластеров , чтобы точки в одном кластере были похожи друг на друга. Для двух кластеров мы можем назначить двоичную переменную $x_{i}\in \mathbb {B}$ до точки, соответствующей $i$-я строка в $D$, указывающий, принадлежит ли он первому ( $x_{i}=0$) или второй кластер ( $x_{i}=1$). Следовательно, у нас есть 20 бинарных переменных, которые образуют бинарный вектор $x\in \mathbb {B} ^{20}$ что соответствует кластерному назначению всех точек (см. рисунок).

Один из способов получить кластеризацию — рассмотреть попарные расстояния между точками. Учитывая назначение кластера $x$, один из $x_{i}x_{j}$ или $(1-x_{i})(1-x_{j})$ оценивается как 1, если указывает $i$ и $j$ находятся в одном кластере. Аналогично, один из $x_{i}(1-x_{j})$ или $(1-x_{i})x_{j}$ указывает на то, что они находятся в разных кластерах. Позволять $d_{ij}\geq 0$ обозначаем евклидово расстояние между точками $i$ и $j$. Чтобы определить функцию стоимости, которую следует минимизировать, когда точки $i$ и $j$ находятся в одном кластере, мы добавляем их положительное расстояние $d_{ij}$и вычтите его, когда они находятся в разных кластерах. Таким образом, оптимальное решение имеет тенденцию помещать точки, находящиеся далеко друг от друга, в разные кластеры, а точки, расположенные близко, — в один и тот же кластер. Таким образом, функция стоимости сводится к

${\begin{aligned}f(x)&=\sum _{i<j}d_{ij}(x_{i}x_{j}+(1-x_{i})(1-x_{j}))-d_{ij}(x_{i}(1-x_{j})+(1-x_{i})x_{j})\\&=\sum _{i<j}\left[4d_{ij}x_{i}x_{j}-2d_{ij}x_{i}-2d_{ij}x_{j}+d_{ij}\right]\end{aligned}}$

Из второй строки параметры QUBO можно легко найти, переставив их следующим образом:

${\begin{aligned}Q_{ij}&={\begin{cases}d_{ij}&{\text{if }}i\neq j\\-\left(\sum \limits _{k=1}^{i-1}d_{ki}+\sum \limits _{\ell =i+1}^{n}d_{i\ell }\right)&{\text{if }}i=j\end{cases}}\end{aligned}}$

Используя эти параметры, оптимальное решение QUBO будет соответствовать оптимальному кластеру относительно функции выше стоимости.

Подключение к моделям Изинга

QUBO очень тесно связан и вычислительно эквивалентен модели Изинга которой , функция Гамильтона определяется как

$H(\sigma )=-\sum _{\langle i~j\rangle }J_{ij}\sigma _{i}\sigma _{j}-\mu \sum _{j}h_{j}\sigma _{j}$

с вещественными параметрами $h_{j},J_{ij},\mu$ для всех $i,j$. Спиновые переменные $\sigma _{j}$ являются двоичными со значениями из $\lbrace -1,+1\rbrace$ вместо $\mathbb {B}$. Более того, в модели Изинга переменные обычно располагаются в решетке, где только соседние пары переменных $\langle i~j\rangle$ может иметь ненулевые коэффициенты. Применение идентичности $\sigma \mapsto 2x-1$ дает эквивалентную задачу QUBO:

${\begin{aligned}f(x)&=\sum _{\langle i~j\rangle }-J_{ij}(2x_{i}-1)(2x_{j}-1)+\sum _{j}\mu h_{j}(2x_{j}-1)\\&=\sum _{\langle i~j\rangle }(-4J_{ij}x_{i}x_{j}+2J_{ij}x_{i}+2J_{ij}x_{j}-J_{ij})+\sum _{j}(2\mu h_{j}x_{j}-\mu h_{j})&&{\text{using }}x_{j}=x_{j}x_{j}\\&=\sum _{\langle i~j\rangle }(-4J_{ij}x_{i}x_{j})+\sum _{\langle i~j\rangle }2J_{ij}x_{i}+\sum _{\langle i~j\rangle }2J_{ij}x_{j}+\sum _{j}2\mu h_{j}x_{j}-\sum _{\langle i~j\rangle }J_{ij}-\sum _{j}\mu h_{j}\\&=\sum _{\langle i~j\rangle }(-4J_{ij}x_{i}x_{j})+\sum _{\langle j~i\rangle }2J_{ji}x_{j}+\sum _{\langle i~j\rangle }2J_{ij}x_{j}+\sum _{j}2\mu h_{j}x_{j}-\sum _{\langle i~j\rangle }J_{ij}-\sum _{j}\mu h_{j}&&{\text{using }}\sum _{\langle i~j\rangle }=\sum _{\langle j~i\rangle }\\&=\sum _{\langle i~j\rangle }(-4J_{ij}x_{i}x_{j})+\sum _{j}\sum _{\langle k=j~i\rangle }2J_{ki}x_{j}+\sum _{j}\sum _{\langle i~k=j\rangle }2J_{ik}x_{j}+\sum _{j}2\mu h_{j}x_{j}-\sum _{\langle i~j\rangle }J_{ij}-\sum _{j}\mu h_{j}\\&=\sum _{\langle i~j\rangle }(-4J_{ij}x_{i}x_{j})+\sum _{j}\left(\sum _{\langle i~k=j\rangle }(2J_{ki}+2J_{ik})+2\mu h_{j}\right)x_{j}-\sum _{\langle i~j\rangle }J_{ij}-\sum _{j}\mu h_{j}&&{\text{using }}\sum _{\langle k=j~i\rangle }=\sum _{\langle i~k=j\rangle }\\&=\sum _{i=1}^{n}\sum _{j=1}^{i}Q_{ij}x_{i}x_{j}+C\end{aligned}}$

где

${\begin{aligned}Q_{ij}&={\begin{cases}-4J_{ij}&{\text{if }}i\neq j\\\sum _{\langle i~k=j\rangle }(2J_{ki}+2J_{ik})+2\mu h_{j}&{\text{if }}i=j\end{cases}}\\C&=-\sum _{\langle i~j\rangle }J_{ij}-\sum _{j}\mu h_{j}\end{aligned}}$

и используя тот факт, что для двоичной переменной $x_{j}=x_{j}x_{j}$.

Поскольку константа $C$ не меняет положения оптимума $x^{*}$, им можно пренебречь при оптимизации, и он важен только для восстановления исходного значения функции Гамильтона.

Внешние ссылки

• QUBO Benchmark (Бенчмарк пакетов программного обеспечения для точного решения QUBO; часть известной коллекции тестов Mittelmann)

• Эндре Борос, Питер Л. Хаммер и Габриэль Таварес (апрель 2007 г.). «Эвристика локального поиска для квадратичной неограниченной двоичной оптимизации (QUBO)» . Журнал эвристики . 13 (2). Ассоциация вычислительной техники: 99–132. дои : 10.1007/s10732-007-9009-3 . S2CID   32887708 . Проверено 12 мая 2013 г.
• Ди Ван и Роберт Кляйнберг (ноябрь 2009 г.). «Анализ задач квадратичной неограниченной бинарной оптимизации с помощью многопродуктовых потоков» . Дискретная прикладная математика . 157 (18). Эльзевир: 3746–3753. дои : 10.1016/j.dam.2009.07.009 . ПМК   2808708 . ПМИД   20161596 .