Графическая модель

Графическая модель или вероятностная графическая модель ( ПГМ ) или структурированная вероятностная модель — это вероятностная модель , для которой граф выражает структуру условной зависимости между случайными величинами . Они обычно используются в теории вероятностей , статистике (особенно байесовской статистике ) и машинном обучении .

Виды графических моделей

Как правило, вероятностные графические модели используют представление на основе графов в качестве основы для кодирования распределения в многомерном пространстве и граф, который представляет собой компактное или факторизованное представление набора зависимостей, которые выполняются в конкретном распределении. Обычно используются две ветви графического представления распределений, а именно байесовские сети и марковские случайные поля . Оба семейства включают в себя свойства факторизации и независимости, но они различаются набором независимости, которую они могут кодировать, и факторизацией распределения, которую они вызывают. ^[1]

Неориентированная графическая модель

Показанный неориентированный граф может иметь одну из нескольких интерпретаций; общей чертой является то, что наличие ребра подразумевает некоторую зависимость между соответствующими случайными величинами. Из этого графика мы можем сделать вывод, что $B,C,D$ все взаимно независимы, однажды $A$ известно, или (что эквивалентно в данном случае), что

P[A,B,C,D]=f_{AB}[A,B]\cdot f_{AC}[A,C]\cdot f_{AD}[A,D]

для некоторых неотрицательных функций $f_{AB},f_{AC},f_{AD}$ .

Байесовская сеть

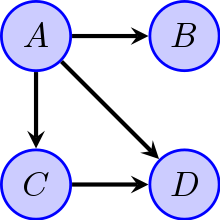
Если сетевая структура модели представляет собой ориентированный ациклический граф , модель представляет собой факторизацию совместной вероятности всех случайных величин. Точнее, если события $X_{1},\ldots ,X_{n}$ тогда совместная вероятность удовлетворяет

P[X_{1},\ldots ,X_{n}]=\prod _{i=1}^{n}P[X_{i}|{\text{pa}}(X_{i})]

где ${\text{pa}}(X_{i})$ это набор родителей узла $X_{i}$ (узлы с ребрами, направленными в сторону $X_{i}$ ). Другими словами, совместное распределение факторов превращается в продукт условных распределений. Например, в ориентированном ациклическом графе, показанном на рисунке, эта факторизация будет иметь вид

P[A,B,C,D]=P[A]\cdot P[B|A]\cdot P[C|A]\cdot P[D|A,C]

.

Любые два узла условно независимы, учитывая значения их родителей. критерий, называемый d -разделением В общем, любые два набора узлов условно независимы с учетом третьего набора, если в графе выполняется . Локальная независимость и глобальная независимость эквивалентны в байесовских сетях.

Этот тип графической модели известен как направленная графическая модель, байесовская сеть или сеть убеждений. Классические модели машинного обучения, такие как скрытые модели Маркова , нейронные сети и новые модели, такие как модели Маркова переменного порядка, можно считать частными случаями байесовских сетей.

Одной из простейших байесовских сетей является наивный байесовский классификатор .

Циклические направленные графические модели

На следующем рисунке изображена графическая модель с циклом. Это можно интерпретировать в терминах того, что каждая переменная каким-то образом «зависит» от значений ее родителей. Конкретный показанный график предполагает совместную плотность вероятности, которая учитывается как

P[A,B,C,D]=P[A]\cdot P[B]\cdot P[C,D|A,B]

,

но возможны и другие интерпретации. ^[2]

Другие типы

Сеть зависимостей , где циклы разрешены
Древовидный классификатор или модель TAN

Целевое байесовское сетевое обучение (TBNL)
Модель TBNL для «набора данных загона»
Факторный граф — это неориентированный двудольный граф, соединяющий переменные и факторы. Каждый фактор представляет собой функцию над переменными, с которыми он связан. Это полезное представление для понимания и реализации распространения убеждений .
Дерево клик или дерево соединений — это , используемое дерево клик в алгоритме дерева соединений .
Цепной граф — это граф, который может иметь как направленные, так и ненаправленные ребра, но без каких-либо направленных циклов (т.е. если мы начинаем с любой вершины и двигаемся по графу, соблюдая направления любых стрелок, мы не можем вернуться к вершине, с которой начали, если мы прошли стрелку). Как ориентированные ациклические графы, так и неориентированные графы являются частными случаями цепных графов, которые, следовательно, могут обеспечить способ объединения и обобщения байесовских и марковских сетей. ^[3]
— Родовой граф это дальнейшее расширение, имеющее направленные, двунаправленные и неориентированные ребра. ^[4]
случайного поля Методы
- Марковское случайное поле , также известное как марковская сеть, представляет собой модель неориентированного графа . Графическая модель со многими повторяющимися субъединицами может быть представлена табличными обозначениями .
- Условное случайное поле — это дискриминативная модель, заданная на неориентированном графе.
Ограниченная машина Больцмана — это двудольная генеративная модель, заданная на неориентированном графе.

Приложения

Структура моделей, которая предоставляет алгоритмы обнаружения и анализа структуры в сложных распределениях для их краткого описания и извлечения неструктурированной информации, позволяет их эффективно конструировать и использовать. ^[1] Приложения графических моделей включают причинный вывод , извлечение информации , распознавание речи , компьютерное зрение , декодирование кодов проверки четности низкой плотности , моделирование генных регуляторных сетей , поиск генов и диагностику заболеваний, а также графические модели структуры белков .

См. также

Примечания

^ Перейти обратно: ^а ^б Коллер, Д .; Фридман, Н. (2009). Вероятностные графические модели . Массачусетс: MIT Press. п. 1208. ИСБН 978-0-262-01319-2 . Архивировано из оригинала 27 апреля 2014 г.
^ Ричардсон, Томас (1996). «Алгоритм открытия ориентированных циклических графов». Материалы двенадцатой конференции по неопределенности в искусственном интеллекте . ISBN 978-1-55860-412-4 .
^ Фриденберг, Мортен (1990). «Свойство Маркова цепного графа». Скандинавский статистический журнал . 17 (4): 333–353. JSTOR 4616181 . МР 1096723 .
^ Ричардсон, Томас; Спиртес, Питер (2002). «Марковские модели наследственного графа». Анналы статистики . 30 (4): 962–1030. CiteSeerX 10.1.1.33.4906 . дои : 10.1214/aos/1031689015 . МР 1926166 . Збл 1033.60008 .

Дальнейшее чтение

Книги и главы книг

Барбер, Дэвид (2012). Байесовское рассуждение и машинное обучение . Издательство Кембриджского университета. ISBN 978-0-521-51814-7 .

Бишоп, Кристофер М. (2006). «Глава 8. Графические модели» (PDF) . Распознавание образов и машинное обучение . Спрингер. стр. 359–422. ISBN 978-0-387-31073-2 . МР 2247587 .
Коуэлл, Роберт Г.; Дэвид, А. Филип ; Лауритцен, Штеффен Л.; Шпигельхальтер, Дэвид Дж. (1999). Вероятностные сети и экспертные системы . Берлин: Шпрингер. ISBN 978-0-387-98767-5 . МР 1697175 . Более продвинутая и статистически ориентированная книга.
Дженсен, Финн (1996). Введение в байесовские сети . Берлин: Шпрингер. ISBN 978-0-387-91502-9 .
Перл, Иудея (1988). Вероятностное рассуждение в интеллектуальных системах (2-е исправленное изд.). Сан-Матео, Калифорния: Морган Кауфманн . ISBN 978-1-55860-479-7 . МР 0965765 . Подход вычислительного рассуждения, при котором формально вводятся взаимосвязи между графиками и вероятностями.

Журнальные статьи

Эдоардо М. Айрольди (2007). «Начало работы с вероятностными графическими моделями» . PLOS Вычислительная биология . 3 (12): е252. arXiv : 0706.2040 . Бибкод : 2007PLSCB...3..252A . дои : 10.1371/journal.pcbi.0030252 . ПМК 2134967 . ПМИД 18069887 .
Джордан, Мичиган (2004). «Графические модели» . Статистическая наука . 19 : 140–155. дои : 10.1214/088342304000000026 .
Гахрамани, Зубин (май 2015 г.). «Вероятностное машинное обучение и искусственный интеллект» . Природа . 521 (7553): 452–459. Бибкод : 2015Natur.521..452G . дои : 10.1038/nature14541 . ПМИД 26017444 . S2CID 216356 .

Другой

Внешние ссылки

[koller09-1] Перейти обратно: ^а ^б Коллер, Д .; Фридман, Н. (2009). Вероятностные графические модели . Массачусетс: MIT Press. п. 1208. ИСБН 978-0-262-01319-2 . Архивировано из оригинала 27 апреля 2014 г.

[richardson95causal-2] Ричардсон, Томас (1996). «Алгоритм открытия ориентированных циклических графов». Материалы двенадцатой конференции по неопределенности в искусственном интеллекте . ISBN 978-1-55860-412-4 .

[3] Фриденберг, Мортен (1990). «Свойство Маркова цепного графа». Скандинавский статистический журнал . 17 (4): 333–353. JSTOR 4616181 . МР 1096723 .

[4] Ричардсон, Томас; Спиртес, Питер (2002). «Марковские модели наследственного графа». Анналы статистики . 30 (4): 962–1030. CiteSeerX 10.1.1.33.4906 . дои : 10.1214/aos/1031689015 . МР 1926166 . Збл 1033.60008 .

[1]

[2]

[3]

[4]