Перспективность

Для более широкого освещения этой темы см. Перспектива (геометрия) .

В геометрии и в ее приложениях к рисованию перспектива — это формирование изображения в картинной плоскости сцены, наблюдаемой из фиксированной точки.

Графика

Наука о графической перспективе использует перспективы для создания реалистичных изображений в правильных пропорциях. По словам Кирсти Андерсен , первым автором, описавшим перспективу, был Леон Альберти в его «De Pictura » (1435). На английском языке Брук Тейлор представил свою «Линейную перспективу» в 1715 году, где объяснил: «Перспектива — это искусство рисовать на плоскости внешний вид любых фигур по правилам геометрии». Во второй книге « Новые принципы линейной перспективы» (1719 г.) Тейлор написал:

Когда линии, проведенные по определенному закону из нескольких частей какой-либо фигуры, разрезают плоскость и посредством этого разреза или пересечения описывают фигуру на этой плоскости, эта фигура, описанная таким образом, называется проекцией другой фигуры. Линии, создающие эту Проекцию, вместе взятые, называются Системой Лучей . И когда все эти Лучи проходят через одну и ту же Точку, они называются Конусом Лучей . И когда эту Точку рассматривают как Глаз Зрителя, эта Система Лучей называется Оптическим Конусом.

Проективная геометрия

Перспектива:
$ABCD\doublebarwedge A'B'C'D',$

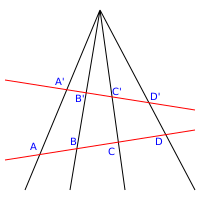
В проективной геометрии точки прямой называются проективным образцом , а совокупность прямых на плоскости, относящихся к точке, называется карандашом .

Учитывая две строки $\ell$ и $m$ в проективной плоскости и точка P этой плоскости ни на одной из прямых, биективное отображение между точками диапазона $\ell$ и диапазон $m$ определяемая линиями карандаша на P, называется перспективой (точнее, центральной перспективой с центром P ). Специальный символ использовался, чтобы показать, что точки X и Y связаны перспективой; $X\doublebarwedge Y.$ В этих обозначениях, чтобы показать, что центром перспективы является P , напишите $X\ {\overset {P}{\doublebarwedge }}\ Y.$

Существование перспективы означает, что соответствующие точки находятся в перспективе . Двойственная , представляет собой соответствие между линиями двух карандашей , концепция, осевая перспектива определяемое проективным диапазоном.

Проективность

Основная статья: Проективность

Композиция двух перспектив вообще не является перспективой. Перспективность или композиция двух и более перспектив называется проективностью ( проективная трансформация , проективная коллинеация и гомография — синонимы ).

Есть несколько результатов, касающихся проективностей и перспектив, которые справедливы в любой папповской проективной плоскости:

Теорема: Любая проективность между двумя различными проективными диапазонами может быть записана как композиция не более чем двух перспектив.

Теорема: Любую проективность из проективного диапазона в себя можно записать как композицию трех перспектив.

Теорема: Проективность между двумя различными проективными диапазонами, фиксирующая точку, является перспективой.

Многомерные

Биективное соответствие между точками на двух прямых на плоскости, определяемое точкой этой плоскости, не лежащей ни на одной прямой, имеет аналоги более высокой размерности, которые также будут называться перспективами.

Пусть Sm _{мерных проективных пространства ,} и Tm _— два различных - содержащихся в n -мерном проективном пространстве Rn _. m Пусть P _{n − m −1} — ( n − m − 1)-мерное подпространство R _n, не имеющее общих точек ни с S _m, ни с T _m . Для каждой точки из Sm пространство _в L, натянутое на и Pn - _{m , - 1} пересекает Tm _Y точке X = fP _X ( X ) . Это соответствие f _P также называется перспективой. Описанная выше центральная перспектива имеет место при n = 2 и m = 1 .

Перспективные коллинеации

Пусть S ₂ и T ₂ — две различные проективные плоскости в проективном 3-пространстве R ₃ . Поскольку O и O * не являются точками R ₃ ни в одной из плоскостей, используйте конструкцию последнего раздела для проецирования S ₂ на T ₂ с помощью перспективы с центром O, за которой следует проекция T ₂ обратно на S ₂ с перспективой с центром. О *. Эта композиция представляет собой биективное отображение точек S ₂ на себя, которое сохраняет коллинеарные точки и называется перспективной коллинеацией ( центральной коллинеацией в более современной терминологии). Пусть φ — перспективная коллинеация S ₂ . Каждая точка линии пересечения S ₂ и T ₂ будет зафиксирована φ и эта линия называется осью φ. Пусть точка Р будет пересечением прямой ОО плоскостью S2 _{* с} . P также фиксируется φ, и каждая линия S2 _, проходящая через P, стабилизируется φ (фиксированной, но не обязательно поточечно фиксированной). P называется центром φ. Ограничение φ на любую линию S2 _, не проходящую через P, центральной перспективой в S2 _{является} с центром P между этой линией и линией, которая является ее образом под φ.

См. также

• Перспективная проекция
• Теорема Дезарга

Примечания

Жан Дю Брей , Различные универсальные и новые методы, полностью или частично, для создания перспектив , 1642 г.

Ссылки

• Андерсен, Кирсти (1992), Работа Брука Тейлора о линейной перспективе , Springer, ISBN  0-387-97486-5
• Коксетер, Гарольд Скотт Макдональд (1969), Введение в геометрию (2-е изд.), Нью-Йорк: John Wiley & Sons , ISBN  978-0-471-50458-0 , МР   0123930
• Фишбэк, WT (1969), Проективная и евклидова геометрия , John Wiley & Sons
• Педо, Дэн (1988), Геометрия / Комплексный курс , Дувр, ISBN  0-486-65812-0
• Янг, Джон Уэсли (1930), Проективная геометрия , Математические монографии Каруса (№ 4), Математическая ассоциация Америки

Внешние ссылки

• Кристофер Купер Перспективы и проективности .
• Джеймс К. Морхед-младший (1911) Перспективная и проективная геометрия: сравнение, Университет Райса .
• Джона Тейлора Проективная геометрия из Брайтонского университета .