Медоид

Медоиды — это репрезентативные объекты набора данных или кластера внутри набора данных, сумма различий которых со всеми объектами в кластере минимальна. Медоиды по своей концепции аналогичны средним или центроидам , но медоиды всегда могут быть членами набора данных. Медоиды чаще всего используются для данных, когда среднее значение или центроид невозможно определить, например, для графиков. Они также используются в контекстах, где центроид не является репрезентативным для набора данных, например, в изображениях, трехмерных траекториях и экспрессии генов. (где, хотя данных мало, медоид может не присутствовать). Они также представляют интерес при поиске представителя с использованием некоторого расстояния, отличного от квадрата евклидова расстояния (например, в рейтингах фильмов).

Для некоторых наборов данных может быть более одного медоида, как в случае с медианами. Распространенным применением медоида является алгоритм кластеризации k-medoids , который аналогичен алгоритму k-means , но работает, когда среднее значение или центроид невозможно определить. Этот алгоритм в основном работает следующим образом. Сначала случайным образом выбирается набор медоидов. Во-вторых, вычисляются расстояния до других точек. В-третьих, данные кластеризуются в соответствии с медоидом, на который они наиболее похожи. В-четвертых, набор медоидов оптимизируется посредством итерационного процесса.

Обратите внимание, что медоид не эквивалентен медиане , геометрической медиане или центроиду . Медиана нормой определяется только для одномерных данных и минимизирует только отличие от других точек для метрик, вызванных ( например, Манхэттенское расстояние или Евклидово расстояние ). Геометрическая медиана определяется в любом измерении, но в отличие от медоида она не обязательно является точкой исходного набора данных.

Определение

Позволять ${\textstyle {\mathcal {X}}:=\{x_{1},x_{2},\dots ,x_{n}\}}$ быть набором ${\textstyle n}$ точки в пространстве с функцией расстояния d. Медоид определяется как

$x_{\text{medoid}}=\arg \min _{y\in {\mathcal {X}}}\sum _{i=1}^{n}d(y,x_{i}).$

Кластеризация с помощью медоидов

Основная статья: к-медоиды

Медоиды являются популярной заменой кластерного среднего, когда функция расстояния не является (возведенной в квадрат) евклидовым расстоянием или даже не является метрикой ( поскольку медоид не требует неравенства треугольника). При разбиении набора данных на кластеры медоид каждого кластера можно использовать в качестве представителя каждого кластера.

Алгоритмы кластеризации, основанные на идее медоидов, включают:

• Разделение вокруг медоидов (PAM), стандартный k-medoids. алгоритм
• Иерархическая кластеризация вокруг медоидов (HACAM), которая использует медоиды в иерархической кластеризации.

Алгоритмы вычисления медоида множества

Из определения, приведенного выше, ясно, что медоид множества ${\mathcal {X}}$ может быть вычислено после вычисления всех попарных расстояний между точками ансамбля. Это потребует ${\textstyle O(n^{2})}$ дистанционные оценки (с $n=|{\mathcal {X}}|$). В худшем случае невозможно вычислить медоид с меньшим количеством оценок расстояния. Однако существует множество подходов, которые позволяют нам вычислять медоиды точно или приблизительно за субквадратичное время в рамках различных статистических моделей.

Если точки лежат на реальной линии, вычисление медоида сводится к вычислению медианы, что можно сделать в ${\textstyle O(n)}$ по алгоритму быстрого выбора Хоара. Однако в реальных пространствах более высоких размерностей алгоритм линейного времени неизвестен. РЭНД — это алгоритм, который оценивает среднее расстояние каждой точки до всех остальных точек путем выборки случайного подмножества других точек. Всего требуется ${\textstyle O\left({\frac {n\log n}{\epsilon ^{2}}}\right)}$ вычисления расстояний для аппроксимации медоида с точностью до коэффициента ${\textstyle (1+\epsilon \Delta )}$ с большой вероятностью, где ${\textstyle \Delta }$ это максимальное расстояние между двумя точками в ансамбле. Обратите внимание, что RAND — это аппроксимационный алгоритм, причем ${\textstyle \Delta }$ может быть не известно априори.

RAND использовала ТОПРАНК который использует оценки, полученные с помощью RAND оценивает среднее расстояние этих точек , чтобы сосредоточиться на небольшом подмножестве точек-кандидатов, точно и выбирает минимальное из них. ТОПРАНК нуждается ${\textstyle O(n^{\frac {5}{3}}\log ^{\frac {4}{3}}n)}$ расчеты расстояний найти точный медоид с высокой вероятностью согласно предположению о распределении на средних дистанциях.

обрезанный представляет алгоритм найти медоид с помощью ${\textstyle O(n^{\frac {3}{2}}2^{\Theta (d)})}$ дистанционные оценки в рамках распределительного предположение по пунктам. Алгоритм использует неравенство треугольника для сокращения пространства поиска.

Вы сказали рычаги воздействия связь вычислений медоида с многорукими бандитами и использует алгоритм с верхней границей достоверности, чтобы получить алгоритм, который принимает ${\textstyle O(n\log n)}$ дистанционные оценки в рамках статистических предположения по пунктам.

Коррелированное последовательное сокращение вдвое также использует методы многорукого бандита, улучшая Meddit . Используя корреляционную структуру задачи, алгоритм способен значительно улучшить (обычно примерно на 1-2 порядка) как количество необходимых вычислений расстояния, так и время настенных часов.

Реализации

Реализацию RAND , TOPRANK и Trimed можно найти здесь . Реализация Меддит можно найти здесь и здесь . Реализация коррелированного последовательного халвинга можно найти здесь .

Медоиды в обработке текста и естественного языка (НЛП)

Медоиды можно применять к различным текстовым задачам и задачам НЛП для повышения эффективности и точности анализа. Кластеризуя текстовые данные на основе сходства, медоиды могут помочь идентифицировать репрезентативные примеры в наборе данных, что приводит к лучшему пониманию и интерпретации данных.

Кластеризация текста

Кластеризация текста — это процесс группировки схожего текста или документов на основе их содержания. Алгоритмы кластеризации на основе Medoid можно использовать для разделения больших объемов текста на кластеры, где каждый кластер представлен документом medoid. Этот метод помогает организовывать, обобщать и извлекать информацию из больших коллекций документов, например, в поисковых системах, аналитике социальных сетей и системах рекомендаций.

Обобщение текста

Целью резюмирования текста является создание краткого и связного изложения более крупного текста путем извлечения наиболее важной и актуальной информации. Кластеризация на основе Medoid может использоваться для выявления наиболее репрезентативных предложений в документе или группе документов, которые затем можно объединить для создания резюме. Этот подход особенно полезен для задач экстрактивного реферирования, целью которых является создание резюме путем выбора наиболее релевантных предложений из исходного текста.

Анализ настроений

Анализ настроений включает в себя определение настроения или эмоции, выраженной в фрагменте текста, например положительного, отрицательного или нейтрального. Кластеризация на основе Medoid может применяться к групповым текстовым данным на основе схожих шаблонов настроений. Анализируя медоид каждого кластера, исследователи могут получить представление о преобладающих настроениях в кластере, помогая в таких задачах, как сбор мнений, анализ отзывов клиентов и мониторинг социальных сетей.

Тематическое моделирование

Тематическое моделирование — это метод, используемый для обнаружения абстрактных тем, встречающихся в коллекции документов. Кластеризация на основе Medoid может применяться к групповым документам со схожими темами или темами. Анализируя медоиды этих кластеров, исследователи могут понять основные темы в текстовом корпусе, облегчая такие задачи, как категоризация документов, анализ тенденций и рекомендации по содержанию.

Методы измерения сходства текста при кластеризации на основе медоидов

При применении кластеризации на основе медоидов к текстовым данным важно выбрать соответствующую меру сходства для эффективного сравнения документов. Каждый метод имеет свои преимущества и ограничения, и выбор меры сходства должен основываться на конкретных требованиях и характеристиках анализируемых текстовых данных. Ниже приведены распространенные методы измерения сходства текста при кластеризации на основе медоидов:

В этом примере показано, как косинусное сходство будет сравнивать угол линий между объектами, чтобы определить, насколько они похожи. Обратите внимание, что большинство вложений текста будут иметь как минимум несколько сотен измерений вместо двух.

Косинусное подобие

Косинусное сходство — широко используемый показатель для сравнения сходства между двумя частями текста. Он вычисляет косинус угла между двумя векторами документа в многомерном пространстве. Косинусное сходство находится в диапазоне от -1 до 1, где значение ближе к 1 указывает на большее сходство, а значение ближе к -1 указывает на меньшее сходство. Визуализируя две линии, исходящие из начала координат и идущие к соответствующим точкам интереса, а затем измеряя угол между этими линиями, можно определить сходство между связанными точками. На косинусное сходство меньше влияет длина документа, поэтому может быть лучше создавать медоиды, которые представляют содержимое кластера, а не длину.

Сходство Жаккара

Эту формулу подобия Жаккара можно легко применить к тексту.

Сходство Жаккара, также известное как коэффициент Жаккара, измеряет сходство между двумя множествами путем сравнения отношения их пересечения к их объединению. В контексте текстовых данных каждый документ представлен как набор слов, а сходство Жаккара вычисляется на основе общих слов между двумя наборами. Сходство Жаккара находится в диапазоне от 0 до 1, где более высокое значение указывает на более высокую степень сходства между документами.

Евклидово расстояние

В этом примере показано, как евклидово расстояние рассчитывает расстояние между объектами, чтобы определить, насколько они похожи. Обратите внимание, что большинство вложений текста будут иметь как минимум несколько сотен измерений вместо двух.

Евклидово расстояние — это стандартная метрика расстояния, используемая для измерения несходства между двумя точками в многомерном пространстве. В контексте текстовых данных документы часто представляются в виде многомерных векторов, таких как векторы TF, и евклидово расстояние может использоваться для измерения несходства между ними. Меньшее евклидово расстояние указывает на более высокую степень сходства между документами. Использование евклидова расстояния может привести к тому, что медоиды будут более точно отражать длину документа.

Изменить расстояние

Расстояние редактирования, также известное как расстояние Левенштейна, измеряет сходство между двумя строками путем расчета минимального количества операций (вставок, удалений или замен), необходимых для преобразования одной строки в другую. В контексте текстовых данных расстояние редактирования можно использовать для сравнения сходства между короткими текстовыми документами или отдельными словами. Меньшее расстояние редактирования указывает на более высокую степень сходства между строками.

Приложения Medoid в больших языковых моделях

Медоиды для анализа вложений больших языковых моделей.

Это пример того, как текст может быть сгруппирован с похожими элементами при внедрении на основе местоположения. Это представляет собой группировку по евклидову расстоянию. Если бы они были сгруппированы по другой мере сходства, например по косинусному сходству, то медоиды могли бы быть разными.

Медоиды можно использовать для анализа и понимания представлений векторного пространства, созданных большими языковыми моделями (LLM), такими как BERT, GPT или RoBERTa. Применяя кластеризацию на основе медоидов к вложениям, созданным этими моделями для слов, фраз или предложений, исследователи могут исследовать семантические отношения, фиксируемые LLM. Этот подход может помочь идентифицировать кластеры семантически схожих объектов, обеспечивая понимание структуры и организации многомерных пространств внедрения, созданных этими моделями.

Медоиды для отбора данных и активного обучения

Активное обучение включает в себя выбор точек данных из обучающего пула, которые позволят максимизировать производительность модели. Медоиды могут сыграть решающую роль в выборе данных и активном обучении с помощью LLM. Кластеризация на основе Medoid может использоваться для идентификации репрезентативных и разнообразных выборок из большого набора текстовых данных, которые затем можно использовать для более эффективной настройки LLM или для создания лучших обучающих наборов. Выбирая медоиды в качестве обучающих примеров, исследователи могут получить более сбалансированный и информативный обучающий набор, что потенциально улучшит обобщение и надежность точно настроенных моделей.

Медоиды для интерпретируемости модели и безопасности

Применение медоидов в контексте LLM может способствовать улучшению интерпретируемости модели. Кластеризуя вложения, генерируемые LLM, и выбирая медоидов в качестве представителей каждого кластера, исследователи могут предоставить более интерпретируемую сводку поведения модели. Этот подход может помочь понять процесс принятия решений в модели, выявить потенциальные отклонения и раскрыть основную структуру вложений, генерируемых LLM. Поскольку дискуссия вокруг интерпретируемости и безопасности LLM продолжает набирать обороты, использование медоидов может служить ценным инструментом для достижения этой цели.

Реальные приложения

Как универсальный метод кластеризации, медоиды можно применять для решения множества реальных проблем во многих областях, от биологии и медицины до рекламы и маркетинга, а также социальных сетей. Его способность обрабатывать сложные наборы данных с высокой степенью сложности делает его мощным устройством в современном анализе данных.

Анализ экспрессии генов

При анализе экспрессии генов Исследователи используют передовые технологии, включающие микрочипы и секвенирование РНК, для измерения уровней экспрессии многочисленных генов в биологических образцах, что приводит к получению многомерных данных, которые могут быть сложными и трудными для анализа. Медоиды являются потенциальным решением, позволяющим группировать гены в первую очередь на основе их профилей экспрессии, что позволяет исследователям обнаруживать совместно экспрессируемые группы генов, которые могут дать ценную информацию о молекулярных механизмах биологических процессов и заболеваний.

Анализ социальных сетей

Для оценки социальной сети, medoids может быть исключительным инструментом для распознавания центральных или влиятельных узлов в социальной сети. Исследователи могут группировать узлы на основе их стилей подключения и определять узлы, которые с наибольшей вероятностью окажут существенное влияние на функционирование и структуру сети. Один из популярных подходов к использованию медоидов в анализе социальных сетей — вычисление показателя расстояния или сходства между парами узлов на основе их свойств.

Сегментация рынка

Медоиды также можно использовать для сегментации рынка. Это аналитическая процедура, включающая группировку клиентов в первую очередь на основе их покупательского поведения, демографических характеристик и различных других признаков. Кластеризация клиентов по сегментам с использованием медоидов позволяет компаниям адаптировать свои методы рекламы и маркетинга таким образом, чтобы они соответствовали потребностям каждой группы клиентов. Медоиды служат репрезентативными факторами внутри каждого кластера, инкапсулируя основные характеристики клиентов в этой группе.

Сумма квадратов ошибок внутри групп (WGSS) — это формула, используемая при сегментации рынка и направленная на количественную оценку концентрации квадратов ошибок внутри кластеров. Он стремится уловить распределение ошибок внутри групп, возводя их в квадрат и агрегируя результаты. Метрика WGSS количественно определяет связность выборок внутри кластеров, указывая на более плотные кластеры с более низкими значениями WGSS и, соответственно, более высокий эффект кластеризации. Формула WGSS:

$${\text{WGSS}}={\frac {1}{2}}\left[(m_{1}-1){\overline {d_{1}^{2}}}+\cdots +(m_{k}-1){\overline {d_{k}^{2}}}\right]$$

Где ${\overline {d_{1}^{2}}}$ — среднее расстояние образцов внутри k -го кластера и $m_{k}$ — количество выборок в k -м кластере.

Обнаружение аномалий

Медоиды также могут сыграть важную роль в выявлении аномалий, и одним из эффективных методов является обнаружение аномалий на основе кластеров. Их можно использовать для обнаружения кластеров точек данных, которые значительно отличаются от остальных данных. Кластеризируя данные в группы с использованием медоидов и сравнивая свойства каждого кластера с данными, исследователи могут четко обнаружить аномальные кластеры.

Визуализация процесса кластеризации на основе медоидов

Цель

Визуализация кластеризации на основе медоидов может быть полезна при попытке понять, как работает кластеризация на основе медоидов. Исследования показали, что люди лучше учатся, используя визуальную информацию. В кластеризации на основе медоидов медоид является центром кластера. Это отличается от кластеризации k-средних , где центр не является реальной точкой данных, а может находиться между точками данных. Мы используем медоид для группировки «кластеров» данных, который получается путем нахождения элемента с минимальным средним отличием от всех остальных объектов в кластере. Хотя в используемом примере визуализации используется кластеризация k-medoids, визуализацию можно применить и к кластеризации k-средних путем замены среднего различия средним значением используемого набора данных.

Визуализация с использованием одномерных данных

Матрица расстояний

Пример нормализованного графика несходства Жаккара с использованием ядерных профилей. Каждый NP сравнивается с каждым другим NP в таблице, и соответствующее различие вводится в ячейку, соответствующую паре сравниваемых NP. Более высокие цифры указывают на большее несходство, а меньшие цифры указывают на большее сходство. Большинство ярлыков исключено из-за ограничений по размеру. Диагональ отмечена цифрой «0», чтобы не искажать данные.

Для кластеризации на основе медоидов требуется матрица расстояний, которая генерируется с использованием различия Жаккара (которое равно 1 — индекс Жаккара ). Эта матрица расстояний используется для расчета расстояния между двумя точками на одномерном графике. На изображении выше показан пример графика различия Жаккара.

Кластеризация

Шаг 1

Кластеризация на основе Medoid используется для поиска кластеров в наборе данных. Исходный одномерный набор данных, содержащий кластеры, которые необходимо обнаружить, используется для процесса кластеризации на основе медоидов. На изображении ниже в наборе данных имеется двенадцать различных объектов в разных положениях по оси X.

Исходный набор данных, который будет использоваться в этом разделе. Серая точка обозначает объект, который не назначен ни одному кластеру.

Шаг 2

В качестве начальных центров выбираются K случайных точек. Значение, выбранное для K, известно как значение K. На изображении ниже в качестве значения K выбрано 3. Процесс поиска оптимального значения K будет обсуждаться на шаге 7.

Первый выбор центра. Большие точки являются центрами, а цвета разделяют каждый объект по его кластеру.

Шаг 3

Каждому нецентральному объекту присваивается ближайший к нему центр. Это делается с помощью матрицы расстояний. Чем меньше различие, тем ближе точки. На изображении ниже 5 объектов в кластере 1, 3 в кластере 2 и 4 в кластере 3.

Начальные кластеры.

Шаг 4

Новый центр для каждого кластера находится путем нахождения объекта, среднее отличие которого от всех других объектов в кластере минимально. Центр, выбранный на этом этапе, называется медоидом. На изображении ниже показаны результаты выбора медоида.

Медоидный выбор.

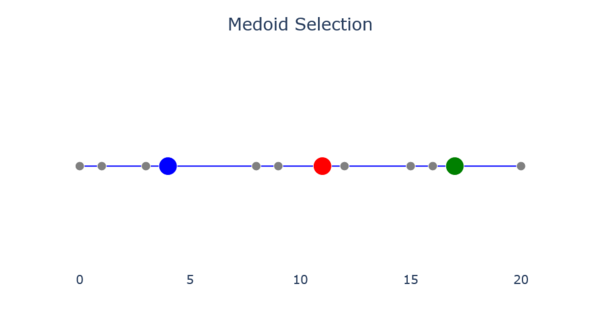
Шаг 5

Шаги 3–4 повторяются до тех пор, пока центры не перестанут двигаться, как на изображениях ниже.

• Повторение шагов 3–4 (слева направо)
• 
  Второй кластер.
• 
  Медоидный выбор.
• 
  Третий кластер.
• 
  Окончательный выбор медоида.

Шаг 6

Окончательные кластеры получаются, когда центры больше не перемещаются между шагами. На изображении ниже показано, как может выглядеть окончательный кластер.

Последние кластеры.

Шаг 7

Вариация суммируется внутри каждого кластера, чтобы увидеть, насколько точны центры. Запустив этот тест с различными значениями K, можно получить « колено » графика вариаций, где вариации графика выравниваются. «Колоко» графика — это оптимальное значение K для набора данных.

Медоиды в больших измерениях

Распространенной проблемой кластеризации k-медоидов и других алгоритмов кластеризации на основе медоидов является « проклятие размерности », при котором точки данных содержат слишком много измерений или признаков. По мере добавления к данным размеров расстояние между ними становится редким. и становится трудно характеризовать кластеризацию только с помощью евклидова расстояния. В результате меры сходства, основанные на расстоянии, сходятся к постоянной величине. и у нас есть характеристика расстояния между точками, которая может не отражать наш набор данных значимым образом.

Одним из способов смягчить последствия проклятия размерности является использование спектральной кластеризации . Спектральная кластеризация обеспечивает более подходящий анализ за счет уменьшения размерности данных с использованием анализа главных компонентов , проецирования точек данных в подпространство меньшей размерности и последующего запуска выбранного алгоритма кластеризации, как и раньше. Однако следует отметить одну вещь: как и при любом уменьшении размерности, мы теряем информацию. поэтому необходимо заранее сопоставить с кластеризацией, насколько необходимо сокращение, прежде чем будет потеряно слишком много данных.

Однако высокая размерность влияет не только на метрики расстояния, поскольку временная сложность также увеличивается с увеличением количества функций. k-medoids чувствителен к первоначальному выбору медоидов, поскольку они обычно выбираются случайным образом. В зависимости от того, как инициализируются такие медоиды, k-медоиды могут сходиться к разным локальным оптимумам, что приводит к различным кластерам и показателям качества. это означает, что k-medoids, возможно, придется запускать несколько раз с разными инициализациями, что приводит к гораздо большему времени выполнения. Один из способов уравновесить это — использовать k-medoids++, альтернатива k-medoids, аналогичная ее аналогу k-means, k-means++, которая выбирает начальные медоиды для начала на основе распределения вероятностей, как своего рода «информированная случайность» или обоснованное предположение, если хотите. Если такие медоиды выбираются по этой причине, результатом будет улучшение времени выполнения и повышение производительности кластеризации. Алгоритм k-medoids++ описывается следующим образом:

1. Начальный медоид выбирается случайным образом среди всех пространственных точек.
2. Для каждой пространственной точки 𝑝 вычислите расстояние между 𝑝 и ближайшими медоидами, которое называется D(𝑝), и просуммируйте все расстояния до 𝑆.
3. Следующий медоид определяется с использованием взвешенного распределения вероятностей. В частности, выбирается случайное число 𝑅 между нулем и суммированным расстоянием 𝑆, и соответствующая пространственная точка является следующим медоидом.
4. Шаги (2) и Шаг (3) повторяются до тех пор, пока не будут выбраны 𝑘 медоиды.

Теперь, когда у нас есть соответствующие первые выборки для медоидов, можно запустить нормальную вариацию k-медоидов.

Внешние ссылки

• Видео StatQuest k-means, используемое для наглядности в #Visualization_of_the_medoid-based_clustering_process разделе