Статическое рассеяние света

Статическое рассеяние света - это метод физической химии , который измеряет интенсивность рассеянного света для получения средней молекулярной массы M _W макромолекулы, такой как полимер или белок в растворе. Измерение интенсивности рассеяния на многих углах позволяет вычислять средний квадратный радиус, также вращения радиусом _. называемый Измеряя интенсивность рассеяния для многих образцов различных концентраций, можно рассчитать второй вириальный коэффициент, A ₂ . ^{[ 1 ]}^{[ 2 ]}^{[ 3 ]}^{[ 4 ]}^{[ 5 ]}

Статическое рассеяние света также обычно используется для определения размера суспензий частиц в диапазонах Sub-мкМ и выше-мкм через Lorenz-Mie (см. Scattering Mie ) и Fraunhofer дифракционные дифракционные формализмы , соответственно.

Для экспериментов по статическому рассеянию света высокоинтенсивный монохроматический свет, обычно лазер, запускается в раствор, содержащий макромолекулы. Один или многие детекторы используются для измерения интенсивности рассеяния под одним или многими углами. Угловая зависимость необходима для получения точных измерений как молярной массы, так и размера для всех макромолекул радиуса выше 1–2% от длины волны падающей. Следовательно, одновременные измерения под несколькими углами относительно направления падающего света, известного как многоугловое рассеяние света (MALS) или многоугловое рассеяние лазерного света (торговые центры), обычно рассматриваются как стандартная реализация статического рассеяния света. Дополнительные подробности об истории и теории MALS можно найти в многоугольном рассеянии света .

Чтобы измерить среднюю молекулярную массу непосредственно без калибровки от интенсивности рассеяния света, интенсивность лазера, квантовая эффективность детектора и полное объем рассеяния и угла сплошного детектора должны быть известны. Поскольку это нецелесообразно, все коммерческие инструменты откалиброваны с использованием сильного, известного рассеятеля, такого как толуол , так как отношение Rayleigh толуола и несколько других растворителей измеряли с использованием абсолютного инструмента рассеяния света.

Теория

Для прибора для рассеяния света, состоящего из многих детекторов, размещенных под разными углами, все детекторы должны реагировать одинаково. Обычно детекторы будут иметь немного различную квантовую эффективность , различные добычи и рассматривают разные объемы геометрического рассеяния. В этом случае нормализация детекторов абсолютно необходима. Чтобы нормализовать детекторы, в первую очередь производится измерение чистого растворителя. Затем в растворитель добавляется изотропный рассеятель. Поскольку изотропные рассеятели разбросают ту же интенсивность под любым углом, эффективность и усиление детектора могут быть нормализованы с помощью этой процедуры. Удобно нормализовать все детекторы до детектора угла на 90 °.

$\ N(\theta )={\frac {I_{R}(\theta )-I_{S}(\theta )}{I_{R}(90)-I_{S}(90)}}$

где я _. (90) - интенсивность рассеяния, измеренная для рассеятеля Рэлея с помощью детектора угла 90 °

Наиболее распространенным уравнением для измерения среднего молекулярного массы, M _W , является уравнение ZIMM ^{[ 5 ]} (Правая сторона уравнения Zimm неверно предоставляется в некоторых текстах, как отмечает Hiemenz и Lodge): ^{[ 6 ]}

${\frac {Kc}{\Delta R(\theta ,c)}}={\frac {1}{M_{w}}}\left(1+{\frac {q^{2}R_{g}^{2}}{3}}+O(q^{4})\right)+2A_{2}c+O(c^{2})$

где

$\ K=4\pi ^{2}n_{0}^{2}(dn/dc)^{2}/N_{\text{A}}\lambda ^{4}$

и

$\ \Delta R(\theta ,c)=R_{A}(\theta )-R_{0}(\theta )$

с

$\ R(\theta )={\frac {I_{A}(\theta )n_{0}^{2}}{I_{T}(\theta )n_{T}^{2}}}{\frac {R_{T}}{N(\theta )}}$

и вектор рассеяния для вертикально поляризованного света

$\ q=4\pi n_{0}\sin(\theta /2)/\lambda$

С n ₀ показатель преломления растворителя λ длина волны источника света, n _{a a} a avogadro constant , c концентрация раствора и D n /d c изменение показателя преломления раствора с изменением концентрации. Интенсивность аналита, измеренного под углом, составляет i _a (θ) . В этих уравнениях подписатель A предназначен для аналита (решение), а T - толуол с соотношением Rayleigh толуола, R _T - 1,35 × 10 ⁻⁵ см ⁻¹ для лазера Hene . Как описано выше, радиус вращения, r _G и второй вириальный коэффициент, A ₂ , также рассчитывается по этому уравнению. Увеличение показателя преломления DN/DC характеризует изменение показателя преломления N с концентрацией C и может быть измерено с помощью дифференциального рефрактометра.

График ZIMM построен из двойной экстраполяции до нулевого угла и нулевой концентрации со многих сторон и множества измерений концентрации. В самой простой форме уравнение Zimm сводится к:

$\ Kc/\Delta R(\theta \rightarrow 0,c\rightarrow 0)=1/M_{w}$

Для измерений, сделанных под низким углом и бесконечным разведением с момента p (0) = 1.

Обычно разработано несколько анализов для анализа рассеяния частиц в растворе для получения вышеизложенных физических характеристик частиц. Простой эксперимент по рассеянию статического света влечет за собой среднюю интенсивность образца, которая корректируется для рассеяния растворителя, даст соотношение Рэлея , R в зависимости от угла или вектора волны Q следующим образом:

Анализ данных

Гинье Сюжет

Интенсивность рассеяния может быть построена как функция угла, чтобы дать информацию о R _g, которая может быть просто рассчитана с использованием приближения Гинье следующим образом:

$\ln(\Delta R(\theta ))=1-(R_{g}^{2}/3)q^{2}$

где ln (Δr (θ)) = lnp (θ) также известен как форм -фактор с q = 4πn ₀ sin (θ/2)/λ . Следовательно, график скорректированного отношения Рэлея , ΔR (θ) против греха ²(θ/2) или q ² даст наклон R _G²/3 . Однако это приближение верно только для QR _G <1 . Обратите внимание, что для графика Гинье значение DN/DC и концентрация не требуется.

Короткий забор

График Kratky обычно используется для анализа конформации белков , но может использоваться для анализа случайного ходьбы модели полимеров . Кратский заговор может быть составлен, замышляя грех ²(I/2) dr (i) против греха (i/2) или q ²ΔR (θ) против q .

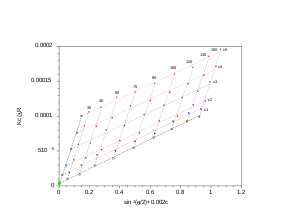
ZIMM Участок

Для полимеров и полимерных комплексов, которые являются монодисперсными ( $\scriptstyle \mu _{2}/{\bar {\Gamma }}^{2}<0.3$ ), как определено статическим рассеянием света, график ZIMM является обычным средством получения параметров, таких как R _G , молекулярная масса M _W и второй вириальный коэффициент A ₂ .

Нужно отметить, что если константа материала не реализована, график ZIMM только даст R _G. K Следовательно, реализация K даст следующее уравнение:

${\frac {Kc}{\Delta R(\theta ,c)}}={\frac {1}{M_{w}}}\left(1+{\frac {q^{2}R_{g}^{2}}{3}}+O(q^{4})\right)+2A_{2}c+O(c^{2})$

Анализ, выполненный с графиком ZIMM, использует двойную экстраполяцию до нулевой концентрации и угол нулевого рассеяния, что приводит к характерному ромбоидному графику. Поскольку угловая информация доступна, также возможно получить радиус вращения ( R _G ). Эксперименты проводятся под несколькими углами, которые удовлетворяют условию $qR_{g}<1$ и по крайней мере 4 концентрации. Выполнение анализа ZIMM на одной концентрации известно как частичный анализ ZIMM и действителен только для разбавленных решений сильных разбросателей точек . Частичный ZIMM , однако, не дает второго вириального коэффициента из -за отсутствия концентрации варианта образца. Более конкретно, что значение второго вириального коэффициента считается либо равным нулем, либо введено в качестве известного значения, чтобы выполнить частичный анализ ZIMM.

Дебай Сюжет

Если измеренные частицы меньше λ/20, форм -фактор P (θ) можно пренебречь ( p (θ) → 1). Следовательно, уравнение Zimm упрощено до уравнения Дебая следующим образом:

${\frac {Kc}{\Delta R(\theta ,c)}}={\frac {1}{M_{w}}}+2A_{2}c$

Обратите внимание, что это также является результатом экстраполяции в нулевой угол рассеяния. Получив данные о концентрации и интенсивности рассеяния, график Debye строится путем построения KC / ΔR (θ) против концентрации. Перехват установленной линии дает молекулярную массу, в то время как наклон соответствует 2 -м вириальному коэффициенту.

Поскольку график Дебая является упрощением уравнения Зимма, применяются те же ограничения последнего, то есть образцы должны представлять монодисперсную природу. Для образцов полидисперса полученная молекулярная масса из статического измерения рассеяния света будет представлять собой среднее значение. Преимущество графика Debye - возможность определить второй вириальный коэффициент. Этот параметр описывает взаимодействие между частицами и растворителем. Например, в растворах макромолекул он может предполагать отрицательные (взаимодействие частиц с частицами частицы предпочтительнее), нулевые или положительные значения (предпочтительнее взаимодействия частиц-растворителя). ^{[ 8 ]}

Множественное рассеяние

Статическое рассеяние света предполагает, что каждый обнаруженный фотон был разбросан только один раз. Следовательно, анализ в соответствии с расчетами, указанными выше, будет правильным только в том случае, если образец был достаточно разбавлен в достаточной степени, чтобы убедиться, что фотоны не разбросаны несколько раз по образцу перед обнаружением. Точная интерпретация становится чрезвычайно сложной для систем с невыплачиваемыми вкладами из множественного рассеяния. Во многих коммерческих инструментах, где анализ сигнала рассеяния автоматически выполняется, пользователь никогда не может быть замечена. В частности, для более крупных частиц и тех, у кого высокий показатель преломления, это ограничивает применение стандартного статического рассеяния света до очень низких концентраций частиц. С другой стороны, для растворимых макромолекул, которые демонстрируют относительно низкий контраст показателя преломления в зависимости от растворителя, включая большинство полимеров и биомолекул в соответствующих растворителях, множественное рассеяние редко является ограничивающим фактором даже при концентрациях, которые приближаются к ограничениям растворимости.

Однако, как показано Шатцелем, ^{[ 9 ]} Можно подавить множественное рассеяние в экспериментах по статическому рассеянию света с помощью кросс-корреляционного подхода. Общая идея состоит в том, чтобы изолировать однократный рассеянный свет и подавить нежелательные вклады от множественного рассеяния в эксперименте по статическому рассеянию света. Были разработаны и применены различные реализации рассеяния кросс-корреляционного света. В настоящее время наиболее широко используемой схемой является так называемый метод 3D-динамического рассеяния света. ^{[ 10 ]}^{[ 11 ]} Тот же метод также может быть использован для коррекции данных динамического рассеяния света для вкладов множественного рассеяния. ^{[ 12 ]}

Статическое рассеяние света-композиции

Образцы, которые изменяют их свойства после разведения, могут не анализироваться с помощью статического рассеяния света с точки зрения простой модели, представленной здесь как уравнение Zimm. известный как «статическое (или многоугольное) рассеяние света» (CG-SLS или CG-MALS), представляет Более сложный анализ , Он дает, в дополнение к размеру и молекулярной массе, информация о сродстве и стехиометрии молекулярных комплексов, образованных одним или несколькими ассоциирующими макромолекулярными/биомолекулярными видами. В частности, статическое рассеяние света из серии разведений может быть проанализировано для количественной оценки самооссофикации, обратимой олигомеризации и неспецифического притяжения или отталкивания, в то время как статическое рассеяние света из смесей видов может быть проанализировано для количественной оценки гетероассоциации. ^{[ 13 ]}

Приложения

Одним из основных применений статического рассеяния света для определения молекулярной массы является в поле макромолекул, таких как белки и полимеры, ^{[ 14 ]}^{[ 15 ]}^{[ 16 ]} поскольку возможно измерить молекулярную массу белков без какого -либо предположения об их форме. Статическое рассеяние света обычно объединяется с другими методами характеристики частиц, такими как хроматография, эксклюзика (SEC), динамическое рассеяние света (DLS) и электрофоретическое рассеяние света (ELS).

Смотрите также

Ссылки

^ А. Эйнштейн (1910). «Теория опалесценции гомогенных жидкостей и жидких смесей вблизи критического состояния» . Анналы физики . 33 (16): 1275. Bibcode : 1910anp ... 338.1275e . Doi : 10.1002/andp.19103381612 .
^ CV Raman (1927). «Соотношение эффекта Тиндалла с осмотическим давлением в коллоидных растворах». Индиан Дж. Физ . 2 : 1.
^ P.Debye (1944). «Световой рассеяние в решениях». J. Appl. Физический 15 (4): 338. Bibcode : 1944jap .... 15..338d . doi : 10.1063/1.1707436 .
^ BH ZIMM (1945). «Молекулярная теория рассеяния света в жидкостях». J. Chem. Физический 13 (4): 141. Bibcode : 1945jchph..13..141z . doi : 10.1063/1.1724013 .
^ Подпрыгнуть до: ^а ^{беременный} BH ZIMM (1948). «Разброс света и радиальное распределение функции высокополимерных растворов». J. Chem. Физический 16 (12): 1093. Bibcode : 1948jchph..16.1093Z . doi : 10.1063/1.1746738 .
^ Iemenz, Paul C.; Лодж, Тимоти П. (2007). Полимер (2 -е изд.). Рот Ратона, Фл. [UU]: CRC Press. стр. 307–308. ISBN 978-1-57444-779-8 .
^ «Измерение молекулярной массы с использованием статического рассеяния света :: Anton Paar Wiki» . Антон Паар . Получено 23 сентября 2022 года .
^ Чанг, Цин (2016), «Осмотическое давление» , коллоидная и графическая химия для контроля качества воды , Elsevier, стр. 37–47, doi : 10.1016/b978-0-12-809315-3.00004-9 , ISBN 978-0-12-809315-3 , Получено 14 июня 2022 года
^ Schaetzel, K. (1991). «Подавление многократного рассеяния с помощью методов кросс-корреляции фотонов». J. MOD Опт . 38 : SA393 - SA398. Bibcode : 1990jpcm .... 2..393s . doi : 10.1088/0953-8984/2/с/062 . S2CID 250745836 .
^ Urban, C.; Schurtenberger, P. (1998). «Характеристика мутных коллоидных суспензий с использованием методов рассеяния света в сочетании с методами кросс-корреляции». J. Colloid Interface Sci . 207 (1): 150–158. Bibcode : 1998JCIS..207..150U . doi : 10.1006/jcis.1998.5769 . PMID 9778402 .
^ Блок, я.; Scheffold, F. (2010). «Модулированное трехмерное рассеяние света поперечного корреляции: улучшение мутной характеристики образца». Обзор научных инструментов . 81 (12): 123107–123107–7. Arxiv : 1008.0615 . BIBCODE : 2010RSCI ... 81L3107B . doi : 10.1063/1.3518961 . PMID 21198014 . S2CID 9240166 .
^ Пьюзи Пн (1999). «Подавление множественного рассеяния с помощью методов кросс-корреляции фотонов». Текущее мнение в области коллоидов и интерфейса . 4 (3): 177–185. doi : 10.1016/s1359-0294 (99) 00036-9 .
^ Некоторые, Д. (2013). «Световой рассеянный анализ биомолекулярных взаимодействий» . Биофиз. Преподобный 5 (2): 147–158. doi : 10.1007/s12551-013-0107-1 . PMC 3641300 . PMID 23646069 .
^ Седлак, Мариан (1 марта 2006 г.). «Крупномасштабная супрамолекулярная структура в растворах соединений с низкой молярной массой и смесей жидкостей: I. Характеристика рассеяния света» . Журнал физической химии б . 110 (9): 4329–4338. doi : 10.1021/jp0569335 . ISSN 1520-6106 . PMID 16509731 .
^ Díaz -Lasprilla, Ana M.; Меркадо, Рональд А.; Рамирес -Кабалеро, Густаво Э. (20 июня 2021 г.). «Эффект степени полимеризации глицерина на эмульгирующие свойства сложных эфиров полиглицерина» . Журнал прикладной полимерной науки . 138 (24): 50566. DOI : 10.1002/APP.50566 . ISSN 0021-8995 . S2CID 233888953 .
^ «Димеризация бычьего сывороточного альбумина, о чем свидетельствует размер частиц и измерение молекулярной массы :: anton-paar.com» . Антон Паар . Получено 14 июня 2022 года .

Внешние ссылки

[1] А. Эйнштейн (1910). «Теория опалесценции гомогенных жидкостей и жидких смесей вблизи критического состояния» . Анналы физики . 33 (16): 1275. Bibcode : 1910anp ... 338.1275e . Doi : 10.1002/andp.19103381612 .

[2] CV Raman (1927). «Соотношение эффекта Тиндалла с осмотическим давлением в коллоидных растворах». Индиан Дж. Физ . 2 : 1.

[3] P.Debye (1944). «Световой рассеяние в решениях». J. Appl. Физический 15 (4): 338. Bibcode : 1944jap .... 15..338d . doi : 10.1063/1.1707436 .

[4] BH ZIMM (1945). «Молекулярная теория рассеяния света в жидкостях». J. Chem. Физический 13 (4): 141. Bibcode : 1945jchph..13..141z . doi : 10.1063/1.1724013 .

[Zimm1948-5] Подпрыгнуть до: ^а ^{беременный} BH ZIMM (1948). «Разброс света и радиальное распределение функции высокополимерных растворов». J. Chem. Физический 16 (12): 1093. Bibcode : 1948jchph..16.1093Z . doi : 10.1063/1.1746738 .

[6] Iemenz, Paul C.; Лодж, Тимоти П. (2007). Полимер (2 -е изд.). Рот Ратона, Фл. [UU]: CRC Press. стр. 307–308. ISBN 978-1-57444-779-8 .

[7] «Измерение молекулярной массы с использованием статического рассеяния света :: Anton Paar Wiki» . Антон Паар . Получено 23 сентября 2022 года .

[8] Чанг, Цин (2016), «Осмотическое давление» , коллоидная и графическая химия для контроля качества воды , Elsevier, стр. 37–47, doi : 10.1016/b978-0-12-809315-3.00004-9 , ISBN 978-0-12-809315-3 , Получено 14 июня 2022 года

[9] Schaetzel, K. (1991). «Подавление многократного рассеяния с помощью методов кросс-корреляции фотонов». J. MOD Опт . 38 : SA393 - SA398. Bibcode : 1990jpcm .... 2..393s . doi : 10.1088/0953-8984/2/с/062 . S2CID 250745836 .

[10] Urban, C.; Schurtenberger, P. (1998). «Характеристика мутных коллоидных суспензий с использованием методов рассеяния света в сочетании с методами кросс-корреляции». J. Colloid Interface Sci . 207 (1): 150–158. Bibcode : 1998JCIS..207..150U . doi : 10.1006/jcis.1998.5769 . PMID 9778402 .

[11] Блок, я.; Scheffold, F. (2010). «Модулированное трехмерное рассеяние света поперечного корреляции: улучшение мутной характеристики образца». Обзор научных инструментов . 81 (12): 123107–123107–7. Arxiv : 1008.0615 . BIBCODE : 2010RSCI ... 81L3107B . doi : 10.1063/1.3518961 . PMID 21198014 . S2CID 9240166 .

[12] Пьюзи Пн (1999). «Подавление множественного рассеяния с помощью методов кросс-корреляции фотонов». Текущее мнение в области коллоидов и интерфейса . 4 (3): 177–185. doi : 10.1016/s1359-0294 (99) 00036-9 .

[13] Некоторые, Д. (2013). «Световой рассеянный анализ биомолекулярных взаимодействий» . Биофиз. Преподобный 5 (2): 147–158. doi : 10.1007/s12551-013-0107-1 . PMC 3641300 . PMID 23646069 .

[14] Седлак, Мариан (1 марта 2006 г.). «Крупномасштабная супрамолекулярная структура в растворах соединений с низкой молярной массой и смесей жидкостей: I. Характеристика рассеяния света» . Журнал физической химии б . 110 (9): 4329–4338. doi : 10.1021/jp0569335 . ISSN 1520-6106 . PMID 16509731 .

[15] Díaz -Lasprilla, Ana M.; Меркадо, Рональд А.; Рамирес -Кабалеро, Густаво Э. (20 июня 2021 г.). «Эффект степени полимеризации глицерина на эмульгирующие свойства сложных эфиров полиглицерина» . Журнал прикладной полимерной науки . 138 (24): 50566. DOI : 10.1002/APP.50566 . ISSN 0021-8995 . S2CID 233888953 .

[16] «Димеризация бычьего сывороточного альбумина, о чем свидетельствует размер частиц и измерение молекулярной массы :: anton-paar.com» . Антон Паар . Получено 14 июня 2022 года .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]