Рассеяние Ми

Рассеяние Ми при изменении диаметра частицы от 0,1 длины волны до 1 длины волны. Показатель преломления сферы равен 1,5.

Рассеяние Ми, художественный взгляд (Падающая плоская волна с линейной поляризацией, рассеянная октуполярным резонансом)

Резонансы Ми в зависимости от радиуса

Моностатическое радиолокационное сечение (ЭПР) идеально проводящей металлической сферы как функция частоты (рассчитано по теории Ми). В пределе низкочастотного рэлеевского рассеяния , когда длина окружности меньше длины волны, нормированная ЭПР равна ${\tfrac {\sigma }{\pi R^{2}}}\sim 9(kR)^{4}.$ В высокочастотном оптическом пределе ${\tfrac {\sigma }{\pi R^{2}}}\sim 1.$

В электромагнетизме решение Ми уравнений Максвелла (также известное как решение Лоренца-Ми , решение Лоренца-Ми-Дебая или рассеяние Ми ) описывает рассеяние электромагнитной плоской волны на однородной сфере . Решение принимает форму бесконечной серии сферических мультипольных парциальных волн . Он назван в честь немецкого физика Густава Ми .

Термин «решение Ми» также используется для обозначения решений уравнений Максвелла для рассеяния на стратифицированных сферах или бесконечных цилиндрах, а также для других геометрий, где можно написать отдельные уравнения для радиальной и угловой зависимости решений. Термин «теория Ми» иногда используется для обозначения этого набора решений и методов; это не относится к независимой физической теории или закону. В более широком смысле, формулы «рассеяния Ми» наиболее полезны в ситуациях, когда размер рассеивающих частиц сравним с длиной волны света, а не намного меньше или намного больше.

Рассеяние Ми (иногда называемое немолекулярным рассеянием или рассеянием аэрозольных частиц ) происходит в нижних слоях атмосферы на высоте 4500 м (15 000 футов) , множество по существу сферических частиц с диаметром, примерно равным длине волны падающего луча. где может находиться подарок. Теория рассеяния Ми не имеет ограничений по верхнему размеру и сходится к пределу геометрической оптики для больших частиц.

Введение

Угловая часть магнитных и электрических векторных сферических гармоник. Красные и зеленые стрелки показывают направление поля. Также представлены производящие скалярные функции, показаны только первые три порядка (диполи, квадруполи, октуполи).

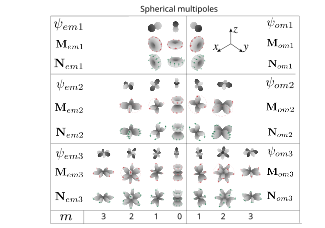
Современную формулировку решения Ми задачи рассеяния на сфере можно найти во многих книгах, например, в Дж. А. Стрэттона «Электромагнитной теории» . В этой формулировке падающая плоская волна, как и поле рассеяния, разлагается на излучающие сферические векторные сферические гармоники . Внутреннее поле разлагается до регулярных векторных сферических гармоник. Установив граничное условие на сферической поверхности, можно вычислить коэффициенты разложения рассеянного поля.

Для частиц, размер которых намного больше или меньше длины волны рассеянного света, существуют простые и точные приближения, достаточные для описания поведения системы. Но для объектов, размер которых находится в пределах нескольких порядков длины волны, например, капель воды в атмосфере, частиц латекса в краске, капель в эмульсиях, включая молоко, биологических клетках и клеточных компонентах, необходим более детальный подход.

Решение Ми назван в честь своего разработчика, немецкого физика Густава Ми . Датский физик Людвиг Лоренц и другие независимо разработали теорию рассеяния плоских электромагнитных волн диэлектрической сферой.

Этот формализм позволяет рассчитывать электрические и магнитные поля внутри и снаружи сферического объекта и обычно используется для расчета либо того, сколько света рассеивается (полное оптическое сечение ), либо куда он направляется (фактор формы). Примечательной особенностью этих результатов являются резонансы Ми, размеры которых разбросаны особенно сильно или слабо. Это контрастирует с рассеянием Рэлея для мелких частиц и рассеянием Рэлея-Ганса-Дебая (после лорда Рэлея , Ричарда Ганса и Питера Дебая ) для крупных частиц. Существование резонансов и других особенностей рассеяния Ми делает его особенно полезным формализмом при использовании рассеянного света для измерения размера частиц.

Приближения

Рэлеевское приближение (рассеяние)

Основная статья: Рэлеевское рассеяние

Изменение цвета неба на закате (красный ближе к солнцу, синий дальше всего) вызвано рэлеевским рассеянием на частицах атмосферного газа, длина которых намного меньше длины волны видимого света. Серо-белый цвет облаков вызван рассеянием Ми каплями воды, размер которых сопоставим с длинами волн видимого света.

Рэлеевское рассеяние описывает упругое рассеяние света сферами, размер которых намного меньше длины волны света. Интенсивность I рассеянного излучения определяется выражением

$I=I_{0}\left({\frac {1+\cos ^{2}\theta }{2R^{2}}}\right)\left({\frac {2\pi }{\lambda }}\right)^{4}\left({\frac {n^{2}-1}{n^{2}+2}}\right)^{2}\left({\frac {d}{2}}\right)^{6},$

где I ₀ — интенсивность света до взаимодействия с частицей, R — расстояние между частицей и наблюдателем, θ — угол рассеяния, λ — длина волны рассматриваемого света, n — показатель преломления частицы, и d – диаметр частицы.

Из приведенного выше уравнения видно, что рэлеевское рассеяние сильно зависит от размера частицы и длины волны. Интенсивность рэлеевского рассеянного излучения быстро возрастает с увеличением отношения размера частиц к длине волны. При этом интенсивность рэлеевского рассеянного излучения одинакова в прямом и обратном направлениях.

Модель рэлеевского рассеяния не работает, когда размер частиц становится больше примерно 10% длины волны падающего излучения. В случае частиц с размерами больше этого можно использовать модель рассеяния Ми для определения интенсивности рассеянного излучения. Интенсивность рассеянного Ми излучения определяется суммированием бесконечного ряда слагаемых, а не простым математическим выражением. Однако можно показать, что рассеяние в этом диапазоне размеров частиц отличается от рэлеевского рассеяния в нескольких отношениях: оно примерно не зависит от длины волны и больше в прямом направлении, чем в обратном. Чем больше размер частиц, тем больше света рассеивается в прямом направлении.

Голубой цвет неба является результатом рэлеевского рассеяния, поскольку размер частиц газа в атмосфере намного меньше длины волны видимого света. Рэлеевское рассеяние для синего света намного больше, чем для других цветов, из-за его более короткой длины волны. Когда солнечный свет проходит через атмосферу, его синий компонент является рэлеевским, сильно рассеиваемым атмосферными газами, а более длинноволновые компоненты (например, красный/желтый) — нет. Поэтому солнечный свет, приходящий прямо от Солнца, кажется слегка желтым, а свет, рассеянный по остальной части неба, кажется голубым. Во время восхода и заката влияние рэлеевского рассеяния на спектр проходящего света намного сильнее из-за большего расстояния, которое лучи света должны пройти через воздух с высокой плотностью у поверхности Земли.

Напротив, капли воды, из которых состоят облака, имеют размер, сравнимый с длинами волн видимого света, а рассеяние описывается моделью Ми, а не моделью Рэлея. Здесь все длины волн видимого света рассеиваются примерно одинаково, поэтому облака кажутся белыми или серыми.

Приближение Рэлея – Ганса

Приближение Рэлея -Ганса является приближенным решением проблемы рассеяния света, когда относительный показатель преломления частицы близок к показателю преломления окружающей среды, а ее размер намного меньше по сравнению с длиной волны света, деленной на | n − 1|, где n — показатель преломления :

${\begin{aligned}|n-1|&\ll 1\\kd|n-1|&\ll 1\end{aligned}}$

где ${\textstyle k}$ волновой вектор света ( ${\textstyle k={\frac {2\pi }{\lambda }}}$), и $d$ относится к линейному размеру частицы. Первое условие часто называют оптически мягким , и приближение справедливо для частиц произвольной формы.

Аномальное дифракционное приближение Ван де Хюлста

Приближение аномальной дифракции справедливо для больших (по сравнению с длиной волны) и оптически мягких сфер; мягкий в контексте оптики подразумевает, что показатель преломления частицы (m) лишь незначительно отличается от показателя преломления окружающей среды, и частица подвергает волну лишь небольшому фазовому сдвигу. Эффективность гашения в этом приближении определяется выражением

$Q=2-{\frac {4}{p}}\sin p+{\frac {4}{p^{2}}}(1-\cos p),$

где Q — коэффициент эффективности рассеяния, который определяется как отношение сечения рассеяния и геометрического сечения π a ² .

Член p = 4πa( n − 1)/λ имеет физический смысл фазовой задержки волны, проходящей через центр сферы, где a — радиус сферы, n — отношение показателей преломления внутри и снаружи сферы. сфера, а λ — длина волны света.

Эта система уравнений была впервые описана ван де Хюльстом в (1957).

Математика

Рассеяние плоской волны, направление падения параллельно оси z , поляризация параллельна оси x , радиус наночастицы a

Рассеяние сферической наночастицей решается точно независимо от размера частицы. Рассмотрим рассеяние на плоской волне, распространяющейся вдоль оси z , поляризованной вдоль оси x . Диэлектрическая и магнитная проницаемости частицы равны $\varepsilon _{1}$ и $\mu _{1}$, и $\varepsilon$ и $\mu$ для окружающей среды.

Чтобы решить проблему рассеяния, запишем сначала решения векторного уравнения Гельмгольца в сферических координатах, так как ему должны удовлетворять поля внутри и снаружи частиц. Уравнение Гельмгольца:

$\nabla ^{2}\mathbf {E} +{k}^{2}\mathbf {E} =0,\quad \nabla ^{2}\mathbf {H} +{k}^{2}\mathbf {H} =0.$

Помимо уравнения Гельмгольца поля должны удовлетворять условиям $\nabla \cdot \mathbf {E} =\nabla \cdot \mathbf {H} =0$ и $\nabla \times \mathbf {E} =i\omega \mu \mathbf {H}$, $\nabla \times \mathbf {H} =-i\omega \varepsilon \mathbf {E}$. Векторные сферические гармоники обладают всеми необходимыми свойствами, которые заключаются в следующем:

$\mathbf {M} _{^{e}_{o}mn}=\nabla \times \left(\mathbf {r} \psi _{^{e}_{o}mn}\right)$ — магнитные гармоники (ТЕ),

$\mathbf {N} _{^{e}_{o}mn}={\frac {\nabla \times \mathbf {M} _{^{e}_{o}mn}}{k}}$ — электрические гармоники (ТМ),

где

${\psi _{emn}=\cos m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r),}$

${\psi _{omn}=\sin m\varphi P_{n}^{m}(\cos \vartheta )z_{n}({k}r),}$

и $P_{n}^{m}(\cos \theta )$ — Ассоциированные полиномы Лежандра и $z_{n}({k}r)$ — любая из сферических функций Бесселя .

Далее разложим падающую плоскую волну по векторным сферическим гармоникам:

${\begin{aligned}\mathbf {E} _{\text{inc}}&=E_{0}e^{ikr\cos \theta }\mathbf {e} _{x}=E_{0}\sum _{n=1}^{\infty }i^{n}{\frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{o1n}^{(1)}(k,\mathbf {r} )-i\mathbf {N} _{e1n}^{(1)}(k,\mathbf {r} )\right),\\\mathbf {H} _{\text{inc}}&={\frac {-k}{\omega \mu }}E_{0}\sum _{n=1}^{\infty }i^{n}{\frac {2n+1}{n(n+1)}}\left(\mathbf {M} _{e1n}^{(1)}(k,\mathbf {r} )+i\mathbf {N} _{o1n}^{(1)}(k,\mathbf {r} )\right).\end{aligned}}$

Здесь верхний индекс $(1)$ означает, что в радиальной части функций $\psi _{^{e}_{o}mn}$ являются сферическими функциями Бесселя первого рода.Коэффициенты разложения получаются взятием интегралов вида

${\frac {\int _{0}^{2\pi }\int _{0}^{\pi }\mathbf {E} _{\text{inc}}\cdot \mathbf {M} _{^{e}_{o}mn}^{(1)}\sin \theta d\theta d\varphi }{\int _{0}^{2\pi }\int _{0}^{\pi }\left|\mathbf {M} _{^{e}_{o}mn}^{(1)}\right|^{2}\sin \theta d\theta d\varphi }}.$

В этом случае все коэффициенты при $m\neq 1$ равны нулю, так как интеграл по углу $\varphi$ в числителе равен нулю.

Тогда накладываются следующие условия:

1. Условия взаимодействия на границе сферы и среды (позволяющие связать коэффициенты разложения падающего, внутреннего и рассеянного полей)
2. Условие ограниченности решения в начале координат (следовательно, в радиальной части производящих функций $\psi _{^{e}_{o}mn}$для внутреннего поля выбраны сферические функции Бесселя первого рода),
3. Для рассеянного поля асимптотика на бесконечности соответствует расходящейся сферической волне (в связи с этим для рассеянного поля в радиальной части производящих функций $\psi _{^{e}_{o}mn}$ выбраны сферические функции Ганкеля первого рода).

Рассеянные поля записываются в терминах векторного гармонического разложения как

$\mathbf {E} _{s}=\sum _{n=1}^{\infty }E_{n}\left(ia_{n}\mathbf {N} _{e1n}^{(3)}(k,\mathbf {r} )-b_{n}\mathbf {M} _{o1n}^{(3)}(k,\mathbf {r} )\right),$

$\mathbf {H} _{s}={\frac {k}{\omega \mu }}\sum _{n=1}^{\infty }E_{n}\left(a_{n}\mathbf {M} _{e1n}^{(3)}(k,\mathbf {r} )+ib_{n}\mathbf {N} _{o1n}^{(3)}(k,\mathbf {r} )\right).$

Здесь верхний индекс $(3)$ означает, что в радиальной части функций $\psi _{^{e}_{o}mn}$ являются сферическими функциями Ганкеля первого рода (вторые функции имели бы $(4)$), и $E_{n}={\frac {i^{n}E_{0}(2n+1)}{n(n+1)}}$,

Внутренние поля:

$\mathbf {E} _{1}=\sum _{n=1}^{\infty }E_{n}\left(-id_{n}\mathbf {N} _{e1n}^{(1)}(k_{1},\mathbf {r} )+c_{n}\mathbf {M} _{o1n}^{(1)}(k_{1},\mathbf {r} )\right),$

$\mathbf {H} _{1}={\frac {-k_{1}}{\omega \mu _{1}}}\sum _{n=1}^{\infty }E_{n}\left(d_{n}\mathbf {M} _{e1n}^{(1)}(k_{1},\mathbf {r} )+ic_{n}\mathbf {N} _{o1n}^{(1)}(k_{1},\mathbf {r} )\right).$

${\textstyle k={\frac {\omega }{c}}n}$ волновой вектор вне частицы ${\textstyle k_{1}={\frac {\omega }{c}}{n_{1}}}$ – волновой вектор в среде из материала частицы, $n$ и $n_{1}$ – показатели преломления среды и частицы.

После применения условий интерфейса получаем выражения для коэффициентов:

$c_{n}(\omega )={\frac {\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-\mu _{1}\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},$

$d_{n}(\omega )={\frac {\mu _{1}n_{1}n\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-\mu _{1}n_{1}n\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\mu n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},$

$b_{n}(\omega )={\frac {\mu _{1}\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )}{\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},$

$a_{n}(\omega )={\frac {\mu n_{1}^{2}\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )}{\mu n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu _{1}n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},$

где

$\rho =ka,$

$\rho _{1}=k_{1}a$ с $a$ является радиусом сферы.

$j_{n}$ и $h_{n}$ представляют собой сферические функции Бесселя и Ганкеля первого рода соответственно.

Сечения рассеяния и затухания

Спектр мультипольного разложения сечения рассеяния золотой наносферой радиусом 100 нм

Спектр мультипольного разложения сечения рассеяния наносферой радиусом 100 нм и показателем преломления n=4

Спектр мультипольного разложения сечения рассеяния кремниевой наносферой радиусом 100 нм

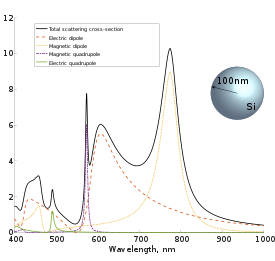
Значения, обычно рассчитываемые с использованием теории Ми, включают коэффициенты эффективности вымирания. $Q_{e}$, рассеяние $Q_{s}$и поглощение $Q_{a}$. Эти коэффициенты эффективности представляют собой отношения сечения соответствующего процесса, $\sigma _{i}$, в зону защиты от частиц, $Q_{i}={\frac {\sigma _{i}}{\pi a^{2}}}$, где a — радиус частицы. Согласно определению вымирания,

$\sigma _{e}=\sigma _{s}+\sigma _{a}$ и $Q_{e}=Q_{s}+Q_{a}$.

Коэффициенты рассеяния и затухания можно представить в виде бесконечного ряда:

$Q_{s}={\frac {2}{k^{2}a^{2}}}\sum _{n=1}^{\infty }(2n+1)\left(|a_{n}|^{2}+|b_{n}|^{2}\right)$

$Q_{e}={\frac {2}{k^{2}a^{2}}}\sum _{n=1}^{\infty }(2n+1)\Re (a_{n}+b_{n})$

Вклады в эти суммы, индексированные n , соответствуют порядкам мультипольного разложения , где n = 1 является дипольным членом, n = 2 является квадрапольным членом и т. д.

Применение к более крупным частицам

Если размер частицы равен нескольким длинам волн в материале, то рассеянные поля имеют некоторые особенности.Далее мы поговорим о форме электрического поля, так как магнитное поле получается из него взятием ротора .

Все коэффициенты Ми зависят от частоты и имеют максимумы, когда знаменатель близок к нулю (точное равенство нулю достигается для комплексных частот). В этом случае возможно, что в рассеянии доминирует вклад одной конкретной гармоники. Тогда на больших расстояниях от частицы диаграмма направленности рассеянного поля будет аналогична соответствующей диаграмме направленности угловой части векторных сферических гармоник. Гармоники $\mathbf {N} _{^{e}_{o}m1}$ соответствуют электрическим диполям (если вклад этой гармоники доминирует в расширении электрического поля, то поле аналогично полю электрического диполя), $\mathbf {M} _{^{e}_{o}m1}$ соответствуют электрическому полю магнитного диполя, $\mathbf {N} _{^{e}_{o}m2}$ и $\mathbf {M} _{^{e}_{o}m2}$ - электрические и магнитные квадруполи, $\mathbf {N} _{^{e}_{o}m3}$ и $\mathbf {M} _{^{e}_{o}m3}$ - октуполи и так далее. Максимумы коэффициентов рассеяния (а также изменение их фазы на $\pi$) называются мультипольными резонансами, а нули можно назвать анаполями .

Зависимость сечения рассеяния от длины волны и вклад специфических резонансов сильно зависят от материала частиц. Например, для частицы золота радиусом 100 нм вклад электрического диполя в рассеяние преобладает в оптическом диапазоне, а для частицы кремния наблюдаются ярко выраженные магнитно-дипольный и квадрупольный резонансы. Для металлических частиц пик, видимый в поперечном сечении рассеяния, также называется локализованным плазмонным резонансом .

В пределе малых частиц или длинных волн вклад электрического диполя доминирует в сечении рассеяния.

Другие направления падающей плоской волны

В случае плоской волны x- поляризации, падающей вдоль оси z , разложения всех полей содержали только гармоники с m = 1, но для произвольной падающей волны это не так. Для повернутой плоской волны коэффициенты разложения можно получить, например, используя тот факт, что при вращении векторные сферические гармоники преобразуются друг через друга с помощью D-матриц Вигнера .

В этом случае рассеянное поле будет разложено по всем возможным гармоникам:

$\mathbf {E} _{s}=\sum _{n=1}^{\infty }\sum _{m=0}^{n}E_{0}(D_{Memn}\mathbf {M} _{emn}^{(3)}(k,\mathbf {r} )+D_{Momn}\mathbf {M} _{omn}^{(3)}(k,\mathbf {r} )+D_{Nemn}\mathbf {N} _{emn}^{(3)}(k,\mathbf {r} )+D_{Nomn}\mathbf {N} _{omn}^{(3)}(k,\mathbf {r} ))$

Тогда сечение рассеяния будет выражаться через коэффициенты следующим образом:

$C_{\text{sca}}={\frac {2\pi }{\pi a^{2}k^{2}}}\sum _{n=1}^{\infty }{\frac {n(n+1)}{(2n+1)}}\times \left[\sum \limits _{m=1}^{n}{\frac {(n+m)!}{(n-m)!}}\left(|D_{Memn}|^{2}+|D_{Momn}|^{2}+|D_{Nemn}|^{2}+|D_{Nomn}|^{2}\right)+2|D_{Me0n}|^{2}+2|D_{Ne0n}|^{2}\right].$

Эффект подземелья

Эффект Керкера — это явление направленности рассеяния, которое возникает, когда присутствуют разные мультипольные отклики, которыми можно пренебречь.

Частный (диполярный) случай эффекта Керкера. Суммарное электрическое поле скрещенных магнитного и электрического диполей, излучающих синфазно. Диаграмма направленности несимметрична, в одну сторону поля взаимно разрушаются, а в другую складываются.

В 1983 году в работе Керкера Ванга и Джайлза , направление рассеяния частицами с $\mu \neq 1$ было расследовано. В частности, было показано, что для гипотетических частиц с $\mu =\varepsilon$ обратное рассеяние полностью подавляется. Это можно рассматривать как распространение на сферическую поверхность результатов Джайлза и Уайлда для отражения от плоской поверхности с одинаковыми показателями преломления, где отражение и пропускание постоянны и не зависят от угла падения.

Кроме того, сечения рассеяния в прямом и обратном направлениях просто выражаются через коэффициенты Ми:

${\begin{aligned}C_{\text{sca}}^{\text{backward}}&={\frac {1}{a^{2}k^{2}}}\left|\sum _{n=1}^{\infty }{(2n+1)}(-1)^{n}(a_{n}-b_{n})\right|^{2}\\C_{\text{sca}}^{\text{forward}}&={\frac {1}{a^{2}k^{2}}}\left|\sum _{n=1}^{\infty }{(2n+1)}(a_{n}+b_{n})\right|^{2}\end{aligned}}$

Для определенных комбинаций коэффициентов приведенные выше выражения можно минимизировать.

Так, например, когда условия с $n>1$ можно пренебречь ( дипольное приближение ), $(a_{1}-b_{1})=0$, соответствует минимуму обратного рассеяния (магнитные и электрические диполи равны по величине и находятся в фазе, это также называется первым условием Керкера или условием нулевой обратной интенсивности). ). И $(a_{1}+b_{1})=0$ соответствует минимуму рассеяния вперед, это также называется вторым условием Керкера (или условием почти нулевой прямой интенсивности ). Из оптической теоремы показано, что для пассивной частицы $(a_{1}=-b_{1})$ невозможно. Для точного решения задачи необходимо учесть вклады всех мультиполей. Сумма электрических и магнитных диполей образует источник Гюйгенса.

Для диэлектрических частиц максимальное рассеяние вперед наблюдается на длинах волн, превышающих длину волны магнитного дипольного резонанса, а максимальное рассеяние назад — на более коротких.

Позже были обнаружены и другие разновидности эффекта. Например, поперечный эффект Керкера с почти полным одновременнымподавление полей рассеяния как вперед, так и назад (картины бокового рассеяния), оптомеханический эффект Керкера, в акустическом рассеянии, а также встречается в растениях.

также есть короткое видео На YouTube с объяснением эффекта.

Диадическая функция Грина сферы

Функция Грина является решением следующего уравнения:

$\nabla \times \nabla \times {\bf {\hat {G}}}(\omega ,\mathbf {r} ,\mathbf {r} ')=\left({\frac {\omega }{c}}\right)^{2}\varepsilon (\mathbf {r} ,\omega ){\bf {\hat {G}}}(\omega ,\mathbf {r} ,\mathbf {r} ')+{\bf {\hat {1}}}\delta (\mathbf {r} -\mathbf {r} '),$

где ${\hat {\bf {1}}}$ — идентификационная матрица $\varepsilon (\mathbf {r} ,\omega )=\varepsilon _{1}(\omega )$ для $r<a$, и $\varepsilon (\mathbf {r} ,\omega )=\varepsilon$ для $r>a$. Поскольку все поля векторные, функция Грина представляет собой матрицу размером 3 на 3 и называется диадической. Если поляризация $\mathbf {P} (\mathbf {r} )$ индуцируется в системе, когда поля записаны в виде

$\mathbf {E} ^{\omega }({\mathbf {r} })=\omega ^{2}\mu \int \limits _{V}dV'{\hat {\bf {G}}}({\bf {r,r'}},k)\mathbf {P} ^{\omega }(\mathbf {r} ')$

Так же, как и поля, функцию Грина можно разложить на векторные сферические гармоники. Диадическая функция Грина свободного пространства а:

${\begin{aligned}&{\hat {\bf {G}}}^{0}({\mathbf {r} ,\mathbf {r} ',k})\\{}={}&{\frac {\mathbf {e_{r}} \otimes \mathbf {e_{r}} }{k^{2}}}\delta (\mathbf {r} -\mathbf {r} ')+{\frac {ik}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{(n+m)!}}\cdot {}\\&\quad {\begin{cases}\left(\left(\mathbf {M} _{emn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{emn}^{(3)}[k,\mathbf {r} ']+\mathbf {M} _{omn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{omn}^{(3)}[k,\mathbf {r} ']\right)+\left({\mathbf {N} }_{emn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{emn}^{(3)}[k,\mathbf {r} ']+\mathbf {N} _{omn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{omn}^{(3)}[k,\mathbf {r} ']\right)\right),&{\text{if }}r<r'\\\left(\left(\mathbf {M} _{emn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{emn}^{(1)}[k,\mathbf {r} ']+\mathbf {M} _{omn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{omn}^{(1)}[k,\mathbf {r} ']\right)+\left({\mathbf {N} }_{emn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{emn}^{(1)}[k,\mathbf {r} ']+\mathbf {N} _{omn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{omn}^{(1)}[k,\mathbf {r} ']\right)\right),&{\text{if }}r>r'\end{cases}}\end{aligned}}$

При наличии сферы функция Грина также разлагается на векторные сферические гармоники. Его внешний вид зависит от среды, в которой находятся точки. $\mathbf {r}$ и $\mathbf {r} '$ расположены.

Когда обе точки находятся вне сферы ( $r>a,r'>a$):

${\begin{aligned}&{\hat {\bf {G}}}^{00}({\mathbf {r} ,\mathbf {r} ',k,k_{1}})\\{}={}&{\hat {\bf {G}}}^{0}({\mathbf {r} ,\mathbf {r} ',k})+{\frac {ik}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{(n+m)!}}\cdot {}\\&\quad \left(a_{n}^{(0)}(\omega )\left(\mathbf {M} _{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ']\right)+b_{n}^{(0)}(\omega )\left({\mathbf {N} }_{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ']\right)\right)\end{aligned}}$

где коэффициенты:

${\begin{aligned}a_{n}^{(0)}(\omega )&={\frac {\mu /\mu _{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )-\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})}{\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu /\mu _{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},\\b_{n}^{(0)}(\omega )&={\frac {n^{2}\mu _{1}/\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )-n_{1}^{2}\left[\rho j_{n}(\rho )\right]'j_{n}(\rho _{1})}{n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-n^{2}\mu _{1}/\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}}.\end{aligned}}$

Когда обе точки находятся внутри сферы ( $r<a,r'<a$) :

${\begin{aligned}&{\hat {\bf {G}}}^{11}({\mathbf {r} ,\mathbf {r} ',k,k_{1}})\\{}={}&{\hat {\bf {G}}}^{0}({\mathbf {r} ,\mathbf {r} ',k_{1}})+{\frac {ik_{1}}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{(n+m)!}}\cdot {}\\&\quad \left(c_{n}^{(1)}(\omega )\left(\mathbf {M} _{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ]\otimes {\mathbf {M} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ']\right)+d_{n}^{(1)}(\omega )\left({\mathbf {N} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ]\otimes {\mathbf {N} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ']\right)\right),\end{aligned}}$

Коэффициенты:

${\begin{aligned}c_{n}^{(1)}(\omega )&={\frac {\mu _{1}/\mu \left[\rho h_{n}(\rho )\right]'h_{n}(\rho _{1})-\left[\rho _{1}h_{n}(\rho _{1})\right]'h_{n}(\rho )}{\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )-\mu _{1}/\mu \left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})}},\\d_{n}^{(1)}(\omega )&={\frac {n_{1}^{2}\mu /\mu _{1}\left[\rho h_{n}(\rho )\right]'h_{n}(\rho _{1})-n^{2}\left[\rho _{1}h_{n}(\rho _{1})\right]'h_{n}(\rho )}{n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )-n_{1}^{2}\mu /\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})}}.\end{aligned}}$

Источник находится внутри сферы, а точка наблюдения снаружи ( $r>a,r'<a$):

${\begin{aligned}&{\hat {\bf {G}}}^{01}({\mathbf {r} ,\mathbf {r} ',k,k_{1}})\\{}={}&{\frac {ik_{1}}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{(n+m)!}}\cdot {}\\&\quad \left(a_{n}^{(1)}(\omega )(\mathbf {M} _{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} '])+b_{n}^{(1)}(\omega )\left(\mathbf {N} _{^{e}_{o}mn}^{(3)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{^{e}_{o}mn}^{(1)}[k_{1},\mathbf {r} ']\right)\right)\end{aligned}}$

коэффициенты:

${\begin{aligned}a_{n}^{(1)}(\omega )&={\frac {\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho _{1})-\left[\rho _{1}h_{n}(\rho _{1})\right]'j_{n}(\rho _{1})}{\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )-\mu _{1}/\mu \left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})}},\\b_{n}^{(1)}(\omega )&={\frac {nn_{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho _{1})-nn_{1}\left[\rho _{1}h_{n}(\rho _{1})\right]'j_{n}(\rho _{1})}{n^{2}\mu _{1}/\mu \left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )-n_{1}^{2}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})}}.\end{aligned}}$

Источник находится вне сферы, а точка наблюдения внутри ( $r<a,r'>a$) :

${\begin{aligned}&{\hat {\bf {G}}}^{10}({\mathbf {r} ,\mathbf {r} ',k,k_{1}})\\{}={}&{\frac {ik}{4\pi }}\sum _{n=1}^{\infty }\sum _{m=0}^{n}(2-\delta _{m,0}){\frac {2n+1}{n(n+1)}}{\frac {(n-m)!}{(n+m)!}}\cdot {}\\&\quad \left(c_{n}^{(0)}(\omega )(\mathbf {M} _{^{e}_{o}mn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {M} }_{^{e}_{o}mn}^{(3)}[k_{1},\mathbf {r} '])+d_{n}^{(0)}(\omega )({\mathbf {N} }_{^{e}_{o}mn}^{(1)}[k,\mathbf {r} ]\otimes {\mathbf {N} }_{^{e}_{o}mn}^{(3)}[k_{1},\mathbf {r} '])\right)\end{aligned}}$

коэффициенты:

${\begin{aligned}c_{n}^{(0)}(\omega )&={\frac {\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-\mu /\mu _{1}\left[\rho _{1}j_{n}(\rho _{1})\right]'h_{n}(\rho )}},\\d_{n}^{(0)}(\omega )&={\frac {nn_{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho )-nn_{1}\left[\rho j_{n}(\rho )\right]'h_{n}(\rho )}{n_{1}^{2}\mu /\mu _{1}\left[\rho h_{n}(\rho )\right]'j_{n}(\rho _{1})-n^{2}\left[\rho _{1}j_{n}(\rho _{1})\right]'j_{n}(\rho )}}.\end{aligned}}$

Вычислительные коды

Решения Mie реализованы в ряде программ, написанных на разных компьютерных языках, таких как Fortran , MATLAB и Mathematica . Эти решения аппроксимируют бесконечный ряд и предоставляют на выходе расчет фазовой функции рассеяния, эффективности затухания, рассеяния и поглощения, а также других параметров, таких как параметры асимметрии или крутящий момент излучения. Текущее использование термина «решение Ми» указывает на рядную аппроксимацию решения уравнений Максвелла. Известно несколько объектов, допускающих такое решение: сферы, концентрические сферы, бесконечные цилиндры, группы сфер и группы цилиндров. Известны также рядовые решения для рассеяния на эллипсоидальных частицах. Список кодов, реализующих эти специализированные решения, представлен ниже:

• Коды электромагнитного рассеяния сферами – решения для одиночной сферы, сфер с покрытием, многослойной сферы и кластера сфер;
• Коды электромагнитного рассеяния цилиндрами – решения для одиночного цилиндра, многослойных цилиндров и группы цилиндров.

Обобщением, позволяющим рассматривать частицы более общей формы, является метод Т-матрицы , который также основан на рядной аппроксимации решений уравнений Максвелла.

См. также внешние ссылки на другие коды и калькуляторы.

Приложения

Теория Ми очень важна в метеорологической оптике , где отношения диаметра к длине волны порядка единицы и выше характерны для многих задач, касающихся дымки и рассеяния облаков . Еще одним применением является характеристика частиц с помощью измерений оптического рассеяния. Решение Ми также важно для понимания внешнего вида обычных материалов, таких как молоко , биологические ткани и латексная краска.

Атмосферная наука

Рассеяние Ми происходит, когда диаметры атмосферных частиц равны длинам волн света или превышают их. Пыль , пыльца , дым и микроскопические капли воды , образующие облака, являются частыми причинами рассеяния Ми. Рассеяние Ми происходит в основном в нижних частях атмосферы, где более крупные частицы более распространены, и преобладает в облачных условиях.

Обнаружение и скрининг рака

Теория Ми использовалась для определения того, соответствует ли рассеянный свет ткани ядрам здоровых или раковых клеток, с использованием низкокогерентной интерферометрии с угловым разрешением .

Клинический лабораторный анализ

Теория Ми является центральным принципом применения нефелометрических анализов, широко используемых в медицине для измерения различных белков плазмы . широкий спектр белков плазмы С помощью нефелометрии можно обнаружить и количественно оценить .

Магнитные частицы

Для магнитных сфер возникает ряд необычных эффектов электромагнитного рассеяния. Когда относительная диэлектрическая проницаемость равна проницаемости , коэффициент обратного рассеяния равен нулю. Кроме того, рассеянное излучение поляризовано в том же смысле, что и падающее. В пределе малых частиц (или длинноволновом) могут возникнуть условия нулевого рассеяния вперед, полной поляризации рассеянного излучения в других направлениях и асимметрии рассеяния вперед по отношению к обратному. Особый случай в пределе малых частиц обеспечивает интересные частные случаи полной поляризации и асимметрии рассеяния вперед-назад.

Метаматериал

Теория Ми использовалась для создания метаматериалов . Обычно они состоят из трехмерных композитов металлических или неметаллических включений, периодически или случайным образом внедренных в матрицу с низкой диэлектрической проницаемостью. В такой схеме отрицательные определяющие параметры создаются вокруг резонансов Ми включений: отрицательная эффективная диэлектрическая проницаемость создается вокруг резонанса коэффициента электрического дипольного рассеяния Ми, тогда как отрицательная эффективная проницаемость создается вокруг резонанса Ми коэффициент магнитно-дипольного рассеяния, а дважды отрицательный материал (ДНГ) создан на основе перекрытия резонансов электрического и магнитно-дипольного коэффициентов рассеяния Ми. Частица обычно имеет следующие комбинации:

1. один набор магнитодиэлектрических частиц со значениями относительной диэлектрической проницаемости и проницаемости, значительно превышающими единицу и близкими друг к другу;
2. две разные диэлектрические частицы с одинаковой диэлектрической проницаемостью, но разного размера;
3. две разные диэлектрические частицы одинакового размера, но с разной диэлектрической проницаемостью.

Теоретически частицы, анализируемые теорией Ми, обычно имеют сферическую форму, но на практике частицы обычно изготавливаются в виде кубов или цилиндров для простоты изготовления. Чтобы соответствовать критериям гомогенизации, которые можно сформулировать в виде того, что постоянная решетки намного меньше рабочей длины волны, относительная диэлектрическая проницаемость диэлектрических частиц должна быть намного больше 1, например $\varepsilon _{\text{r}}>78(38)$ для достижения отрицательной эффективной диэлектрической проницаемости (проницаемости).

Размер частиц

Теория Ми часто применяется в лазерном дифракционном анализе для проверки влияния размера частиц. В то время как первые компьютеры 1970-х годов могли рассчитывать данные дифракции только с помощью более простого приближения Фраунгофера, метод Ми широко используется с 1990-х годов и официально рекомендуется для частиц размером менее 50 микрометров в стандарте ISO 13320:2009.

Теория Ми использовалась для обнаружения концентрации нефти в загрязненной воде.

Рассеяние Ми - основной метод определения размера одиночных сонолюминесцентных пузырьков воздуха в воде. и справедливо для полостей в материалах, а также для частиц в материалах, пока окружающий материал по существу не поглощает влагу.

Паразитология

Его также использовали для изучения структуры Plasmodium falciparum , особо патогенной формы малярии .

Расширения

В 1986 году П. А. Бобберт и Дж. Влигер расширили модель Ми для расчета рассеяния на сфере в однородной среде, расположенной на плоской поверхности. Как и модель Ми, расширенную модель можно применять к сферам с радиусом, близким к длине волны падающего света. Существует код C++, реализующий модель Бобберта – Влигера (BV). Последние разработки связаны с рассеянием на эллипсоиде. Современные исследования опираются на известные исследования Рэлея.

См. также

• Коды электромагнитного рассеяния сферами
• Вычислительная электромагнетика
• Рассеяние света частицами
• Список кодов переноса атмосферного излучения
• Оптические свойства воды и льда

Дальнейшее чтение

• Керкер, М. (1969). Рассеяние света и других электромагнитных излучений . Нью-Йорк: Академик.
• Барбер, П.В.; Хилл, СС (1990). Рассеяние света частицами: Численные методы . Сингапур: World Scientific. ISBN  978-9971-5-0813-5 .
• Мищенко М.; Трэвис, Л.; Лацис, А. (2002). Рассеяние, поглощение и излучение света малыми частицами . Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-78252-4 .
• Фрисвад, Дж.; Кристенсен, Н.; Дженсен, Х. (2007). «Вычисление свойств рассеяния участвующих сред с использованием теории Лоренца-Ми» (PDF) . Транзакции ACM с графикой . 26 (3): 60. дои : 10.1145/1276377.1276452 .
• Вридт, Томас (2008). «Теория Мие 1908 года, на мобильном телефоне 2008 года». Журнал количественной спектроскопии и переноса излучения . 109 (8): 1543–1548. Бибкод : 2008JQSRT.109.1543W . дои : 10.1016/j.jqsrt.2008.01.009 .
• Лоренц, Людвиг (1890). «Движение света внутрь и наружу сферы, освещенной плоскими световыми волнами». Труды Датского королевского общества наук . 6 (6): 1–62.

Внешние ссылки

• SCATTERLIB и scattport.org — это коллекции кодов рассеяния света с реализациями решений Ми на FORTRAN , C++ , IDL , Pascal , Mathematica и Mathcad.
• JMIE (2D- код C++ для расчета аналитических полей вокруг бесконечного цилиндра, разработанный Джеффри М. МакМахоном)
• СкатЛаб . Программа рассеяния Ми для Windows.
• Код STRATIFY MatLab рассеяния на многослойных сферах в случаях, когда источником является точечный диполь и плоская волна. Описание в arXiv:2006.06512.
• Scattnlay с открытым исходным кодом, C++ — пакет решения Mie для содержащий оболочки Python и JavaScript . Предоставляет результаты моделирования в дальнем и ближнем поле для многослойных сфер.
• Онлайн-калькулятор рассеяния Ми обеспечивает моделирование свойств рассеяния (включая мультипольное разложение) и карты ближнего поля для объемных, ядро-оболочек и многослойных сфер. Параметры материала включают все файлы nk-data с сайта refractiveindex.info . Исходный код является частью проекта Scattnlay .
• онлайн-калькулятор решений Mie с документацией на немецком и английском языках. Доступен
• Онлайн-калькулятор рассеяния Ми создает красивые графики для различных параметров.
• phpMie Онлайн-калькулятор рассеяния Ми, написанный на PHP .
• Резонанс Ми обеспечивает диффузию света и случайную генерацию.
• Решение Ми для сферических частиц .
• PyMieScatt — пакет решений Mie, написанный на Python .
• pyMieForAll с открытым исходным кодом для C++ — пакет решения Mie и оболочкой Python .