Модель асимптотического усиления

Модель асимптотического усиления (также известный как метод Розенштарка) ) представляет собой представление усиления усилителей с отрицательной обратной связью, определяемое асимптотическим соотношением усиления:

$G=G_{\infty }\left({\frac {T}{T+1}}\right)+G_{0}\left({\frac {1}{T+1}}\right)\ ,$

где $T$ – коэффициент возврата при отключенном входном источнике (равен отрицательному коэффициенту усиления контура в случае одноконтурной системы, состоящей из односторонних блоков), G _∞ – асимптотический коэффициент усиления и G ₀ – член прямой передачи. Эта форма усиления может дать интуитивное представление о схеме, и ее зачастую легче получить, чем прямую атаку на усиление.

Рисунок 1: Блок-схема модели асимптотического усиления.

На рисунке 1 показана блок-схема, которая приводит к выражению асимптотического усиления. Асимптотическое соотношение усиления также можно выразить в виде графа потока сигналов . См. рисунок 2. Модель асимптотического усиления является частным случаем теоремы о дополнительных элементах .

Рисунок 2: Возможный эквивалентный график потока сигналов для модели асимптотического усиления

Как следует непосредственно из предельных случаев выражения выигрыша, асимптотический выигрыш G _∞ представляет собой просто выигрыш системы при стремлении коэффициента отдачи к бесконечности:

$G_{\infty }=G\ {\Big |}_{T\rightarrow \infty }\ ,$

тогда как член прямой передачи G ₀ представляет собой выигрыш системы, когда коэффициент возврата равен нулю:

$G_{0}=G\ {\Big |}_{T\rightarrow 0}\ .$

Преимущества

• Эта модель полезна, поскольку она полностью характеризует усилители с обратной связью, включая эффекты нагрузки и двусторонние свойства усилителей и цепей обратной связи.
• Часто усилители с обратной связью проектируются так, что коэффициент возврата T намного превышает единицу. В этом случае, предполагая, что член прямой передачи G ₀ мал (как это часто бывает), коэффициент усиления G системы примерно равен асимптотическому коэффициенту усиления G _∞ .
• Асимптотический коэффициент усиления (обычно) является функцией только пассивных элементов схемы и часто может быть найден путем проверки.
• Топологию обратной связи (последовательный-последовательный, последовательно-шунтирующий и т. д.) не требуется определять заранее, поскольку анализ во всех случаях один и тот же.

Выполнение

Непосредственное применение модели включает в себя следующие шаги:

1. Выберите зависимый источник в схеме.
2. Найдите коэффициент возврата для этого источника.
3. Найдите коэффициент усиления G _∞ непосредственно из схемы, заменив схему на схему, соответствующую T = ∞.
4. Коэффициент усиления G ₀ найти непосредственно из схемы, заменив схему на схему, соответствующую Т = 0.
5. Подставьте значения T, G _∞ и G ₀ в формулу асимптотического усиления.

Эти шаги можно реализовать непосредственно в SPICE, используя слабосигнальную схему анализа рук. При таком подходе обеспечивается легкий доступ к зависимым источникам устройств. Напротив, для экспериментальных измерений с использованием реальных устройств или моделирования SPICE с использованием численно созданных моделей устройств с недоступными зависимыми источниками оценка коэффициента возврата требует специальных методов .

Связь с классической теорией обратной связи

Классическая теория обратной связи пренебрегает прямой связью ( G ₀ ). Если упреждающая связь исключена, выигрыш от модели асимптотического усиления становится

$G=G_{\infty }{\frac {T}{1+T}}={\frac {G_{\infty }T}{1+{\frac {1}{G_{\infty }}}G_{\infty }T}}\ ,$

разомкнутого контура в то время как в классической теории обратной связи, с точки зрения усиления A , коэффициент усиления с обратной связью (коэффициент усиления замкнутого контура) равен:

$A_{\mathrm {FB} }={\frac {A}{1+{\beta }_{\mathrm {FB} }A}}\ .$

Сравнение двух выражений показывает, что коэффициент обратной связи β _FB равен:

$\beta _{\mathrm {FB} }={\frac {1}{G_{\infty }}}\ ,$

в то время как коэффициент усиления в разомкнутом контуре составляет:

$A=G_{\infty }\ T\ .$

Если точность достаточна (обычно так и есть), эти формулы предлагают альтернативную оценку T : оценить коэффициент усиления разомкнутого контура и G _∞ и использовать эти выражения для T. нахождения Часто эти две оценки проще, чем оценка Т. непосредственная

Примеры

Ниже описаны шаги по получению коэффициента усиления с использованием асимптотической формулы коэффициента усиления для двух усилителей с отрицательной обратной связью. Пример с одним транзистором показывает, как метод работает в принципе для усилителя крутизны, а второй пример с двумя транзисторами показывает подход к более сложным случаям с использованием усилителя тока.

Однокаскадный транзисторный усилитель

Рисунок 3. Усилитель с обратной связью на полевом транзисторе

Рассмотрим простой усилитель с обратной связью на полевом транзисторе , показанный на рисунке 3. Цель состоит в том, чтобы найти низкочастотный коэффициент усиления транссопротивления этой схемы при разомкнутой цепи G = v _out / i _с использованием асимптотической модели усиления.

Рисунок 4: Схема слабого сигнала для трансрезистивного усилителя; резистор обратной связи R _f расположен под усилителем, чтобы напоминать стандартную топологию.

Рисунок 5. Схема слабого сигнала с обрывом обратного пути и усилителем испытательного напряжения при обрыве.

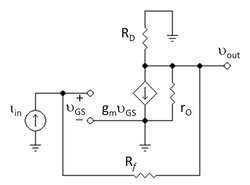
Эквивалентная схема слабого сигнала показана на рисунке 4, где транзистор заменен моделью гибридного пи .

Коэффициент возврата

Проще всего начать с определения коэффициента отдачи T , поскольку G ₀ и G _∞ определяются как предельные формы выигрыша, поскольку T стремится либо к нулю, либо к бесконечности. Чтобы взять эти пределы, необходимо знать, параметр T. от чего зависит В этой схеме есть только один зависимый источник, поэтому в качестве отправной точки определяется коэффициент возврата, связанный с этим источником, как описано в статье о коэффициенте возврата .

Коэффициент возврата можно найти с помощью рисунка 5. На рисунке 5 источник входного тока установлен на ноль. Отключив зависимый источник от выходной стороны цепи и закоротив его клеммы, выходная сторона схемы будет изолирован от входа и петля обратной связи разрывается. Испытательный ток заменяет _. зависимый источник Затем находится обратный ток, создаваемый в зависимом источнике испытательным током. Коэффициент возврата тогда равен T = - i _r / i _t . Используя этот метод и учитывая, что R _D параллельно r _O , T определяется как:

$T=g_{\mathrm {m} }\left(R_{\mathrm {D} }\ ||r_{\mathrm {O} }\right)\approx g_{\mathrm {m} }R_{\mathrm {D} }\ ,$

где приближение является точным в общем случае, когда r _O >> R _D . С учетом этого соотношения ясно, что пределы T → 0 или ∞ реализуются, если мы допускаем крутизну g _m → 0 или ∞.

Асимптотический выигрыш

Нахождение асимптотического усиления G _∞ дает понимание и обычно может быть выполнено путем проверки. Чтобы найти G _∞, положим g _m → ∞ и найдем результирующий выигрыш. Ток стока i _D = g _m v _GS должен быть конечным. Следовательно, когда g _m стремится к бесконечности, v _GS также должен стремиться к нулю. Поскольку источник заземлен, v _GS подразумевает v _{G = 0.} = 0 также При v _G = 0 и том факте, что весь входной ток протекает через R _f (поскольку полевой транзистор имеет бесконечное входное сопротивление), выходное напряжение просто – i _в R _f . Следовательно

$G_{\infty }={\frac {v_{\mathrm {out} }}{i_{\mathrm {in} }}}=-R_{\mathrm {f} }\ .$

В качестве альтернативы G _∞ — это коэффициент усиления, полученный путем замены транзистора идеальным усилителем с бесконечным коэффициентом усиления — нулевым значением .

Прямое проходное соединение

Чтобы найти прямое соединение $G_{0}$ мы просто допускаем g _m → 0 и вычисляем полученный выигрыш. Токи через R _f и параллельную комбинацию R _D || Следовательно, r _O должно быть таким же и равным i _в . Таким образом, выходное напряжение равно i _in ( _RD || r _O ) .

Следовательно

$G_{0}={\frac {v_{out}}{i_{in}}}=R_{D}\|r_{O}\approx R_{D}\ ,$

где приближение является точным в общем случае, когда r _O >> R _D .

Общий выигрыш

Таким образом, общий коэффициент усиления транссопротивления этого усилителя составит:

$G={\frac {v_{out}}{i_{in}}}=-R_{f}{\frac {g_{m}R_{D}}{1+g_{m}R_{D}}}+R_{D}{\frac {1}{1+g_{m}R_{D}}}={\frac {R_{D}\left(1-g_{m}R_{f}\right)}{1+g_{m}R_{D}}}\ .$

При рассмотрении этого уравнения оказывается, что выгодно сделать R _D большим, чтобы общий коэффициент усиления приближался к асимптотическому коэффициенту усиления, что делает коэффициент усиления нечувствительным к параметрам усилителя ( g _m и R _D ). Кроме того, большой первый член снижает важность коэффициента прямого прохождения, который ухудшает качество усилителя. Одним из способов увеличения R _Д является замена этого резистора активной нагрузкой , например токовым зеркалом .

Рисунок 6: Двухтранзисторный усилитель с обратной связью; любой импеданс источника приравнивается _RS к базовому резистору R _B .

Двухкаскадный транзисторный усилитель

Рисунок 7: Схема использования модели асимптотического усиления; параметр α = β/(β+1); резистор R _C = R _C1 .

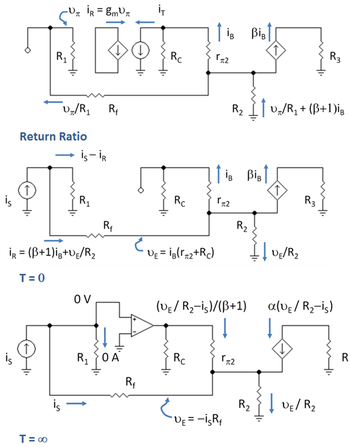
На рисунке 6 показан двухтранзисторный усилитель с резистором обратной связи R _ф . Этот усилитель часто называют усилителем с обратной связью с шунтовой последовательностью и анализируют на основе того, что резистор R ₂ включен последовательно с выходом и измеряет выходной ток, в то время как R _f включен (параллельно) с входом и вычитает из него входной ток. См. статью об усилителе с отрицательной обратной связью и ссылки Мейера или Седры. То есть усилитель использует обратную связь по току. Часто неясно, какой тип обратной связи используется в усилителе, и подход с асимптотическим усилением имеет то преимущество/недостаток, что он работает независимо от того, понимаете ли вы схему.

На рисунке 6 указан выходной узел, но не указан выбор выходной переменной. В дальнейшем в качестве выходной переменной выбирается ток короткого замыкания усилителя, то есть ток коллектора выходного транзистора. Другие варианты вывода обсуждаются позже.

Чтобы реализовать модель асимптотического усиления, можно использовать зависимый источник, связанный с любым транзистором. Здесь выбран первый транзистор.

Коэффициент возврата

Схема для определения коэффициента возврата показана на верхней панели рисунка 7. Метки показывают токи в различных ветвях, найденные с использованием комбинации закона Ома и законов Кирхгофа . Резистор R ₁ = R _B // r _π1 и R ₃ = R _C2 // R _L . КВЛ от земли R ₁ к земле R ₂ обеспечивает:

$i_{\mathrm {B} }=-v_{\pi }{\frac {1+R_{2}/R_{1}+R_{\mathrm {f} }/R_{1}}{(\beta +1)R_{2}}}\ .$

КВЛ обеспечивает коллекторное напряжение на вершине R _C как

$v_{\mathrm {C} }=v_{\pi }\left(1+{\frac {R_{\mathrm {f} }}{R_{1}}}\right)-i_{\mathrm {B} }r_{\pi 2}\ .$

Наконец, KCL на этом коллекторе обеспечивает

$i_{\mathrm {T} }=i_{\mathrm {B} }-{\frac {v_{\mathrm {C} }}{R_{\mathrm {C} }}}\ .$

Подставляя первое уравнение во второе, а второе в третье, коэффициент возврата находится как

$T=-{\frac {i_{\mathrm {R} }}{i_{\mathrm {T} }}}=-g_{\mathrm {m} }{\frac {v_{\pi }}{i_{\mathrm {T} }}}$

$={\frac {g_{\mathrm {m} }R_{\mathrm {C} }}{\left(1+{\frac {R_{\mathrm {f} }}{R_{1}}}\right)\left(1+{\frac {R_{\mathrm {C} }+r_{\pi 2}}{(\beta +1)R_{2}}}\right)+{\frac {R_{\mathrm {C} }+r_{\pi 2}}{(\beta +1)R_{1}}}}}\ .$

Коэффициент усиления G ₀ при T = 0

Схема для определения G ₀ показана на центральной панели рисунка 7. На рисунке 7 выходной переменной является выходной ток β i _B (ток нагрузки короткого замыкания), который приводит к усилению тока короткого замыкания усилитель, а именно β i _B / i _S :

$G_{0}={\frac {\beta i_{B}}{i_{S}}}\ .$

Используя закон Ома , напряжение на вершине R ₁ находится как

$(i_{S}-i_{R})R_{1}=i_{R}R_{f}+v_{E}\ \ ,$

или, переставив термины,

$i_{S}=i_{R}\left(1+{\frac {R_{f}}{R_{1}}}\right)+{\frac {v_{E}}{R_{1}}}\ .$

Использование KCL в верхней части R ₂ :

$i_{R}={\frac {v_{E}}{R_{2}}}+(\beta +1)i_{B}\ .$

Напряжение эмиттера v _E уже известно через i _B из диаграммы на рисунке 7. Подставляя второе уравнение в первое, i _B определяется только через i _S , и G ₀ становится:

$G_{0}={\frac {\beta }{(\beta +1)\left(1+{\frac {R_{f}}{R_{1}}}\right)+(r_{\pi 2}+R_{C})\left[{\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\left(1+{\frac {R_{f}}{R_{1}}}\right)\right]}}$

Коэффициент усиления G ₀ представляет собой прямую связь через сеть обратной связи и обычно незначителен.

Выигрыш G _∞ при T → ∞

Схема для определения G _∞ показана на нижней панели рисунка 7. Введение идеального операционного усилителя (нулевого ) в эту схему объясняется следующим образом. При T → ∞ коэффициент усиления усилителя также стремится к бесконечности, и в таком случае дифференциальное напряжение, управляющее усилителем (напряжение на входном транзисторе r _π1 ), сводится к нулю и (согласно закону Ома при наличии нет напряжения) он не потребляет входной ток. С другой стороны, выходной ток и выходное напряжение соответствуют требованиям схемы. Такое поведение похоже на нуль, поэтому нуль можно ввести для обозначения транзистора с бесконечным коэффициентом усиления.

Текущее усиление считывается непосредственно со схемы:

$G_{\infty }={\frac {\beta i_{B}}{i_{S}}}=\left({\frac {\beta }{\beta +1}}\right)\left(1+{\frac {R_{f}}{R_{2}}}\right)\ .$

Сравнение с классической теорией обратной связи

В классической модели прямой связью пренебрегают, а коэффициент обратной связи β _FB составляет (при условии, что транзистор β >> 1):

$\beta _{FB}={\frac {1}{G_{\infty }}}\approx {\frac {1}{(1+{\frac {R_{f}}{R_{2}}})}}={\frac {R_{2}}{(R_{f}+R_{2})}}\ ,$

в разомкнутом контуре а коэффициент усиления A равен:

$A=G_{\infty }T\approx {\frac {\left(1+{\frac {R_{f}}{R_{2}}}\right)g_{m}R_{C}}{\left(1+{\frac {R_{f}}{R_{1}}}\right)\left(1+{\frac {R_{C}+r_{\pi 2}}{(\beta +1)R_{2}}}\right)+{\frac {R_{C}+r_{\pi 2}}{(\beta +1)R_{1}}}}}\ .$

Общий выигрыш

Приведенные выше выражения можно подставить в уравнение модели асимптотического усиления, чтобы найти общий коэффициент усиления G. Полученный коэффициент усиления представляет собой коэффициент усиления по току усилителя с нагрузкой короткого замыкания.

Выигрыш с использованием альтернативных выходных переменных

В усилителе, показанном на рисунке 6, RC2 _RL включены параллельно _​​и . Чтобы получить коэффициент усиления транссопротивления, скажем A _ρ , то есть коэффициент усиления, использующий напряжение в качестве выходной переменной, коэффициент усиления тока короткого замыкания G умножается на R _C2 // R _L в соответствии с законом Ома :

$A_{\rho }=G\left(R_{\mathrm {C2} }//R_{\mathrm {L} }\right)\ .$

Коэффициент усиления по напряжению холостого хода находится из A _ρ , установив R _L → ∞.

Чтобы получить коэффициент усиления по току, когда ток нагрузки i _L в нагрузочном резисторе является _RL выходной переменной, скажем A _i формула деления тока , используется : i _L = i _out × _RC2 / ( _RC2 + _RL ) и коэффициент усиления тока короткого замыкания G умножается на этот коэффициент нагрузки :

$A_{i}=G\left({\frac {R_{C2}}{R_{C2}+R_{L}}}\right)\ .$

Конечно, усиление тока короткого замыкания восстанавливается установкой R _L = 0 Ом.

См. также

• Теорема Блэкмана
• Теорема о дополнительном элементе
• Формула выигрыша Мейсона
• Усилители обратной связи
• Коэффициент возврата
• График потока сигналов

Внешние ссылки

• Конспект лекций по модели асимптотического усиления