Целочисленный многогранник

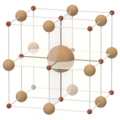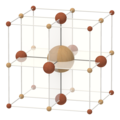Четыре целых многогранника в трех измерениях


Куб	Кубооктаэдр	Октаэдр	Усечено октаэдр
(±1, ±1, ±1)	(0, ±1, ±1)	(0, 0, ±1)	(0, ±1, ±2)

В геометрии и многогранной комбинаторике целым многогранником называется выпуклый многогранник, которого все вершины имеют целые декартовы координаты . ^[1] То есть это многогранник, равный выпуклой оболочке его целых точек . ^[2]Целочисленные многогранники также называются решетчатыми многогранниками или Z-многогранниками . Частные случаи двумерных и трехмерных целочисленных многогранников можно называть многоугольниками или многогранниками вместо многогранников соответственно.

Примеры [ править ]

Ан $n$ -мерный правильный симплекс можно представить в виде целочисленного многогранника в $\mathbb {R} ^{n+1}$ , выпуклая оболочка целочисленных точек, для которых одна координата равна единице, а остальные равны нулю. Другой важный тип целочисленного симплекса, ортосхема , может быть сформирован как выпуклая оболочка целых точек, координаты которых начинаются с некоторого количества последовательных единиц, за которыми следуют нули во всех остальных координатах. $n$ -мерный единичный куб в $\mathbb {R} ^{n}$ имеет вершинами все целые точки, координаты которых равны нулю или единице. Пермутаэдр имеет вершины , координаты которых получаются применением всех возможных перестановок к вектору $(1,2,...,n)$ . Ассоциэдр в выпуклой реализации Лодея также является целочисленным многогранником и деформацией пермутаэдра.

В оптимизации [ править ]

В контексте линейного программирования и связанных с ним задач математической оптимизации выпуклые многогранники часто описываются системой линейных неравенств , которым должны подчиняться их точки. Когда многогранник является целочисленным, линейное программирование можно использовать для решения задач целочисленного программирования для данной системы неравенств, проблема, которая в противном случае может быть более сложной.

Некоторые многогранники, возникающие в результате задач комбинаторной оптимизации, автоматически являются целыми. Например, это верно для порядкового многогранника любого частично упорядоченного множества , многогранника, определяемого парными неравенствами между координатами, соответствующими сравнимым элементам набора. ^[3]Другой известный многогранник в комбинаторной оптимизации — это совпадающий многогранник . Очевидно, что поиск паросочетаний осуществляется алгоритмически, и одним из методов является линейное программирование. Многогранник, описываемый линейной программой, ограничивающей сверху сумму ребер, взятых на одну вершину, является целым в случае двудольных графов , то есть точно описывает соответствующий многогранник, тогда как для общих графов он нецелочислен. ^[4]Следовательно, для двудольных графов достаточно решить соответствующую линейную программу, чтобы получить допустимое паросочетание . Однако для общих графов существуют две другие характеристики соответствующего многогранника, одна из которых использует неравенство Блума для нечетных подмножеств вершин и, следовательно, позволяет преобразовать целочисленную программу в линейную, сохраняя при этом действительные сопоставления. ^[5] Эти характеристики представляют дополнительный интерес для знаменитого алгоритма Блума Эдмондса, используемого для поиска таких паросочетаний в общих графах.

Вычислительная сложность [ править ]

Для многогранника, описываемого линейными неравенствами, если многогранник нецелый, его нецелостность можно доказать, найдя вершину, координаты которой не являются целыми числами. Такую вершину можно описать комбинаторно, задав подмножество неравенств, которые при преобразовании в систему линейных уравнений имеют единственное решение, и проверив, что эта точка решения подчиняется всем остальным неравенствам. Таким образом, проверка целостности относится к классу сложности задач coNP , для которых можно легко доказать отрицательный ответ. Точнее, он coNP-полный . ^[6]

Связанные объекты [ править ]

Многие важные свойства целочисленного многогранника, включая его объем и количество вершин, кодируются его полиномом Эрхарта . ^[7]

Целочисленные многогранники занимают видное место в теории торических многообразий , где они соответствуют поляризованным проективным торическим многообразиям. Например, торическое многообразие, соответствующее симплексу, является проективным пространством . Торическое многообразие, соответствующее единичному кубу , представляет собой вложение Сегре $n$ -кратное произведение проективной прямой. ^{[ нужна цитата ]}

В алгебраической геометрии важным примером решетчатых многогранников, называемых многогранниками Ньютона , являются выпуклые оболочки векторов, представляющих показатели степени каждой переменной в терминах многочлена . Например, полином $xy+2x^{2}+y^{5}+4$ имеет четыре члена, $xy$ с вектором экспоненты (1,1), $2x^{2}$ с вектором показателя (2,0), $y^{5}$ с вектором экспоненты (0,5) и $4$ с вектором показателя (0,0). Его многогранник Ньютона представляет собой выпуклую оболочку четырех точек (1,1), (2,0), (0,5) и (0,0). Эта оболочка представляет собой цельный треугольник с точкой (1,1) внутри треугольника и тремя другими точками в качестве его вершин.

См. также [ править ]

Рив тетраэдр

Ссылки [ править ]

^ Корнюжоль, Жерар (2001), Комбинаторная оптимизация: упаковка и покрытие , Серия региональных конференций CBMS-NSF по прикладной математике, том. 74, Филадельфия, Пенсильвания: Общество промышленной и прикладной математики (SIAM), стр. 74. 4, номер домена : 10.1137/1.9780898717105 , ISBN 0-89871-481-8 , МР 1828452
^ Мурота, Кадзуо (2003), Дискретный выпуклый анализ , Монографии SIAM по дискретной математике и приложениям, Филадельфия, Пенсильвания: Общество промышленной и прикладной математики (SIAM), стр. 90, doi : 10.1137/1.9780898718508 , hdl : 2433/149564 , ISBN 0-89871-540-7 , г.р. 1997998
^ Стэнли, Ричард П. (1986), «Два упорядоченных многогранника», Дискретная и вычислительная геометрия , 1 (1): 9–23, doi : 10.1007/BF02187680 , MR 0824105
^ Ловаш, Ласло (1986). Теория соответствия . Северная Голландия. стр. 269–274. ISBN 978-0-444-87916-5 . OCLC 316569965 .
^ Ловас, Ласло (1986). Теория соответствия . Северная Голландия. стр. 274–281. ISBN 978-0-444-87916-5 . OCLC 316569965 .
^ Дин, Гуоли; Фэн, Ли; Занг, Вэнань (2008), «Сложность распознавания линейных систем с определенными свойствами целостности», Mathematical Programming, Series A , 114 (2): 321–334, doi : 10.1007/s10107-007-0103-y , hdl : 10722 /58972 , МР 2393045
^ Барвинок, А.И. (1994), "Вычисление полинома Эрхарта выпуклого решетчатого многогранника", Дискретная и вычислительная геометрия , 12 (1): 35–48, doi : 10.1007/BF02574364 , MR 1280575

[c-1] Корнюжоль, Жерар (2001), Комбинаторная оптимизация: упаковка и покрытие , Серия региональных конференций CBMS-NSF по прикладной математике, том. 74, Филадельфия, Пенсильвания: Общество промышленной и прикладной математики (SIAM), стр. 74. 4, номер домена : 10.1137/1.9780898717105 , ISBN 0-89871-481-8 , МР 1828452

[m-2] Мурота, Кадзуо (2003), Дискретный выпуклый анализ , Монографии SIAM по дискретной математике и приложениям, Филадельфия, Пенсильвания: Общество промышленной и прикладной математики (SIAM), стр. 90, doi : 10.1137/1.9780898718508 , hdl : 2433/149564 , ISBN 0-89871-540-7 , г.р. 1997998

[s-3] Стэнли, Ричард П. (1986), «Два упорядоченных многогранника», Дискретная и вычислительная геометрия , 1 (1): 9–23, doi : 10.1007/BF02187680 , MR 0824105

[4] Ловаш, Ласло (1986). Теория соответствия . Северная Голландия. стр. 269–274. ISBN 978-0-444-87916-5 . OCLC 316569965 .

[5] Ловас, Ласло (1986). Теория соответствия . Северная Голландия. стр. 274–281. ISBN 978-0-444-87916-5 . OCLC 316569965 .

[dfz-6] Дин, Гуоли; Фэн, Ли; Занг, Вэнань (2008), «Сложность распознавания линейных систем с определенными свойствами целостности», Mathematical Programming, Series A , 114 (2): 321–334, doi : 10.1007/s10107-007-0103-y , hdl : 10722 /58972 , МР 2393045

[b-7] Барвинок, А.И. (1994), "Вычисление полинома Эрхарта выпуклого решетчатого многогранника", Дискретная и вычислительная геометрия , 12 (1): 35–48, doi : 10.1007/BF02574364 , MR 1280575

[1]

[2]

[3]

[4]

[5]

[6]

[7]