Пермутоэдр

Пермутоэдр четвертого порядка

В математике пермутоэдр пермутаэдр (также называемый , ) порядка n — это ( n — 1)-мерный многогранник вложенный в n -мерное пространство. Координаты его вершин (метки) представляют собой перестановки первых n натуральных чисел . Ребра определяют кратчайшие возможные пути (наборы транспозиций ), соединяющие две вершины (перестановки). Две перестановки, соединенные ребром, отличаются только в двух местах (одна транспозиция ), а числа на этих местах являются соседями (отличаются по значению на 1).

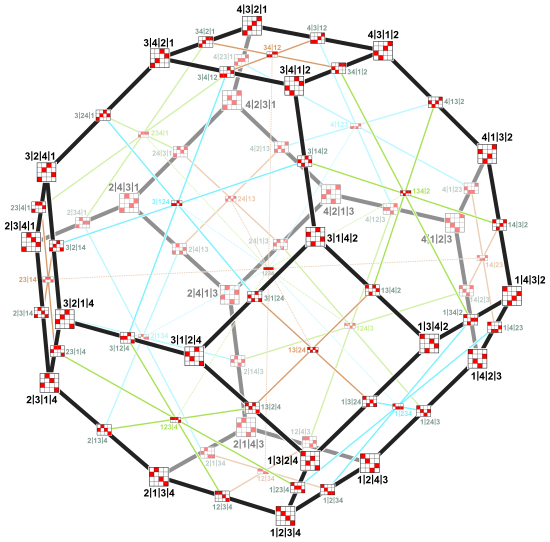
На изображении справа показан пермутоэдр четвертого порядка, который представляет собой усеченный октаэдр . Его вершинами являются 24 перестановки (1, 2, 3, 4). Параллельные края имеют одинаковый цвет. 6 цветов ребер соответствуют 6 возможным транспозициям 4 элементов, т.е. они указывают, в каких двух местах соединенные перестановки различаются. (Например, красные ребра соединяют перестановки, которые отличаются в двух последних местах.)

История

По словам Гюнтера М. Циглера ( 1995 ), пермутоэдры были впервые изучены Питером Хендриком Шауте ( 1911 ). Название пермутоэдр было придумано Жоржем Т. Гильбо и Пьер Розенштиль ( 1963 ). Они описывают это слово как варварское, но легко запоминающееся, и подвергают его критике со стороны читателей.

альтернативное написание перестановка эдра . Иногда также используется Пермутоэдры иногда называют многогранниками перестановок , но эта терминология также используется для родственного многогранника Биркгофа , определяемого как выпуклая оболочка матриц перестановок . В более общем смысле, В. Джозеф Боуман ( 1972 ) использует этот термин для любого многогранника, вершины которого имеют биекцию с перестановками некоторого множества.

Вершины, ребра и грани

вершины , края , грани , лица Размер лица d знак равно n - k .

k = 1 2 3 4 5n1 1 12 1 2 33 1 6 6 134 1 14 36 24 755 1 30 150 240 120 541

Пермутоэдр порядка n имеет n ! вершин, каждая из которых смежна с n − 1 другими.Количество ребер ⁠ ( п - 1) п ! / 2 ⁠ , а их длина равна √ 2 .

Две связанные вершины отличаются заменой двух координат, значения которых отличаются на 1. Пара перепутанных мест соответствует направлению ребра.(В примере изображения вершины (3, 2, 1, 4) и (2, 3, 1, 4) соединены синим краем и отличаются заменой 2 и 3 в первых двух местах. Значения 2 и 3 отличаются на 1. Все синие ребра соответствуют перестановкам координат на первых двух местах.)

Количество граней 2 . ^н − 2 , поскольку они соответствуют непустым собственным подмножествам S из {1 ... n } . вершин фасета, соответствующего подмножеству S Общим для , является то, что их координаты в местах S меньше остальных .

showПримеры фасетов
For order 3 the facets are the 6 edges, and for order 4 they are the 14 faces. The coordinates on places i where i ∈ S are marked with a dark background. It can be seen, that they are smaller than the rest. The square on top corresponds to the subset {3, 4}. In its four vertices the coordinates on the last two places have the smallest values (namely 1 and 2).
order 3		order 4
1-element subsets	2-element subsets	1-element subsets	2-element subsets	3-element subsets

В более общем смысле, грани размерностей от 0 (вершины) до n - 1 (сам пермутоэдр) соответствуют строгим слабым порядкам набора {1 ... n } . Таким образом, количество всех граней — это n -е упорядоченное число Белла . Грань размерности d соответствует порядку с классами эквивалентности k = n − d .

showПримеры лиц
order 3	order 4
The images above show the face lattices of the permutohedra of order 3 and 4 (without the empty faces). Each face center is labelled with a strict weak ordering.E.g. the square on top as 3 4 | 1 2, which represents ({3, 4}, {1, 2}). The orderings are partially ordered by refinement, with the finer ones being on the outside. Moving along an edge toward the inside means merging two neighbouring equivalence classes. The vertex labels a | b | c | d interpreted as permutations (a, b, c, d) are those forming the Cayley graph. showFacets among the faces The before mentioned facets are among these faces, and correspond to orderings with two equivalence classes. The first one is used as the subset S assigned to the facet, so the ordering is (S, Sc). The images below show how the facets of the n-permutohedron correspond to the simplical projection of the n-cube. The binary coordinate labels correspond to the subsets S, e.g. 0011 to {3, 4}. (The vertex projected to the center does not correspond to a facet. Nor does its opposite vertex in the n-cube, which is not part of the projection.)

Число граней размерности d = n − k в пермутоэдре порядка n задается треугольником T (последовательность A019538 в OEIS ):
$T(n,k)=k!\cdot \left\{{n \atop k}\right\}$ с $\textstyle \left\{{n \atop k}\right\}$ представляющие числа Стирлинга второго рода
Оно показано справа вместе с суммами строк — упорядоченными числами Белла .

Другие объекты недвижимости

Подобный пермутоэдру граф Кэли S ₄ ( см. здесь ) сравнение с пермутоэдром

Пермутоэдр вершинно-транзитивен действует на пермутоэдр _{: симметрическая группа Sn} перестановкой координат.

Пермутоэдр — это зонотоп ; переведенная копия пермутоэдра может быть сгенерирована как сумма Минковского отрезков прямых n ( n - 1)/2 , которые соединяют пары стандартных базисных векторов.

Вершины и ребра пермутоэдра изоморфны одному из графов Кэли , симметрической группы а именно тому, который порождается транспозициями , меняющими местами последовательные элементы. Вершины графа Кэли являются обратными перестановками вершин пермутоэдра. Изображение справа показывает график Кэли S 4 . Цвета его краев представляют собой 3 порождающие транспозиции: (1, 2) , (2, 3) , (3, 4)

Этот граф Кэли является гамильтоновым ; гамильтонов цикл можно найти с помощью алгоритма Штейнхауса-Джонсона-Троттера .

Тесселяция пространства

Тесселяция пространства пермутоэдрами третьего и четвертого порядков.

Пермутоэдр порядка n целиком лежит в ( n − 1 )-мерной гиперплоскости, состоящей из всех точек, сумма координат которых равна числу

1 + 2 + ... + n = n ( n + 1)/2.

Более того, эту гиперплоскость можно замостить бесконечным количеством переведенных копий пермутоэдра. Каждый из них отличается от базового пермутоэдра элементом некоторой ( n − 1)-мерной решетки , которая состоит из n -кортежей целых чисел, сумма которых равна нулю и все вычеты которых (по модулю n ) равны:

х ₁ + х ₂ + ... + х _n = 0

Икс ₁ ≡ Икс ₂ ≡ ... ≡ Икс _п (по модулю п ).

Это решетка $A_{n-1}^{*}$, двойственная решетка корневой решетки $A_{n-1}$. Другими словами, пермутоэдр — это ячейка Вороного для $A_{n-1}^{*}$. Соответственно эту решетку иногда называют пермутоэдрической решеткой.

Таким образом, показанный выше пермутоэдр 4-го порядка замощает трехмерное пространство путем перемещения. Здесь трехмерное пространство — это аффинное подпространство четырехмерного пространства R ⁴ с координатами x , y , z , w, который состоит из четырех наборов действительных чисел, сумма которых равна 10,

х + у + г + ш = 10.

Легко проверить, что для каждого из следующих четырех векторов

(1,1,1,−3), (1,1,−3,1), (1,−3,1,1) и (−3,1,1,1),

сумма координат равна нулю, и все координаты конгруэнтны 1 (по модулю 4). Любые три из этих векторов образуют решетку трансляции.

Тесселяции, образованные таким образом из пермутоэдров второго, третьего и четвертого порядка соответственно, представляют собой апейрогон , правильную шестиугольную мозаику и кубическую соту с усеченными кусочками . Двойные мозаики содержат все симплексные грани, хотя они не являются правильными многогранниками выше третьего порядка.

Примеры

Заказ 2	Заказ 3	Заказ 4	Заказать 5	Заказ 6
2 вершины	6 вершин	24 вершины	120 вершин	720 вершин
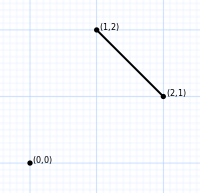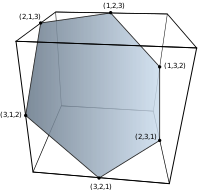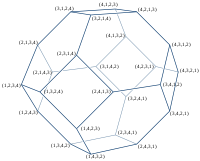сегмент линии	шестиугольник	усеченный октаэдр	всеусеченный 5-клеточный	всеусеченный 5-симплекс

См. также

• Ассоциэдр
• Циклоэдр
• Пермутоассоциэдр

Ссылки

• Пэк, Чонмин; Адамс, Эндрю; Долсон, Дженнифер (2013), «Высокоразмерная гауссова фильтрация на основе решетки и пермутоэдральная решетка», Journal of Mathematical Imaging and Vision , 46 (2): 211–237, doi : 10.1007/s10851-012-0379-2 , HDL : 1721.1/105344 , МР   3061550
• Боуман, В. Джозеф (1972), «Многогранники перестановок», SIAM Journal on Applied Mathematics , 22 (4): 580–589, doi : 10.1137/0122054 , JSTOR   2099695 , MR   0305800 .
• Гаиха, Прабха; Гупта, С.К. (1977), «Смежные вершины пермутоэдра», SIAM Journal on Applied Mathematics , 32 (2): 323–327, doi : 10.1137/0132025 , JSTOR   2100417 , MR   0427102 .
• Гильбо, Жорж Т.; Розенштиль, Пьер (1963), «Алгебраический анализ избирательного бюллетеня» , Mathematics and Human Sciences , 4 : 9–33 .
• Лансия, Джузеппе (2018), Компактные модели расширенного линейного программирования , Чам, Швейцария: Springer, ISBN  978-3-319-63975-8 .
• Шуте, Питер Хендрик (1911), «Аналитическая обработка многогранников, регулярно полученных из правильных многогранников», Трактаты Королевской академии искусств и наук в Амстердаме , 11 (3): 87 стр. Googlebook, 370–381 Также онлайн на сайте Цифровая библиотека KNAW по адресу http://www.dwc.knaw.nl/accessen/digital-library-knaw/?pagetype=publDetail&pId=PU00011495.
• Томас, Рекха Р. (2006), «Глава 9. Пермутаэдр», Лекции по геометрической комбинаторике , Студенческая математическая библиотека: IAS / Park City Mathematical Subseries, vol. 33, Американское математическое общество , стр. 85–92, ISBN.  978-0-8218-4140-2 .
• Циглер, Гюнтер М. (1995), Лекции по многогранникам , Springer-Verlag, Тексты для аспирантов по математике 152 .

Дальнейшее чтение

• Ле Конте де Поли-Барбю, Кл. (1990), «Диаграмма решетки пермутоэдров представляет собой пересечение диаграмм двух прямых произведений полных порядков», Mathematics, Computer Science and Human Sciences , 112 : 49–53 .
• Постников, Александр (2009), «Пермутоэдры, ассоциэдры и не только», Международные уведомления о математических исследованиях , 2009 (6): 1026–1106, arXiv : math.CO/0507163 , doi : 10.1093/imrn/rnn153 , MR   2487491
• Сантмайер, Джо (2007), «Для всех возможных расстояний посмотрите на пермутоэдр», Mathematics Magazine , 80 (2): 120–125, doi : 10.1080/0025570X.2007.11953465

Внешние ссылки

• Брайан Джейкобс, «Пермутоэдр» , MathWorld