Гипотеза об одиноком бегуне

Нерешенная задача по математике :

Верна ли гипотеза одинокого бегуна для любого количества бегунов?

(еще нерешенные задачи по математике)

В теории чисел , в частности, в изучении диофантовой аппроксимации , гипотеза одинокого бегуна — это гипотеза о долгосрочном поведении бегунов на круговой дорожке. В нем говорится, что $n$ бегуны на беговой дорожке единичной длины, с постоянными скоростями, отличными друг от друга, каждый в какой-то момент будет одинок — по крайней мере $1/n$ единицы вдали от всех остальных.

Гипотеза была впервые сформулирована в 1967 году немецким математиком Йоргом М. Уиллсом в чисто теоретико-числовых терминах и независимо в 1974 году Т.В. Кьюзиком; ее наглядная и сейчас популярная формулировка датируется 1998 годом. Известно, что эта гипотеза верна для семи бегунов или меньше, но общий случай остается нерешенным. Последствия гипотезы включают решения проблем с препятствиями для просмотра и оценки свойств, связанных с хроматическими числами , некоторых графов.

Формулировка

Пример случая гипотезы с n =6 бегунами. Бегуны, окрашенные в черный цвет, еще не были одиноки. Белые дуги длиной 2/ n обозначают, что бегун в данный момент одинок. Желтые бегуны испытали одиночество.

Учитывать $n$ бегуны на круговой дорожке единичной длины. В начальный момент $t=0$, все бегуны находятся в одном положении и начинают бежать; скорости бегунов постоянны, все различны и могут быть отрицательными. Говорят, что бегун бывает одинок временами $t$ если они находятся на расстоянии (измеренном по окружности) не менее $1/n$ от каждого второго бегуна. Гипотеза одинокого бегуна утверждает, что каждый бегун в какое-то время одинок, независимо от выбора скорости.

Эта визуальная формулировка гипотезы была впервые опубликована в 1998 году. Во многих формулировках, включая оригинал Йорга М. Уиллса, сделаны некоторые упрощения. Бегун, которому будет одиноко, неподвижен в точке 0 (с нулевой скоростью), и, следовательно, $n-1$ учитываются другие бегуны с ненулевой скоростью. Движущиеся бегунки могут быть ограничены только положительными скоростями: по симметрии бегуны со скоростями $x$ и $-x$ всегда находятся на одинаковом расстоянии от 0 и поэтому по существу эквивалентны. Доказательство результата для любого бегуна, стоящего на месте, подразумевает общий результат для всех бегунов, поскольку их можно сделать неподвижными, вычитая их скорость из скорости всех бегунов, оставляя их с нулевой скоростью. Гипотеза затем утверждает, что для любого набора $v_{1},v_{2},...,v_{n-1}$ положительных, различных скоростей, существует некоторое время $t>0$ такой, что $${\frac {1}{n}}\leq \operatorname {frac} (v_{i}t)\leq 1-{\frac {1}{n}}\qquad (i=1,...,n-1),$$где $\operatorname {frac} (x)$ обозначает часть дробную $x$. Визуально интерпретируется следующим образом: если бегуны бегут против часовой стрелки, средний член неравенства — это расстояние от начала координат до точки. $i$й бегун на данный момент $t$, измеренное против часовой стрелки. Это соглашение используется в оставшейся части этой статьи. Гипотеза Уиллса была частью его работы по диофантовому приближению . изучение того, насколько близко дроби могут приближаться к иррациональным числам.

Подразумеваемое

Квадраты со стороной 1/3, расположенные в каждой полуцелой координате, загораживают любой луч из начала координат (кроме лежащих на оси). Любая меньшая длина стороны оставит небольшие зазоры.

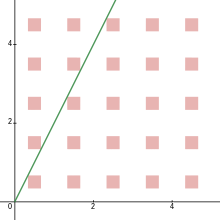
Предполагать $C$ представляет собой n - гиперкуб с длиной стороны $s$ в n -мерном пространстве ( $n\geq 2$). Поместите центрированную копию $C$ в каждой точке с полуцелыми координатами. Луч из начала координат может либо пропустить все копии $C$, и в этом случае существует (бесконечно малый) пробел или попадание хотя бы в одну копию. Кьюсик (1973) в этом контексте сформулировал независимую гипотезу об одиноком бегуне; из гипотезы следует, что пробелы существуют тогда и только тогда, когда $s<(n-1)/(n+1)$, игнорируя лучи, лежащие в одной из координатных гиперплоскостей. Например, в двухмерном пространстве квадраты размером меньше $1/3$ по длине стороны останутся пробелы, как показано, и квадраты с длиной стороны. $1/3$ или больше будет препятствовать каждому лучу, который не параллелен оси. Гипотеза обобщает это наблюдение на любое количество измерений.

В теории графов дистанционный граф $G$ на множестве целых чисел и используя некоторое конечное множество $D$ положительных целых расстояний, имеет ребро между $x,y$ тогда и только тогда, когда $|x-y|\in D$. Например, если $D=\{2\}$, каждая последовательная пара четных целых чисел и нечетных целых чисел является смежной, и все вместе они образуют два связных компонента . A k - регулярная раскраска целых чисел с шагом $\lambda \in \mathbb {R}$ присваивает каждому целому числу $n$ один из $k$ цвета на остатков основе $\lfloor \lambda n\rfloor$модуль $k$. Например, если $\lambda =0.5$, раскраска повторяется каждые $2k$ целые числа и каждая пара целых чисел $2m,2m+1$ одного цвета. принимая $k=|D|+1$, гипотеза одинокого бегуна подразумевает $G$ допускает правильную k -регулярную раскраску (т. е. каждый узел раскрашен иначе, чем его соседи) для некоторого значения шага. Например, $(k,\lambda )=(2,0.5)$ генерирует правильную раскраску на графе расстояний, сгенерированном $D=\{2\}$. ( $k$ известно как регулярное хроматическое число $D$.)

Учитывая ориентированный граф $G$, ненулевой поток нигде $G$ ассоциируется с положительным значением $f(e)$ к каждому краю $e$, так что поток наружу из каждого узла равен потоку внутрь. Гипотеза одинокого бегуна подразумевает, что если $G$ имеет нигде ненулевой поток с не более чем $k$ различные целочисленные значения, тогда $G$ имеет нигде ненулевой поток со значениями только в $\{1,2,\ldots ,k\}$ (возможно, после изменения направления некоторых дуг $G$). Этот результат был доказан для $k\geq 5$ с помощью отдельных методов, а поскольку меньшие случаи гипотезы одинокого бегуна решены, полная теорема доказана.

Известные результаты

Для данной настройки бегунов пусть $\delta$ обозначают наименьшую из максимальных дистанций одиночества бегунов и разрыв одиночества $\delta _{n}$ обозначаем минимум $\delta$ во всех установках с $n$ бегуны. В этих обозначениях гипотеза утверждает, что $\delta _{n}\geq 1/n$, граница, которая, если она верна, не может быть улучшена. Например, если бегун, которому предстоит быть одиноким, стоит на месте и ускоряется $v_{i}=i$ выбраны, то не существует момента времени, когда они строго больше $1/n$ единиц от всех остальных, показывая, что $\delta _{n}\leq 1/n$. В качестве альтернативы этот вывод можно быстро вывести из аппроксимационной теоремы Дирихле . Для $n\geq 2$ простая нижняя граница $\delta _{n}\geq 1/(2n-2)$ может быть получено с помощью вероятностного аргумента.

Гипотезу можно свести к ограничению скорости бегунов целыми положительными числами: если гипотеза верна для $n$ бегунов с целыми скоростями, это верно для $n$ бегуны с реальной скоростью.

Более жесткие границы

Небольшие улучшения нижней границы $1/(2n-2)$ известны. Чен и Кьюсик (1999) показали $n\geq 5$ что если $2n-5$ является простым, то $\delta _{n}\geq {\tfrac {1}{2n-5}}$, и если $4n-9$ является простым, то $\delta _{n}\geq {\tfrac {2}{4n-9}}$. Перарнау и Серра (2016) показали безоговорочно для достаточно больших $n$ что $$\delta _{n}\geq {\frac {1}{2n-4+o(1)}}.$$

Тао (2018) доказал самый известный на данный момент асимптотический результат: для достаточно больших $n$, $$\delta _{n}\geq {\frac {1}{2n-2}}+{\frac {c\log n}{n^{2}(\log \log n)^{2}}}$$для некоторой константы $c>0$. Он также показал, что полная гипотеза подразумевается, доказав гипотезу для целочисленных скоростей размера $n^{O(n^{2})}$ (см. большое обозначение O ). Это импликация теоретически позволяет доказать гипотезу для заданного $n$ путем проверки конечного набора случаев, но число случаев растет слишком быстро, чтобы это было практично.

Гипотеза была доказана при конкретных предположениях о скорости бегунов. Для достаточно большого $n$, это справедливо, если $${\frac {v_{i+1}}{v_{i}}}\geq 1+{\frac {22\log(n-1)}{n-1}}\qquad (i=1,...,n-2).$$Другими словами, гипотеза справедлива для больших $n$ если скорости растут достаточно быстро. Если константу 22 заменить на 33, то гипотеза верна для $n\geq 16343$. Аналогичный результат для достаточно больших $n$ требуется только аналогичное предположение для $i=\lfloor n/22\rfloor -1,...,n-2$. Безоговорочно включено $n$, гипотеза верна, если $v_{i+1}/v_{i}\geq 2$ для всех $i$.

Для конкретного n

Гипотеза верна для $n\leq 7$ бегуны. Доказательства для $n\leq 3$ являются элементарными; тот $n=4$ Дело было возбуждено в 1972 году. $n=5$, $n=6$, и $n=7$ дела были урегулированы в 1984, 2001 и 2008 годах соответственно. Первое доказательство для $n=5$ было проведено с помощью компьютера, но с тех пор все случаи были доказаны элементарными методами.

Для некоторых $n$существуют спорадические примеры с максимальным разделением $1/n$ помимо примера $v_{i}=i$ приведено выше. Для $n=5$, единственный известный пример (с точностью до сдвигов и масштабирования) — это $\{0,1,3,4,7\}$; для $n=6$ единственный известный пример $\{0,1,3,4,5,9\}$; и для $n=8$ известные примеры $\{0,1,4,5,6,7,11,13\}$ и $\{0,1,2,3,4,5,7,12\}$. Существует явное бесконечное семейство таких спорадических случаев.

Кравиц (2021) сформулировал более точную версию гипотезы, касающуюся случаев, близких к равенству. Более конкретно, он предполагает, что для данного набора скоростей $v_{i}$, или $\delta =s/(s(n-1)+1)$ для некоторого положительного целого числа $s$, или $\delta \geq 1/(n-1)$, где $\delta$ это разрыв одиночества в этой установке. Он подтвердил эту гипотезу для $n\leq 4$ и несколько особых случаев.

Риффорд (2022) обратился к вопросу о том, сколько времени требуется бегуну, чтобы почувствовать себя одиноким. Он сформулировал более сильную гипотезу, утверждающую, что для любого целого числа $n\geq 3$ есть целое положительное число $N$ такой, что для любой коллекции $v_{1},v_{2},...,v_{n-1}$ положительных, различных скоростей, существует некоторое время $t>0$ такой, что $\operatorname {frac} (v_{i}t)\in [1/n,1-1/n]$ для $i=1,...n-1$ с $$t\leq {\frac {N}{\operatorname {min} (v_{1},...,v_{n-1})}}.$$Риффорд подтвердил эту гипотезу $n=3,4,5,6$ и показал, что минимальная $N$ в каждом случае определяется $N=1$ для $n=3,4,5$ и $N=2$ для $n=6$. Последний результат ( $N=2$ для $n=6$) показывает, что если мы рассмотрим шесть бегунов, начиная с $0$ во время $t=0$ с постоянной скоростью $v_{0},v_{1},...,v_{5}$ с $v_{0}=0$и $v_{1},...,v_{5}$ различим и положителен, то статический бегун находится на расстоянии не менее $1/6$ от остальных в течение первых двух раундов самого медленного нестатичного бегуна (но не обязательно в первом раунде).

Другие результаты

Гораздо более сильный результат существует для случайно выбранных скоростей: использование соглашения о стационарном бегуне, если $n$ и $\varepsilon >0$ фиксированы и $n-1$ бегуны с ненулевыми скоростями выбираются равномерно случайным образом из $\{1,2,\ldots ,k\}$, затем $P(\delta \geq 1/2-\varepsilon )\to 1$ как $k\to \infty$. Другими словами, бегуны со случайной скоростью, скорее всего, в какой-то момент окажутся «очень одинокими» — почти $1/2$ единиц от ближайшего другого бегуна. Полная гипотеза верна, если «одиночество» заменить на «почти одиночество», что означает, что не более одного бегуна находится внутри. $1/n$ данного бегуна. Гипотеза была обобщена до аналога в полях алгебраических функций .

Примечания и ссылки

Цитируемые работы

• Барахас, Хавьер; Серра, Ориол (2008a). «Одинокий бегун с семью бегунами» . Электронный журнал комбинаторики . 15 (1): Р48. дои : 10.37236/772 .
• ——; —— (сентябрь 2009 г.). «О хроматическом числе циркулянтных графов» . Дискретная математика . 309 (18): 5687–5696. дои : 10.1016/j.disc.2008.04.041 .
• Бетке, У.; Уиллс, Дж. М. (1972). «Нижние оценки для двух функций диофантовой аппроксимации». Ежемесячные журналы по математике . 76 (3): 214. doi : 10.1007/BF01322924 . S2CID   122549668 .
• Биения, Войцех; Годдин, Луис; Гвоздяк, Павол; Себё, Андраш; Тарси, Майкл (январь 1998 г.). «Потоки, препятствия обзора и одинокий бегун» . Журнал комбинаторной теории, серия B. 72 (1): 1–9. дои : 10.1006/jctb.1997.1770 .
• Боман, Том ; Хольцман, Рон; Клейтман, Дэн (февраль 2001 г.). «Шесть одиноких бегунов» . Электронный журнал комбинаторики . 8 (2): Р3. дои : 10.37236/1602 .
• Чен, Юн-Гао; Кьюсик, Т.В. (январь 1999 г.). «Проблема препятствия обзору для n-мерных кубов» . Журнал теории чисел . 74 (1): 126–133. дои : 10.1006/jnth.1998.2309 .
• Чоу, Сэм; Риманич, Лука (январь 2019 г.). «Одинокие бегуны в функциональных полях» (PDF) . Математика . 65 (3): 677–701. дои : 10.1112/S002557931900007X . S2CID   118621899 .
• Кьюсик, TW (1973). «Проблемы с затруднением обзора». Математические уравнения . 9 (2–3): 165–170. дои : 10.1007/BF01832623 . S2CID   122050409 .
• —— (1974). «Проблемы с препятствиями для просмотра в n-мерной геометрии» . Журнал комбинаторной теории, серия А. 16 (1): 1–11. дои : 10.1016/0097-3165(74)90066-1 .
• ——; Померанс, Карл (1984). «Проблемы с затруднением обзора, III» . Журнал теории чисел . 19 (2): 131–139. дои : 10.1016/0022-314X(84)90097-0 .
• Червинский, Себастьян (2012). «Случайные бегуны очень одиноки». Журнал комбинаторной теории, серия А. 119 (6): 1194–1199. arXiv : 1102.4464 . дои : 10.1016/j.jcta.2012.02.002 . S2CID   26415692 .
• —— (май 2018 г.). «Задача одинокого бегуна для лакунарных последовательностей» . Дискретная математика . 341 (5): 1301–1306. дои : 10.1016/j.disc.2018.02.002 .
• ——; Гричук, Ярослав (сентябрь 2008 г.). «Невидимые бегуны в конечных полях». Письма об обработке информации . 108 (2): 64–67. дои : 10.1016/j.ipl.2008.03.019 .
• Дубицкас, А. (2011). «Проблема одинокого бегуна для многих бегунов» . Гласник Математики . 46 : 25–30. дои : 10.3336/gm.46.1.05 .
• Годдин, Л.; Вонг, Эрик Б. (2006). «Тяжелые случаи одинокого бегуна» (PDF) . Целые числа . 6 (А38) . Проверено 1 мая 2022 г.
• Кравиц, Н. (2021). «Едва одинокие бегуны и очень одинокие бегуны: изысканный подход к проблеме одинокого бегуна». Комбинаторная теория . 1 . arXiv : 1912.06034 . дои : 10.5070/C61055383 . S2CID   245100000 .
• Перарнау, Гиллем; Серра, Ориол (март 2016 г.). «Корреляция между бегунами и некоторые результаты по гипотезе одинокого бегуна» . Электронный журнал комбинаторики . 23 (1): 1,50 песо. дои : 10.37236/5123 . S2CID   7039062 .
• Рено, Дж. (2004). «Препятствие для обзора: более короткое доказательство для шести одиноких бегунов» . Дискретная математика . 287 (1–3): 93–101. дои : 10.1016/j.disc.2004.06.008 .
• Риффорд, Л. (2022). «Когда бегуну станет одиноко» (PDF) . Acta Applicandae Mathematicae . 180 : Бумага № 15. doi : 10.1007/s10440-022-00515-9 .
• Тао, Теренс (31 декабря 2018 г.). «Некоторые замечания по поводу гипотезы одинокого бегуна» . Вклад в дискретную математику . 13 : № 2 (2018). дои : 10.11575/cdm.v13i2.62728 .
• Уиллс, Йорг М. (1967). «Две теоремы о неоднородной диофантовой аппроксимации иррациональных чисел». Ежемесячные журналы по математике . 71 (3): 263–269. дои : 10.1007/BF01298332 . S2CID   122754182 .

Внешние ссылки

• Статья в саду открытых проблем №. 4, 551–562.