Спектр чирпа

Спектр чирп -импульса описывает его характеристики с точки зрения его частотных составляющих. Это представление в частотной области является альтернативой более знакомой форме сигнала во временной области, и эти две версии математически связаны преобразованием Фурье . Спектр представляет особый интерес, когда импульсы подвергаются обработке . Например, когда ЛЧМ-импульс сжимается согласованным фильтром , результирующая форма сигнала содержит не только основной узкий импульс, но также и множество нежелательных артефактов, многие из которых напрямую связаны с особенностями спектральных характеристик ЛЧМ.

Простой способ получить спектр чирпа с помощью компьютера — это выполнить выборку формы сигнала во временной области на частоте, значительно превышающей предел Найквиста , и использовать алгоритм БПФ для получения желаемого результата. Поскольку этот подход не подходил первым проектировщикам, они прибегали к аналитическому анализу, графическим методам или методам аппроксимации. Однако эти ранние методы по-прежнему остаются полезными, поскольку дают дополнительную информацию о поведении и свойствах щебетаний.

Чирп-импульс

Общее выражение для колебательного сигнала с центром на частоте ω ₀ :

$s(t)=a(t)\cdot \exp[j(\omega _{0}\cdot t+\theta (t))]$

где $a(t)$ и θ (t) дают изменения амплитуды и фазы сигнала. $s$, со временем.
Частотный спектр этого сигнала получается путем расчета Фурье преобразования $s(t)$, то есть

$S(\omega )=\int _{-\infty }^{\infty }s(t)\cdot \exp(-j\omega t)\cdot dt=\int _{-\infty }^{\infty }a(t)\cdot \exp[j(\omega _{0}t+\theta (t))]\cdot \exp(-j\omega t)\cdot dt$
так
$S(\omega )=\int _{-\infty }^{\infty }a(t)\cdot \exp[j\left\{(\omega _{0}-\omega )\cdot t+\theta (t)\right\}]\cdot dt$

В некоторых особых случаях интеграл можно решить и получить аналитическое выражение , но часто характеристики $a(t)$ и θ (t) таковы, что интеграл можно оценить только с помощью аппроксимационного алгоритма или численного интегрирования .

Линейный чирп

В особом случае, когда s(t) ограничено импульсом с частотной модуляцией и плоской вершиной, мгновенная частота которого изменяется как линейная функция времени, тогда возможно аналитическое решение.

Для удобства считается, что импульс имеет единичную амплитуду и длительность T, причем амплитуда и фаза определяются в интервале времени от -T/2 до +T/2. Общая развертка частоты равна Δ F и изменяется линейным образом от - Δ F/2 до + Δ F/2 в определенном интервале времени.

Когда частота является линейной функцией времени, фаза является квадратичной функцией и s(t) можно записать

$s(t)=1\cdot \exp[j(\Delta \Omega \cdot t+{\frac {\Delta \Omega }{2T}}\cdot t^{2})]\qquad {\text{where}}\quad \Delta \Omega =2\pi \cdot \Delta F\qquad {\text{and}}\quad {\frac {-T}{2}}<t<{\frac {T}{2}}$

Спектр этого линейного FM-сигнала:

$S(\omega )=\int _{-T/2}^{T/2}\exp \left[j(\Delta \Omega \cdot t+{\frac {\Delta \Omega }{2T}}\cdot t^{2})\right]\cdot \exp(-j\omega \cdot t)\cdot dt=\int _{-T/2}^{T/2}\exp \left[j\left\{(\Delta \Omega -\omega )\cdot t+{\frac {\Delta \Omega }{2T}}\cdot t^{2}\right\}\right]\cdot dt$

Заполняя квадрат и используя интегралы Френеля C(X) и S(X), определяется

$C(X)=\int _{0}^{X}\cos {\frac {\pi \cdot y^{2}}{2}}\cdot dy\qquad {\text{and}}\qquad S(X)=\int _{0}^{X}\sin {\frac {\pi \cdot y^{2}}{2}}\cdot dy$

выражение можно оценить дать:

$S(\omega )={\sqrt {\left({\frac {\pi \cdot T}{\Delta \Omega }}\right)}}\cdot \exp \left[-j\left((\omega -\Delta \Omega )^{2}\cdot {\frac {T}{2\cdot \Delta \Omega }}\right)\right]\cdot [C(X_{1})+j\cdot S(X_{1})+C(X_{2})+j\cdot S(X_{2})]$

где $X_{1}$ и $X_{2}$ даны

$\quad X_{1}={\frac {{\frac {\Delta \Omega }{2}}+(\omega -\Delta \Omega )}{\sqrt {\frac {\pi \cdot \Delta \Omega }{T}}}}\quad {\text{and}}\quad X_{2}={\frac {{\frac {\Delta \Omega }{2}}+(\Delta \Omega -\omega )}{\sqrt {\frac {\pi \cdot \Delta \Omega }{T}}}}$

Можно считать, что линейный FM-спектр состоит из трех основных компонентов, а именно:

• Амплитудный член, $|S(\omega )|={\sqrt {\frac {\pi \cdot T}{\Delta \Omega }}}\cdot \left[\left(C(X_{1})+C(X_{2})\right)^{2}+\left(S(X_{1})+S(X_{2})\right)^{2}\right]^{\frac {1}{2}}$
• термин фазы квадратичного закона, $\quad -\Phi _{1}(\omega )=(\omega -\Delta \Omega )^{2}\cdot {\frac {T}{2\cdot \Delta \Omega }}$
• и срок остаточной фазы $\quad \Phi _{2}(\omega )=\arctan \left[{\frac {S(X_{1})+S(X_{2})}{C(X_{1})+C(X_{2})}}\right]$

Соотношение $\left[{\frac {S(X_{1})+S(X_{2})}{C(X_{1})+C(X_{2})}}\right]$ примерно равен единице в большей части интересующего диапазона частот, поэтому Φ ₂ здесь приближается к постоянному фазовому углу π /4. Если введен член масштабирования частоты n, где $n=2\cdot {\frac {(\omega -\omega _{0})}{\Delta \Omega }}$, то выражения для аргументов Френеля примут вид

$X_{1}={\frac {\sqrt {T\cdot \Delta F}}{\sqrt {2}}}\cdot (1+n)$ и

$X_{2}={\frac {\sqrt {T\cdot \Delta F}}{\sqrt {2}}}\cdot (1-n)$

Спектры теперь являются функциями произведения T. Δ F, независимо от каких-либо конкретных значений центральной частоты и полосы пропускания. Это произведение, T. Δ F, часто называют произведением частотной полосы пропускания чирпа.

Опубликованы таблицы интегралов Френеля. вместе с математическими программами, с помощью которых можно вычислять интегралы вручную или с помощью компьютерной программы. Кроме того, ряд математических программ, таких как Mathcad , MATLAB и Mathematica, имеют встроенные процедуры для вычисления интегралов либо в виде стандартных функций, либо в пакетах расширений.

Некоторые графики спектра мощности |S( ω )| ² показаны как функция частоты для произведений временной полосы 25, 100, 250 и 1000. Когда произведение мало, пульсации Френеля очень заметны, но спектр имеет тенденцию к более прямоугольному профилю для больших значений. .

В случае графиков остаточной фазы Φ 2( ω ) профили имеют тенденцию быть очень похожими в широком диапазоне продуктов временной полосы. Два примера для TxB = 100 и 250 показаны ниже. Они имеют фазовый угол, близкий к значению π /4 в пределах диапазона чирпа. $\omega _{0}\pm \Delta \Omega /2$ и они начинают существенно меняться только для частот за пределами этого диапазона.

представляют квадратичный фазовый член Φ 1( ω ) и его функция групповой задержки ( = -d Φ 1/d( ω Следовательно, для частот в пределах диапазона развертки чирпа наибольший интерес ) ). Ниже показан график групповой задержки. И эта функция, и фаза Φ 1( ω ) не зависят от значения произведения ширины полосы времени. Как и ожидалось, групповая задержка представляет собой линейную функцию длительностью T секунд при развертке частоты Δ Ω рад.

Остаточный фазовый член добавляет лишь незначительные возмущения к этой характеристике в диапазоне частот. $\Delta \Omega \pm \Delta \Omega /2$. На частотах вне этого диапазона Φ 2( ω ) быстро отклоняется от π /4, и поэтому полная фаза там будет серьезно отклоняться от квадратичного закона. К счастью, энергетическая составляющая спектра чирпа на этих частотах очень мала (как будет показано в следующем разделе).

Нелинейные сигналы

Когда частотно-временная характеристика нелинейна, интеграл Фурье оценить трудно. В таких случаях можно прибегнуть к такому методу аппроксимации, как аппроксимация стационарной фазы , или использовать численные методы.

Методом стационарной фазы

Часто (как в радиолокационных приложениях) a(t) является медленно меняющейся функцией времени, а фаза θ (t) является колебательной и быстро меняется в диапазоне интегрирования. При таких формах сигналов для исследования спектра можно использовать приближение стационарной фазы. Метод основан на том факте, что основные вклады в интеграл Фурье вносятся из области, где скорость изменения фазы минимальна, т.е. когда

${\frac {d}{dt}}[(\omega _{0}-\omega )t+\theta (t)]=0\qquad or\qquad (\omega -\omega _{0})-\theta '(t)=0$

Если θ (t) не является постоянной величиной, момент времени t _s , в котором фаза является стационарной, будет меняться в зависимости от мгновенной частоты ω _s .
Выражая разницу между ( ω _s - ω ₀ ).t и θ (t) как ряд Тейлора относительно времени t _s , но отбрасывая все члены, кроме первых трех (из которых второй член здесь равен нулю), Фурье Интеграл можно записать приближенно как

$S(\omega )\approxeq a(t_{s})\int _{t_{s}-\delta }^{t_{s}+\delta }\exp \left[-j\left\{(\omega _{s}-\omega _{0})\cdot t-\theta (t_{s})-{\frac {\theta ''(t_{s})}{2}}\cdot (t-t_{s})^{2}\right\}\right]\cdot dt$

В этом уравнении t _s представляет собой постоянный момент времени, поэтому члены, зависящие только от t _s, могут быть вынесены за пределы интеграла. Выражение упрощается до
$S(\omega )\approxeq {\sqrt {2\pi }}\cdot {\frac {a(t_{s})}{\sqrt {|\theta ''(t)|}}}\cdot \exp \left[j\left\{(\omega _{0}-\omega _{s})t+\theta (t_{s})+{\frac {\pi }{4}}\right\}\right]$
так
$|S(\omega _{t})|^{2}\approxeq 2\pi \cdot {\frac {a^{2}(t)}{|\theta ''(t)|}}$

где ω _t используется для обозначения зависимости частотной переменной от t.
Это очень полезное выражение, связывающее профиль спектра с амплитудными и фазовыми характеристиками чирпа.

Для выполнения обратного процесса, т.е. для нахождения функции s(t) временной области с учетом данных частотной области, получают обратное преобразование Фурье.

$s(t)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }|S(\omega )|\cdot \exp[j(\Phi (\omega )+\omega \cdot t)]\cdot d\omega$

где Φ (x) — фазовая функция спектра. Точки стационарной фазы для этого подынтегрального выражения расположены в точках

$\Phi '(\omega )=-t$

а следствие, эквивалентное полученному для спектра, может быть получено методом стационарной фазы и равно

$a^{2}(t_{\omega })\approxeq {\frac {1}{2\pi }}\cdot {\frac {|S(\omega )|^{2}}{|\Phi ''(\omega )|}}$

Фактически, анализ стационарной фазы дает следующие (приблизительные) парные соотношения Фурье:
$a(t)\cdot \exp[j\theta (t)]\approxeq {\frac {1}{2\pi }}\cdot \int _{-\infty }^{\infty }S(\omega )|\cdot \exp[j\{\Phi (\omega )+\omega \cdot t\}]\cdot d\omega$
и
$|S(\omega )|\cdot \exp[j\Phi (\omega )]\approxeq \int _{-\infty }^{\infty }a(t)\cdot \exp[-j\{\omega t-\theta (t)\}]dt$

Следовательно, приближенные выражения для a(t) и θ спектр, включая его фазовую функцию Φ ( ω (t) могут быть получены, когда задан ), и, аналогично, приближенные выражения для |S( ω | и Φ ( ω ) могут быть получены получаются при задании характеристик сигнала. В литературе приведено несколько примеров процедуры.

Хотя эти соотношения являются лишь приблизительными, их точность повышается по мере увеличения произведения временной полосы пропускания. В тех случаях, когда огибающая сигнала и модуль спектра определяются плавно изменяющейся функцией Гаусса , тогда произведение T. Δ F, равное 15, даст приемлемые результаты, но если и a(t), и |S( ω )| определяются прямоугольными функциями, то произведение T. Δ F должно быть намного больше, обычно больше 100.

Примеры

Обычно в случае радара a(t) является постоянной величиной на протяжении всего сигнала и для удобства принимается здесь равным единице. Таким образом, фазовые и амплитудные характеристики в частотной области связаны соотношением

$\Phi ''(\omega )=\pm {\frac {1}{2\pi }}\cdot |S(\omega )|^{2}$

Существует два решения для Φ ( ω ), которые являются комплексно сопряженными друг другу. Два фильтра с этими характеристиками могут использоваться в качестве фильтров передатчика и приемника радиолокационной системы и являются взаимозаменяемыми.
Характеристика групповой задержки D( ω ), (где D( ω ) = -d Φ /d ω ), равна

$D(\omega )=-\Phi '(\omega )=-\int _{0}^{\infty }\Phi ''(\omega )\cdot d\omega +K$
так
$D(\omega )=\pm {\frac {1}{2\pi }}\cdot \int _{0}^{\infty }|S(\omega )|^{2}\cdot d\omega +K$

Таким образом, в случае прямоугольной временной огибающей дисперсионная характеристика задержки определяется интегралом от квадрата огибающей. Если взять положительный знак, то групповая задержка увеличивается с увеличением частоты и наоборот. Результат является лишь приблизительным, но он более точен для больших значений произведения временной полосы пропускания.
Рассмотрим в качестве примера случай спектра, однородного в диапазоне от - ω _max /2 до ω _max /2, тогда

$|S(\omega )|^{2}=A\qquad for\qquad |\omega |<{\frac {\omega _{max}}{2}}$
так
$D(\omega )={\frac {1}{2\pi }}\cdot \int A\cdot d\omega +K={\frac {A}{2\pi }}\cdot \omega +K$

Положим D(- ω _max /2) = 0 и D( ω _max /2) = T, где T — длительность импульса, тогда K = T/2 и A = (2 π T)/ ω _max.
итак, наконец
$D(\omega )=T\cdot \left[{\frac {1}{2}}+{\frac {\omega }{\omega _{max}}}\right]$

Как и ожидалось, частотный спектр с плоской вершиной соответствует линейной развертке частоты.

Линейный чирп — это лишь один частный случай, который в любом случае можно более точно рассчитать методами предыдущего раздела. Особая полезность метода стационарной фазы заключается в его способности давать результаты, когда развертка частоты является нелинейной. В таких случаях спектральную характеристику можно сформировать так, чтобы она соответствовала некоторым желаемым критериям проектирования, например, малым боковым лепесткам при сжатии ЛЧМ. Одно из таких семейств спектральных функций, которое было изучено дается

$|S(\omega )|^{2}=A_{n}\cdot cos^{n}\left({\frac {\pi \omega }{\omega _{max}}}\right)\qquad where\qquad |\omega |<{\frac {\omega _{max}}{2}}\qquad and\ n\ is\ an\ integer$

Аналогично тому, как это было сделано выше, можно найти характеристики групповой задержки этих функций, и были рассчитаны результаты для n = 1–4.
Хотя эти косинусные функции поддаются математическим манипуляциям, на практике их редко выбирают для определения спектральных характеристик ЛЧМ, поскольку при сжатии они дают широкие основные импульсы с высокими уровнями боковых лепестков. Лучшая характеристика (среди многих) - функция Хэмминга, определяемая формулой

$|S(\omega )|^{2}=A\cdot \left[0.54+0.46\cdot cos\left({\frac {2\pi \omega }{\omega _{max}}}\right)\right]=A\cdot \left[0.08+0.92\cdot cos^{2}\left({\frac {\pi \omega }{\omega _{max}}}\right)\right]$

Показан график этой характеристики, построенный в диапазоне от - ω _max /2 до ω _max /2.

Применяя приведенные выше уравнения, можно получить характеристику групповой задержки, которая достигает этой спектральной формы. Это

$D_{H}(\omega )=T\cdot \left[{\frac {1}{2}}+{\frac {\omega }{\omega _{max}}}+{\frac {1.7037}{4\pi }}\cdot sin\left({\frac {2\pi \omega }{\omega _{max}}}\right)\right]$

Теперь, поскольку принцип стационарной фазы показывает, что существует прямая связь между прошедшим временем и мгновенной задержкой сигнала, тогда для окна Хэмминга t/T может быть связано с ω / ω _max соотношением

${\frac {t}{T}}={\frac {1}{2}}+{\frac {\omega }{\omega _{max}}}+{\frac {1.7037}{4\pi }}\cdot sin\left({\frac {2\pi \omega }{\omega _{max}}}\right)$

Здесь показана характеристика времени как функции частоты. Инвертирование графика дает более обычный (и более полезный) график зависимости частоты от времени, который также показан.

Другие формы спектра можно исследовать таким же способом, и результаты, хотя и приблизительные, оказываются на удивление точными, особенно когда произведение временной ширины импульса велико.

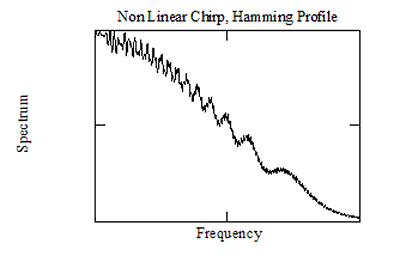
Метод стационарной фазы не предсказывает и не устраняет пульсации Френеля, поэтому он не может предложить никаких средств, с помощью которых эти пульсации можно было бы минимизировать. В качестве примера на рисунке ниже показан спектр чирпа с T. Δ F =250, полученный для нелинейного чирпа, стремящегося соответствовать окну Хэмминга, с использованием методов, описанных выше. На рисунке видно, что спектральный профиль довольно хорошо соответствует характеристике Хэмминга, однако весьма заметны ряби Френеля, не предсказанные методом.

С помощью численных методов

Выборка

Если интеграл Фурье не может быть вычислен аналитическими методами, приближенное решение обычно возможно с помощью численного анализа . функции Такая процедура требует выборки , обычно через равные промежутки времени.

Одним из последствий дискретизации является то, что результирующий спектр является периодическим в частотной области. В дополнение к (желаемому) спектру основной полосы существуют дополнительные версии спектра, сосредоточенные на кратных частоте дискретизации. Чтобы гарантировать отсутствие перекрытия частотных данных (т. е. отсутствия наложения ), Найквиста должна соблюдаться теорема выборки . На практике рекомендуется частота дискретизации существенно выше той, которая диктуется теоремой выборки.

Спектр дискретизированного сигнала — преобразование Фурье сигнала дискретного времени.

Самый простой способ аппроксимировать интеграл, например интеграл Фурье, — использовать стандартное « правило прямоугольника » для численного интегрирования. Этот метод предполагает, что значение сигнала, полученное в момент выборки, остается постоянным в течение одного интервала выборки, пока не будет взята следующая выборка. Эту процедуру иногда называют «генератором коробчатого вагона» или выборкой и удержанием нулевого порядка. Если временной интервал между выборками равен W, то s _n = s(nW), и искомый интеграл получается приближенно путем суммирования прямоугольных площадей.

Полученный таким образом результат представляет собой свертку прямоугольного импульса с размером шага W с импульсами, расположенными в моменты выборки, с весами, равными значениям выборки. В результате на интересующий спектр будет наложена частотная характеристика образца и удержано: а спектр дискретизированного сигнала Ss определяется выражением:

$Ss(\omega ))=W{\frac {\sin(\omega W/2)}{\omega W/2}}\cdot \left[\sum _{n=-\infty }^{\infty }s_{n}\cdot \exp(-jn\omega W)\right]$

Первая часть выражения, т.е. часть «sin(x)/x», представляет собой частотную характеристику выборки и удержания. Его амплитуда уменьшается с частотой и падает до 63% от своего пикового значения на половине частоты дискретизации и равна нулю на кратных этой частоте (поскольку f _s =1/W).

Второй член в уравнении называется преобразованием Фурье дискретного сигнала s _n . Это непрерывная функция по всем ω , требующая бесконечного числа суммирований. На практике процесс суммирования можно сократить до конечного числа выборок N, возможно, потому, что форма сигнала является периодической или равна нулю за пределами диапазона выборок. Более того, поскольку один и тот же спектр повторяется бесконечно, можно ограничить интерес спектральными данными в диапазоне от - ω _s /2 до + ω _s /2.

Например, экспоненциальный чирп (с его максимальной частотой значительно ниже предела Найквиста) дискретизируется в 256 точках, как показано.

Показан выборочный спектр Ss( ω ) этого сигнала, рассчитанный с использованием приведенного выше уравнения. Чтобы упростить график, были отображены только результаты при положительных частотах. На схеме хорошо видно влияние частотного спектра схемы удержания нулевого порядка.

Основная часть спектра показана более подробно на следующем рисунке, а отклик демонстрирует отчетливый наклон, значительно ниже на более высоких частотах.

Хотя характеристика удержания нулевого порядка оказывает небольшое влияние на этот результат, крутизна в основном обусловлена ​​свойствами чирпа. Форма сигнала сравнительно быстро распространяется по высоким частотам и тратит больше времени на сканирование низких частот, следовательно, на высоких частотах содержится меньше энергии, а на более низких - больше. (С другой стороны, линейный чирп имеет номинально плоский спектр, поскольку его частоты колеблются с одинаковой скоростью, как показано на некоторых предыдущих графиках).

С помощью дискретного преобразования Фурье

Если мы ограничим интерес к выходному спектру конечным числом дискретных точек данных (= N) на частотах ω _m , определяемых формулой
$\omega _{m}={\frac {2\pi m}{NW}}\qquad for\qquad m=0,1,2,...N-1$

тогда формула для расчета дискретного преобразования Фурье будет иметь вид

$Ss_{m}\quad =Ss\left(j{\frac {2\pi m}{NW}}\right)\quad =\quad \sum _{n=0}^{N-1}s_{n}\cdot exp(-j\left({\frac {2\pi mn}{N}}\right)$

Расчеты могут быть выполнены с помощью простого компьютерного алгоритма. но это не очень эффективно при использовании компьютера. Следовательно, были разработаны более эффективные алгоритмы, особенно быстрое преобразование Фурье (БПФ). Компьютерные программы, реализующие БПФ, широко доступны в литературе. и в собственных программах САПР, таких как Mathcad , MATLAB и Mathematica .
В следующем примере линейный чирп с произведением временной полосы пропускания, равным 25, дискретизируется в 128 точках (т. е. N = 128). На рисунке показаны образцы реальной части сигнала – обратите внимание, что это образцы во временной области. Процесс БПФ предполагает, что форма сигнала является циклической, поэтому эти 128 точек данных можно рассматривать как часть бесконечно повторяющейся последовательности во времени.

Linear chirp with TB=25 and N=128

Путем вычисления N-точечного БПФ этих данных получается дискретный спектр последовательности. Величина этого спектра показана на прилагаемом рисунке, где эти точки данных являются выборками по частоте. Данные цикличны, поэтому на графике точка нулевой частоты находится в точке n = 0, а также в точке n = 128 (т. е. обе точки имеют одинаковую частоту). Точка n = 64 соответствует +fs/2 (а также -fs/2).

Spectrum of Linear Chirp, TB=25, N=128

Для более детального отображения спектра (но не обязательно с большим разрешением) ), временная последовательность может быть расширена путем заполнения нулями. Например, расширение временной последовательности из 128 точек нулями для получения N = 4096 приводит к тому, что часть спектра, первоначально представленная в 16 выборках, теперь представлена ​​в 512 выборках, как показано.

Спектральный разброс

За пределами диапазона частот развертки ЛЧМ-импульса спектральная составляющая очень незначительна, и это особенно верно для сигналов, в которых произведение времени на полосу пропускания велико. Полная линия на графике соседнего рисунка показывает результаты для линейных чирпов. Он показывает, например, что только около 2% общей мощности приходится на частоты вне диапазона развертки Δ F, когда временная полоса пропускания равна 100, и менее 1/2%, когда T. Δ F равна 500.
В случае нелинейного чирпа или линейного чирпа, сформированного путем взвешивания по амплитуде, доля мощности вне Δ F еще ниже, как показано на графике, где пунктирная линия соответствует спектрам с профилями Хэмминга.
Этот низкий спектральный разброс особенно важен, когда модулирующие сигналы должны быть оцифрованы, поскольку он позволяет выбрать частоту дискретизации, которая лишь немного превышает двойное максимальное отклонение частоты ЛЧМ.

Уменьшение спектральной пульсации

Пульсации Френеля в спектре чирпа очень заметны, особенно когда продукты временной полосы малы (скажем, менее 50), и их присутствие приводит к высоким временным уровням боковых лепестков, когда чирпы подвергаются сжатию импульсов, как в радиолокационных и гидролокационных системах. Они возникают из-за внезапных разрывов формы сигнала в начале и в конце импульса.

Хотя существует ряд процедур, которые можно применить для снижения уровня пульсаций, не все они одинаково эффективны. Более того, некоторые из способов требуют формирования амплитуды или амплитудной модуляции ЛЧМ-импульса, и это делает эти способы непригодными, когда, например, ЛЧМ-импульсы должны передаваться усилителем мощности, работающим в условиях, близких к предельным. Для таких систем подходят только методы, использующие предыскажение частоты (или фазы).

Представляем времена подъема и спада конечной продолжительности

Если переходы в начале и конце чирпа сделать менее резкими (или более «округленными»), то достигается уменьшение амплитуды пульсаций. Длительность двух переходных областей должна составлять лишь небольшую часть длительности импульса, и предлагаемые значения находятся в диапазоне от 2/ Δ F до 3/ Δ F. но, как и ожидалось, когда произведение импульса на ширину полосы пропускания мало, необходимы более длительные переходные периоды. Фактические профили этих областей нарастания и спада импульса не кажутся критическими и могут обеспечиваться, например, фильтрами ограничения полосы в аналоговых реализациях и линейным наклоном в цифровых реализациях.

Два примера показывают спектры линейных чирпов с конечным временем нарастания. Первый предназначен для чирпа с временной полосой 250, где время нарастания и спада составляет 4% от общей длительности импульса, а второй — для чирпа с временной полосой 25, где время нарастания и спада составляет 10%. от общей суммы. Эти два спектра демонстрируют заметное снижение амплитуды пульсаций по сравнению со спектрами немодифицированных линейных чирпов, показанными ранее.

Применение фазового или частотного искажения к ЛЧМ-импульсу

Аналогичный метод можно применить к частотной характеристике ЛЧМ-сигнала путем добавления к частотной характеристике ЛЧМ-сигнала сегментов линейного ЧМ- искажения (квадратичное фазовое модуляционное искажение), как показано. Метод эффективен, поскольку амплитудные и фазовые искажения, имеющие функциональное сходство, могут давать аналогичные эффекты, когда коэффициенты искажений малы.

Это добавленное искажение называется «предыскажением». Первоначально для достижения хороших результатов были определены предлагаемые значения для этих областей искажений:
$\Delta f_{p}=0.75\Delta F\qquad and\qquad \delta =1/\Delta F$

В 1988 году более поздняя работа предложили немного другие значения, а именно:
$\Delta f_{p}=0.73\Delta F\qquad and\qquad \delta =0.86/\Delta F$

Результаты можно дополнительно улучшить за счет оптимизации значений для каждой конкретной ситуации.

Ниже приведены два графика, показывающие влияние предварительной коррекции частоты для временной полосы 25 и 250. Их можно сравнить с результатами в предыдущих разделах.

Уменьшение пульсаций, достигаемое с помощью предварительной коррекции частоты, хотя и является значительным, считается менее успешным, чем то, которое достигается с помощью методов амплитудной модуляции, описанных в предыдущем разделе. Однако было предложено что, реализуя предварительную коррекцию кубической (а не квадратичной) фазы, можно достичь сопоставимых результатов.

Получение формы сигнала из целевого частотного спектра

В этом методе используется обратное преобразование Фурье для получения сигнала, спектр которого имеет фазовую характеристику выбранного чирпа, но новый профиль амплитуды, который является прямоугольным и свободным от пульсаций. Метод очень эффективен, но, к сожалению, полученная таким образом волна имеет полубесконечную продолжительность времени. Если для удобства вновь полученный сигнал усекается до практической длины, то в спектр снова вводится некоторая пульсация.

В качестве примера показан линейный импульсный сигнал с временной полосой пропускания 25 вместе с величиной его спектра (показанной сплошной линией), который, как было показано ранее, имеет большую пульсирующую составляющую. С помощью обратного БПФ можно найти ЛЧМ-сигнал, который в частотной области имеет ту же фазовую характеристику, что и раньше, но с прямоугольной амплитудной характеристикой, показанной пунктирной линией на графике. Форма сигнала с чирпом, возникающая в результате этого процесса, имеет очень большую продолжительность по времени, но когда она усекается, скажем, до длины 2T, то спектр снова приобретает некоторую пульсацию, как показано.

Применение оконных функций

Существует множество приложений, в которых спектр с прямоугольным профилем магнитуды не является идеальным. Например, когда сигнал с ЛЧМ сжимается с помощью согласованного фильтра, результирующий сигнал приближается к функции sinc и, следовательно, имеет раздражающе высокие боковые лепестки. Часто для улучшения характеристик импульса и снижения уровня боковых лепестков его спектр модифицируют, обычно до колоколообразного профиля. Аналогичные проблемы возникают при цифровой обработке сигналов , где формирование спектра обеспечивается оконной функцией — процесс, который иногда называют аподизацией . В случае антенной решетки аналогичное профилирование с помощью «весовых функций» используется для уменьшения пространственных боковых лепестков диаграммы направленности.

Хотя формирование спектра ЛЧМ можно применять в частотной области, лучшие результаты получаются, если формирование осуществляется во временной области. Примеры этого процесса показаны для линейных чирпов с произведениями временной полосы 250 и 25. Они были сформированы с помощью трехчленного окна Блэкмана-Харриса. данный
$|U(\omega )|^{2}=0.42323-0.49755\cos \left({\frac {2\pi \omega }{\omega _{max}}}\right)+0.07922\cos \left({\frac {4\pi \omega }{\omega _{max}}}\right)$
Видно, что спектры, теперь имеющие колоколообразную форму, лишены ряби.

Можно разработать нелинейные чирпы, которые имеют колоколообразный спектр, например окно Блэкмана-Харриса, которое только что обсуждалось, и, следовательно, будут демонстрировать меньшую пульсацию по сравнению с линейным чирпом. С помощью описанного ранее метода стационарной фазы можно получить приблизительную зависимость между временем и частотой:

${\frac {t}{T}}={\frac {1}{2}}+{\frac {\omega }{\omega _{max}}}+0.1871\sin \left({\frac {2\pi \omega }{\omega _{max}}}\right)+0.014895\sin \left({\frac {4\pi \omega }{\omega _{max}}}\right)$
Переставив уравнение, можно построить график зависимости частоты от времени, который выглядит примерно так, как показано справа.

Нелинейные чирпы со спектральными профилями окна Блэкмана-Харриса демонстрируют уменьшение пульсаций, но могут иметь разочаровывающие характеристики из-за профилей амплитуды с быстрым временем нарастания и спада.

В качестве примера ниже приведены два графика спектральных величин таких чирпов с произведением временной полосы пропускания 250 и 25 соответственно. Эти чирпы имеют пониженное содержание энергии во внешних частотных диапазонах, но все равно демонстрируют не идеальные характеристики.

См. также

• Сжатие импульсов — процесс, в котором используются сигналы с частотным или фазовым кодированием для улучшения отношения сигнала к шуму принимаемых сигналов.
• Сжатие чирпа — процесс сжатия только для чирпов.