Угловой диаметр

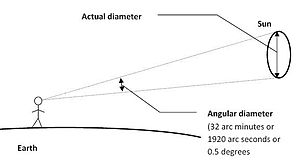
Угловой диаметр , угловой размер , видимый диаметр или видимый размер — это угловое расстояние, описывающее, насколько большой кажется сфера или круг с данной точки зрения. В науках о зрении его называют углом зрения , а в оптике — угловой апертурой (линзы ) . Угловой диаметр также можно рассматривать как угловое смещение , на которое глаз или камера должны повернуться, чтобы посмотреть с одной стороны видимого круга на противоположную сторону. Люди могут определить невооруженным глазом диаметры примерно до 1 угловой минуты (приблизительно 0,017° или 0,0003 радиан). ^[1] Это соответствует 0,3 м на расстоянии 1 км или восприятию Венеры как диска в оптимальных условиях.

Формула [ править ]

Угловой диаметр окружности , плоскость которой перпендикулярна вектору смещения между точкой зрения и центром указанной окружности, можно рассчитать по формуле ^[2]^[3]

\delta =2\arctan \left({\frac {d}{2D}}\right),

в котором $\delta$ угловой диаметр в градусах , $d$ - фактический диаметр объекта, а $D$ это расстояние до объекта. Когда $D\gg d$ , у нас есть $\delta \approx d/D$ , ^[4] и полученный результат выражен в радианах .

Для сферического объекта, действительный диаметр которого равен $d_{\mathrm {act} },$ и где $D$ — расстояние до центра сферы, угловой диаметр можно найти по следующей модифицированной формуле ^{[ нужна ссылка ]}

\delta =2\arcsin \left({\frac {d_{\mathrm {act} }}{2D}}\right)

Разница связана с тем, что видимые края сферы являются точками ее касания, которые находятся ближе к наблюдателю, чем центр сферы, и имеют расстояние между ними, меньшее фактического диаметра. Приведенную выше формулу можно найти, если понять, что в случае сферического объекта можно построить прямоугольный треугольник так, что его три вершины являются наблюдателем, центром сферы и одной из точек касания сферы, причем $D$ как гипотенуза и ${\frac {d_{\mathrm {act} }}{2D}}$ как синус. ^{[ нужна ссылка ]}

Разница существенна только для сферических объектов большого углового диаметра, поскольку значений для малых $x$ : ^[5]

\arcsin x\approx \arctan x\approx x.

Оценка углового диаметра с помощью руки [ править ]

Оценку углового диаметра можно получить, держа руку под прямым углом к полностью выпрямленной руке , как показано на рисунке. ^[6]^[7]^[8]

Использование в астрономии [ править ]

В астрономии размеры небесных объектов часто выражаются в терминах их углового диаметра, видимого с Земли , а не их фактических размеров. Поскольку эти угловые диаметры обычно невелики, их принято представлять в угловых секундах (″). Угловая секунда равна 1/3600 одного градуса (1°), а радиан — 180/ π градусов. Таким образом, один радиан равен 3600 × 180/. $\pi$ угловых секунд, что составляет около 206 265 угловых секунд (1 рад ≈ 206 264,806247 дюймов). Следовательно, угловой диаметр объекта с физическим диаметром d на расстоянии D , выраженный в угловых секундах, определяется выражением: ^[9]

\delta =206,265~(d/D)~\mathrm {arcseconds}

.

Эти объекты имеют угловой диаметр 1 дюйм:

предмет диаметром 1 см на расстоянии 2,06 км
объект диаметром 725,27 км на расстоянии 1 астрономической единицы (а.е.)
объект диаметром 45 866 916 км на расстоянии 1 светового года
объект диаметром 1 а.е. (149 597 871 км) на расстоянии 1 парсек (пк)

Таким образом, угловой диаметр орбиты Земли вокруг Солнца , если смотреть с расстояния 1 пк, равен 2 дюйма, поскольку 1 а.е. — средний радиус орбиты Земли.

Угловой диаметр Солнца на расстоянии одного светового года составляет 0,03 дюйма, а Земли — 0,0003 дюйма. Приведенный выше угловой диаметр Солнца 0,03 дюйма примерно такой же, как у человеческого тела на расстоянии диаметра Земли.

В этой таблице показаны угловые размеры примечательных небесных тел , видимых с Земли:

Небесный объект	Угловой диаметр или размер	Относительный размер
Магелланов поток	более 100°
Туманность Гум	36°
Млечный Путь	30° (на 360°)
Ширина вытянутой руки с вытянутой рукой	20°	353 метра на дистанции 1 км
Разлом Змеи-Орла	20° на 10°
Избыточная плотность большого пса	12° на 12°
Облако Смита	11°
Большое Магелланово Облако	10,75° на 9,17°	Примечание: самая яркая галактика , кроме Млечного Пути на ночном небе (0,9 видимой звездной величины (V))
петля Барнарда	10°
Туманность Зета Змееносца Sh2-27	10°
Ширина кулака с вытянутой вперед рукой	10°	175 метров на дистанции 1 км
Карликовая сфероидальная галактика Стрельца	7,5° на 3,6°
Туманность Северный Угольный Мешок	7° на 5° ^[10]
Туманность Угольный Мешок	7° на 5°
Лебедь OB7	4° на 7° ^[11]
Облачный комплекс Ро Змееносца	4,5° на 6,5°
Гиады	5°30 ′	Примечание: самое яркое звездное скопление на ночном небе, видимая звездная величина 0,5 (В).
Маленькое Магелланово Облако	5°20 ′ на 3°5 ′
Галактика Андромеды	3°10 ′ на 1°	Примерно в шесть раз больше Солнца или Луны. видно только гораздо меньшее ядро Без фотографии с длинной выдержкой .
Харон (с поверхности Плутона)	3°9’
Туманность Вуаль	3°
Туманность Сердце	2,5° на 2,5°
Вестерхаут 5	2,3° на 1,25°
Ш2-54	2.3°
Туманность Киля	2° на 2°	Примечание: самая яркая туманность на ночном небе, видимая звездная величина 1,0 (В).
Туманность Северная Америка	2° на 100 ′
Земля на небе Луны	2° - 1°48 ′ ^[12]	На земном небе выглядит примерно в три-четыре раза больше Луны.
Туманность Ориона	1°5 ′ на 1°
Ширина мизинца в вытянутой руке	1°	17,5 метра на дистанции 1 км
Ио (вид с «поверхности» Юпитера)	35’ 35”
Луна	34 ′ 6″ – 29 ′ 20″	В 32,5–28 раз больше максимального значения Венеры (оранжевая полоса внизу) / 2046–1760 дюймов. Луна имеет диаметр 3474 км.
Солнце	32 ′ 32″ – 31 ′ 27″	В 31–30 раз больше максимального значения Венеры (оранжевая полоса внизу) / 1952–1887 гг. Диаметр Солнца составляет 1 391 400 км.
Тритон (С «поверхности» Нептуна)	28’ 11”
Угловой размер расстояния между Землей и Луной, если смотреть с Марса , в нижнем соединении	около 25 '
Ариэль (С «поверхности» Урана)	24’ 11”
Ганимед (С «поверхности» Юпитера)	18’ 6”
Европа (С «поверхности» Юпитера)	17’ 51”
Умбриэль ((С «поверхности» Урана)	16’ 42”
Туманность Хеликс	примерно 16 ′ на 28 ′
Шпиль в туманности Орла	4 ′ 40″	длина 280″
Венера	1 ′ 6″ – 0 ′ 9.7″
Международная космическая станция (МКС)	1 ′ 3″	^[13] МКС имеет ширину около 108 м.
Минимальный диаметр, различимый человеческим глазом	1 ′	^[14] 0,3 метра на расстоянии 1 км ^[15] Для видимости объектов с меньшими видимыми размерами смотрите необходимые видимые величины .
Около 100 км по поверхности Луны	1 ′	Сопоставимо с размером таких объектов, как большие лунные кратеры, такие как кратер Коперник , заметное яркое пятно в восточной части Oceanus Procellarum на убывающей стороне, или кратер Тихо в яркой области на юге ближней стороны Луны. .
Юпитер	50.1″ – 29.8″
Минимально разрешаемый разрыв между двумя линиями для человеческого глаза	40″	зазор 0,026 мм, если смотреть с расстояния 15 см ^[14]^[15]
Марс	25.1″ – 3.5″
Видимый размер Солнца, вид из 90377 Седны в афелии.	20,4 дюйма
Сатурн	20.1″ – 14.5″
Меркурий	13.0″ – 4.5″
Уран	4.1″ – 3.3″
Нептун	2.4″ – 2.2″
Ганимед	1.8″ – 1.2″	Ганимед имеет диаметр 5268 км.
Космонавт ( ~1,7 м) на расстоянии 350 км, средняя высота МКС.	1″
Минимальный разрешаемый диаметр Галилео Галилея крупнейших 38-мм телескопов-рефракторов	~1″	^[16] Примечание: 30x ^[17] увеличение, сравнимое с очень сильными современными наземными биноклями
Церера	0.84″ – 0.33″
Веста	0.64″ – 0.20″
Плутон	0.11″ – 0.06″
Эрис	0.089″ – 0.034″
Р Дорадус	0.062″ – 0.052″	Примечание: R Дорадус считается внесолнечной звездой с самым большим видимым размером, если смотреть с Земли.
Бетельгейзе	0.060″ – 0.049″
Альфард	0.00909″
Ро Кассиопеи	0.0072″
Альфа Центавра А	0.007″
Канопус	0.006″
Сириус	0.005936″
Альтаир	0.003″
Денеб	0.002″
Рядом с Центавром	0.001″
Альнитак	0.0005″
Проксима Центавра б	0.00008″
Горизонт событий черной дыры M87* в центре галактики M87, снимок телескопа Event Horizon в 2019 году.	0.000025″ ( 2.5 × 10 ⁻⁵)	Сравнимо с теннисным мячом на Луне.
Звезда, подобная Альнитак , на расстоянии, где космический телескоп Хаббл. ее мог бы увидеть ^[18]	6 × 10 ⁻¹⁰ угловая секунда

На этой фотографии сравниваются видимые размеры Юпитера и его четырех галилеевых спутников ( Каллисто в максимальной элонгации ) с видимым диаметром полной Луны во время их соединения 10 апреля 2017 года.

Угловой диаметр Солнца, если смотреть с Земли, примерно в 250 000 раз больше диаметра Сириуса . (Сириус имеет в два раза больший диаметр и расстояние до него в 500 000 раз больше; Солнце находится в 10 ¹⁰ раз ярче, что соответствует соотношению угловых диаметров 10 ⁵, поэтому Сириус примерно в 6 раз ярче на единицу телесного угла .)

Угловой диаметр Солнца также примерно в 250 000 раз больше, чем у Альфы Центавра А (у него примерно такой же диаметр, а расстояние в 250 000 раз больше; размер Солнца 4×10 ¹⁰ раз ярче, что соответствует соотношению угловых диаметров 200 000, поэтому Альфа Центавра A немного ярче на единицу телесного угла).

Угловой диаметр Солнца примерно такой же, как и у Луны . (Диаметр Солнца в 400 раз больше, как и расстояние до него; Солнце в 200 000–500 000 раз ярче полной Луны (цифры различаются), что соответствует соотношению угловых диаметров 450 к 700, поэтому небесное тело с диаметром 2,5–4 дюйма, а та же яркость на единицу телесного угла будет иметь ту же яркость, что и полная Луна.)

Хотя Плутон физически больше Цереры, при наблюдении с Земли (например, через космический телескоп Хаббл ) Церера имеет гораздо больший видимый размер.

Угловые размеры, измеряемые в градусах, полезны для больших участков неба. (Например, три звезды Пояса охватывают около 4,5° углового размера.) Однако для измерения угловых размеров галактик, туманностей и других объектов ночного неба необходимы гораздо более точные единицы .

Таким образом, степени подразделяются следующим образом:

360 градусов (°) по полному кругу
60 угловых минут ( ′ ) в одном градусе
60 угловых секунд (″) в одной угловой минуте

Для сравнения: полная Луна, если смотреть с Земли, составляет около 1 ⁄ 2 °, или 30 ′ (или 1800″). Движение Луны по небу можно измерить по угловому размеру: примерно 15° в час или 15 дюймов в секунду. Линия длиной в одну милю, нарисованная на поверхности Луны, с Земли может показаться, что ее длина составляет около 1 дюйма.

Минимальное, среднее и максимальное расстояния Луны от Земли с ее угловым диаметром, если смотреть с поверхности Земли, в масштабе

В астрономии обычно трудно напрямую измерить расстояние до объекта, однако объект может иметь известный физический размер (возможно, он похож на более близкий объект с известным расстоянием) и измеримый угловой диаметр. В этом случае формулу углового диаметра можно инвертировать, чтобы получить расстояние по угловому диаметру до удаленных объектов как

d\equiv 2D\tan \left({\frac {\delta }{2}}\right).

В неевклидовом пространстве, таком как наша расширяющаяся Вселенная, расстояние по угловому диаметру является лишь одним из нескольких определений расстояния, поэтому до одного и того же объекта могут быть разные «расстояния». См. Меры расстояний (космология) .

Некруглые объекты [ править ]

Многие объекты глубокого космоса, такие как галактики и туманности, кажутся некруглыми, и поэтому обычно им присваиваются две меры диаметра: большая ось и малая ось. Например, Малое Магелланово Облако имеет видимый диаметр 5°20’ × 3°5’.

Дефект освещения [ править ]

Дефект освещенности — это максимальная угловая ширина неосвещенной части небесного тела, видимой данным наблюдателем. Например, если объект имеет дугу 40 дюймов в поперечнике и освещен на 75%, дефект освещенности составит 10 дюймов.

См. также [ править ]

Ссылки [ править ]

^ Янофф, Мирон; Дукер, Джей С. (2009). Офтальмология, 3-е издание . МОСБИ Эльзевир. п. 54. ИСБН 978-0444511416 .
^ Это можно получить, используя формулу длины хорды, найденную в «Круговой сегмент» . Архивировано из оригинала 21 декабря 2014 г. Проверено 23 января 2015 г.
^ «Угловой диаметр | Хранилище формул Wolfram» . resources.wolframcloud.com . Проверено 10 апреля 2024 г.
^ «Примечания 7A: угловой размер/расстояние и площади» (PDF) .
^ «Ряд Тейлора для функции Арктана» (PDF) . Архивировано из оригинала (PDF) 18 февраля 2015 г. Проверено 23 января 2015 г.
^ «Системы координат» . Архивировано из оригинала 21 января 2015 г. Проверено 21 января 2015 г.
^ «Фотосъемка спутников» . 8 июня 2013 г. Архивировано из оригинала 21 января 2015 г.
^ Викиверситет: Лаборатории физики и астрономии/Угловой размер
^ Майкл А. Сидс; Дана Э. Бэкман (2010). Звезды и галактики (7-е изд.). Брукс Коул. п. 39. ИСБН 978-0-538-73317-5 .
^ О'Мира, Стивен Джеймс (6 августа 2019 г.). «Мешки с углем Лебедя» . Астрономия.com . Проверено 10 февраля 2023 г.
^ Добаси, Кадзухито; Мацумото, Томоаки; Симойкура, Томоми; Сайто, Хиро; Акисато, Ко; Охаси, Кенджиро; Накагоми, Кейсуке (24 ноября 2014 г.). «Сталкивающиеся нити и массивное плотное ядро в молекулярном облаке Cygnus Ob 7». Астрофизический журнал . 797 (1). Американское астрономическое общество: 58. arXiv : 1411.0942 . Бибкод : 2014ApJ...797...58D . дои : 10.1088/0004-637x/797/1/58 . ISSN 1538-4357 . S2CID 118369651 .
^ Горкавый, Ник; Кротков, Николай; Маршак, Александр (24 марта 2023 г.). «Наблюдения Земли с поверхности Луны: зависимость от лунной либрации» . Методы измерения атмосферы . 16 (6). Коперник ГмбХ: 1527–1537. Бибкод : 2023AMT....16.1527G . дои : 10.5194/amt-16-1527-2023 . ISSN 1867-8548 .
^ «Задача 346: Международная космическая станция и солнечное пятно: исследование угловых масштабов» (PDF) . Космическая математика @ НАСА! . 19 августа 2018 г. Проверено 20 мая 2022 г.
^ Перейти обратно: ^а ^б Вонг, Ян (24 января 2016 г.). «Насколько маленькие могут быть видны невооруженным глазом?» . Журнал BBC Science Focus . Проверено 23 мая 2022 г.
^ Перейти обратно: ^а ^б «Острые глаза: насколько хорошо мы действительно видим?» . Наука в школе – scienceinschool.org . 07.09.2016 . Проверено 23 мая 2022 г.
^ Грейни, Кристофер М. (10 декабря 2006 г.). «Точность наблюдений Галилея и ранние поиски звездного параллакса». arXiv : физика/0612086 . дои : 10.1007/3-540-50906-2_2 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
^ «Телескоп Галилея – Как он работает» . Онлайн-выставки — Институт и Музей истории науки (на итальянском языке) . Проверено 21 мая 2022 г.
^ Угловой диаметр в 800 000 раз меньше, чем у Альнитака, если смотреть с Земли. Альнитак — голубая звезда, поэтому для своего размера она излучает много света. Если бы она была в 800 000 раз дальше, то ее звездная величина была бы 31,5, что соответствует пределу того, что может видеть Хаббл.

Внешние ссылки [ править ]

Формула малого угла (архивировано 7 октября 1997 г.)
Наглядное пособие для определения видимого размера планет

[Yanoff2009-1] Янофф, Мирон; Дукер, Джей С. (2009). Офтальмология, 3-е издание . МОСБИ Эльзевир. п. 54. ИСБН 978-0444511416 .

[2] Это можно получить, используя формулу длины хорды, найденную в «Круговой сегмент» . Архивировано из оригинала 21 декабря 2014 г. Проверено 23 января 2015 г.

[3] «Угловой диаметр | Хранилище формул Wolfram» . resources.wolframcloud.com . Проверено 10 апреля 2024 г.

[4] «Примечания 7A: угловой размер/расстояние и площади» (PDF) .

[5] «Ряд Тейлора для функции Арктана» (PDF) . Архивировано из оригинала (PDF) 18 февраля 2015 г. Проверено 23 января 2015 г.

[6] «Системы координат» . Архивировано из оригинала 21 января 2015 г. Проверено 21 января 2015 г.

[7] «Фотосъемка спутников» . 8 июня 2013 г. Архивировано из оригинала 21 января 2015 г.

[8] Викиверситет: Лаборатории физики и астрономии/Угловой размер

[9] Майкл А. Сидс; Дана Э. Бэкман (2010). Звезды и галактики (7-е изд.). Брукс Коул. п. 39. ИСБН 978-0-538-73317-5 .

[OMeara_2019-10] О'Мира, Стивен Джеймс (6 августа 2019 г.). «Мешки с углем Лебедя» . Астрономия.com . Проверено 10 февраля 2023 г.

[Dobashi_Matsumoto_Shimoikura_Saito_2014_p=58-11] Добаси, Кадзухито; Мацумото, Томоаки; Симойкура, Томоми; Сайто, Хиро; Акисато, Ко; Охаси, Кенджиро; Накагоми, Кейсуке (24 ноября 2014 г.). «Сталкивающиеся нити и массивное плотное ядро в молекулярном облаке Cygnus Ob 7». Астрофизический журнал . 797 (1). Американское астрономическое общество: 58. arXiv : 1411.0942 . Бибкод : 2014ApJ...797...58D . дои : 10.1088/0004-637x/797/1/58 . ISSN 1538-4357 . S2CID 118369651 .

[Gorkavyi_Krotkov_Marshak_2023_pp._1527–1537-12] Горкавый, Ник; Кротков, Николай; Маршак, Александр (24 марта 2023 г.). «Наблюдения Земли с поверхности Луны: зависимость от лунной либрации» . Методы измерения атмосферы . 16 (6). Коперник ГмбХ: 1527–1537. Бибкод : 2023AMT....16.1527G . дои : 10.5194/amt-16-1527-2023 . ISSN 1867-8548 .

[Angular_size-13] «Задача 346: Международная космическая станция и солнечное пятно: исследование угловых масштабов» (PDF) . Космическая математика @ НАСА! . 19 августа 2018 г. Проверено 20 мая 2022 г.

[Wong_2016-14] Перейти обратно: ^а ^б Вонг, Ян (24 января 2016 г.). «Насколько маленькие могут быть видны невооруженным глазом?» . Журнал BBC Science Focus . Проверено 23 мая 2022 г.

[Science_in_School_–_scienceinschool.org_2016-15] Перейти обратно: ^а ^б «Острые глаза: насколько хорошо мы действительно видим?» . Наука в школе – scienceinschool.org . 07.09.2016 . Проверено 23 мая 2022 г.

[Graney_2006-16] Грейни, Кристофер М. (10 декабря 2006 г.). «Точность наблюдений Галилея и ранние поиски звездного параллакса». arXiv : физика/0612086 . дои : 10.1007/3-540-50906-2_2 . {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )

[Esposizioni_on-line_-_Istituto_e_Museo_di_Storia_della_Scienza-17] «Телескоп Галилея – Как он работает» . Онлайн-выставки — Институт и Музей истории науки (на итальянском языке) . Проверено 21 мая 2022 г.

[18] Угловой диаметр в 800 000 раз меньше, чем у Альнитака, если смотреть с Земли. Альнитак — голубая звезда, поэтому для своего размера она излучает много света. Если бы она была в 800 000 раз дальше, то ее звездная величина была бы 31,5, что соответствует пределу того, что может видеть Хаббл.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]