Угловое расстояние

Угловое расстояние или угловое разделение — это мера угла между ориентацией двух прямых линий , лучей или векторов в трехмерном пространстве или центральный угол, образованный радиусами, проходящими через две точки на сфере . Когда лучи представляют собой линии видимости от наблюдателя на две точки в пространстве, это называется кажущимся расстоянием или кажущимся разделением .

Угловое расстояние появляется в математике (в частности, в геометрии и тригонометрии ) и во всех естественных науках (например, в кинематике , астрономии и геофизике ). В классической механике вращающихся объектов оно появляется наряду с угловой скоростью , угловым ускорением , угловым моментом , моментом инерции и крутящим моментом .

Используйте

Термин угловое расстояние (или расстояние ) технически является синонимом самого угла , но подразумевает линейное расстояние между объектами (например, парой звезд, наблюдаемых с Земли ).

Измерение

Поскольку угловое расстояние (или расстояние) концептуально идентично углу, оно измеряется в тех же единицах , например, в градусах или радианах , с использованием таких инструментов, как гониометры или оптические инструменты, специально разработанные для указания четко определенных направлений и записи соответствующих значений. углы (например, телескопы ).

Формулировка

Угловое разделение $\theta$ между точками A и B, если смотреть со стороны O

Для вывода уравнения, описывающего угловое расстояние между двумя точками, расположенными на поверхности сферы, если смотреть из центра сферы, воспользуемся примером двух астрономических объектов. $A$ и $B$ наблюдался с Земли. Объекты $A$ и $B$ определяются их небесными координатами , а именно их прямым восхождением (RA) , $(\alpha _{A},\alpha _{B})\in [0,2\pi ]$; и склонения (декабрь) , $(\delta _{A},\delta _{B})\in [-\pi /2,\pi /2]$. Позволять $O$ обозначают наблюдателя на Земле, предположительно находящегося в центре небесной сферы . Скалярное произведение векторов $\mathbf {OA}$ и $\mathbf {OB}$ равно:

$\mathbf {OA} \cdot \mathbf {OB} =R^{2}\cos \theta$

что эквивалентно:

$\mathbf {n_{A}} \cdot \mathbf {n_{B}} =\cos \theta$

В $(x,y,z)$ в кадре два унитарных вектора разлагаются на:

$$\mathbf {n_{A}} ={\begin{pmatrix}\cos \delta _{A}\cos \alpha _{A}\\\cos \delta _{A}\sin \alpha _{A}\\\sin \delta _{A}\end{pmatrix}}\mathrm {\qquad and\qquad } \mathbf {n_{B}} ={\begin{pmatrix}\cos \delta _{B}\cos \alpha _{B}\\\cos \delta _{B}\sin \alpha _{B}\\\sin \delta _{B}\end{pmatrix}}.$$

Поэтому,

$$\mathbf {n_{A}} \cdot \mathbf {n_{B}} =\cos \delta _{A}\cos \alpha _{A}\cos \delta _{B}\cos \alpha _{B}+\cos \delta _{A}\sin \alpha _{A}\cos \delta _{B}\sin \alpha _{B}+\sin \delta _{A}\sin \delta _{B}\equiv \cos \theta$$

затем:

$\theta =\cos ^{-1}\left[\sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\cos(\alpha _{A}-\alpha _{B})\right]$

малого

Вышеприведенное выражение справедливо для любого положения A и B на сфере. В астрономии часто бывает, что рассматриваемые объекты находятся на небе действительно близко: звезды в поле зрения телескопа, двойные звезды, спутники планет-гигантов Солнечной системы и т. д. В случае, когда $\theta \ll 1$ радиан, подразумевая $\alpha _{A}-\alpha _{B}\ll 1$ и $\delta _{A}-\delta _{B}\ll 1$, мы можем развить приведенное выше выражение и упростить его. В малоугловом приближении второго порядка приведенное выше выражение принимает вид:

$\cos \theta \approx 1-{\frac {\theta ^{2}}{2}}\approx \sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\left[1-{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}\right]$

значение

$1-{\frac {\theta ^{2}}{2}}\approx \cos(\delta _{A}-\delta _{B})-\cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}$

следовательно

$1-{\frac {\theta ^{2}}{2}}\approx 1-{\frac {(\delta _{A}-\delta _{B})^{2}}{2}}-\cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}$.

При условии $\delta _{A}-\delta _{B}\ll 1$ и $\alpha _{A}-\alpha _{B}\ll 1$, при развитии второго порядка оказывается, что $\cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}\approx \cos ^{2}\delta _{A}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{2}}$, так что

$\theta \approx {\sqrt {\left[(\alpha _{A}-\alpha _{B})\cos \delta _{A}\right]^{2}+(\delta _{A}-\delta _{B})^{2}}}$

Малое угловое расстояние

Плоская аппроксимация углового расстояния на небе

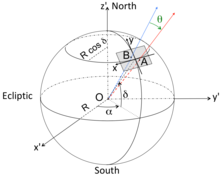
Если мы рассмотрим детектор, отображающий небольшое поле неба (размером намного меньше одного радиана) с $y$-ось направлена ​​вверх и параллельна меридиану прямого восхождения. $\alpha$и $x$- ось вдоль параллели склонения $\delta$, угловое разделение можно записать как:

$\theta \approx {\sqrt {\delta x^{2}+\delta y^{2}}}$

где $\delta x=(\alpha _{A}-\alpha _{B})\cos \delta _{A}$ и $\delta y=\delta _{A}-\delta _{B}$.

Обратите внимание, что $y$-ось равна склонению, тогда как $x$-ось — это прямое восхождение, модулированное $\cos \delta _{A}$ потому что сечение сферы радиуса $R$ по склонению (широте) $\delta$ является $R'=R\cos \delta _{A}$ (см. рисунок).

См. также

• миллирадиан
• Градиан
• Часовой угол
• Центральный угол
• Угол поворота
• Угловой диаметр
• Угловое смещение
• Расстояние большого круга
• Косинусное подобие § Угловое расстояние и подобие

Ссылки

• КАСТОР, автор Майкл А. Эрл. « Сферическая тригонометрия против векторного анализа» .
• Вайсштейн, Эрик В. «Угловое расстояние» . Математический мир .