Раковина (математика)

Раковина Никомеда, нарисованная с помощью аппарата, изображенного в комментариях Евтоция к трудам Архимеда.

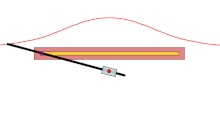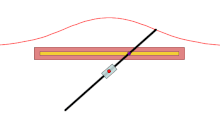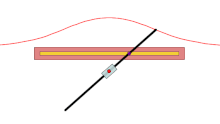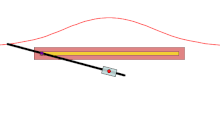
В геометрии раковина кривая — это , полученная из фиксированной точки $O$ , другой кривой и длины $d$ . Его изобрел древнегреческий математик Никомед . ^[1]

Описание

Для каждой линии, проходящей через $О$ , которая пересекает данную кривую в точке $А,$ две точки на линии, которые являются $d$ от $А,$ находятся на раковистой кости. Раковина, следовательно, является циссоидой данной кривой и кругом радиуса $d$ и центра $O$ . Их называют ракушками, потому что форма их внешних ветвей напоминает раковину .

В самом простом выражении используются полярные координаты с $О$ в начале координат. Если

r=\alpha (\theta )

выражает данную кривую, то

r=\alpha (\theta )\pm d

выражает раковину.

Если кривая — линия , то раковина — это раковина Никомеда .

Например, если кривая представляет собой линию $x = a$ , то полярная форма линии равна $r = a sec θ$ , и, следовательно, раковину можно выразить параметрически как

x=a\pm d\cos \theta ,\,y=a\tan \theta \pm d\sin \theta .

Лимасон — это раковина с кругом в качестве заданной кривой.

Так называемая ракушка де Слюза и ракушка Дюрера на самом деле не являются раковинами. Первый представляет собой строгую циссоиду, а второй — еще более общую конструкцию.