Экваториальная система координат

Экваториальная система координат — это небесная система координат, широко используемая для определения положения небесных объектов . Он может быть реализован в сферических или прямоугольных координатах, которые определяются началом координат в центре Земли , фундаментальной плоскостью, состоящей из проекции Земли экватора на небесную сферу (образующую небесный экватор ), основным направлением к мартовскому равноденствию , и соглашение для правшей . ^[1]^[2]

Начало координат находится в центре Земли, что означает, что координаты геоцентрические , то есть они видны из центра Земли, как если бы он был прозрачным . ^[3] Фундаментальная плоскость и основное направление означают, что система координат, хотя и совмещена с экватором и полюсом Земли , не вращается вместе с Землей, а остается относительно неподвижной по отношению к фоновым звездам . Правостороннее соглашение означает, что координаты увеличиваются к северу от фундаментальной плоскости и к востоку от нее.

Основное направление

Такое описание ориентации системы отсчета несколько упрощено; ориентация не совсем фиксирована. Медленное движение оси Земли, прецессия , вызывает медленный, непрерывный поворот системы координат на запад вокруг полюсов эклиптики , совершая один оборот примерно за 26 000 лет. На это накладывается меньшее движение эклиптики и небольшое колебание земной оси — нутация . ^[4]

Чтобы зафиксировать точное основное направление, эти движения требуют указания точки равноденствия определенной даты, известной как эпоха , при определении положения. Наиболее часто используются три:

Среднее равноденствие стандартной эпохи (обычно J2000.0 , но может включать B1950.0, B1900.0 и т. д.): — это фиксированное стандартное направление, позволяющее напрямую сравнивать позиции, установленные в разные даты.
Среднее равноденствие даты: является пересечением эклиптики «даты» (т. е. эклиптики в ее положении в «дате») со средним экватором (т. е. экватора, повернутого за счет прецессии к своему положению в «дате», но свободного от небольших периодические колебания нутации). Обычно используется при расчете планетарных орбит .
Дата истинного равноденствия: это пересечение эклиптики «даты» с истинным экватором (то есть средним экватором плюс нутация). Это фактическое пересечение двух плоскостей в любой конкретный момент с учетом всех движений.

Таким образом, положение в экваториальной системе координат обычно указывается истинное равноденствие и экватор даты , среднее равноденствие и экватор J2000.0 или подобное. Обратите внимание, что не существует «средней эклиптики», поскольку эклиптика не подвержена небольшим периодическим колебаниям. ^[5]

Сферические координаты

Использование в астрономии

Сферические координаты звезды координаты часто выражаются парой: прямое восхождение и склонение , без расстояния . Направление достаточно удаленных объектов одинаково для всех наблюдателей, и это направление удобно задавать одними и теми же координатами для всех. Напротив, в горизонтальной системе координат положение звезды различается от наблюдателя к наблюдателю в зависимости от их положения на поверхности Земли и постоянно меняется вместе с вращением Земли.

Телескопы, оснащенные экваториальной монтировкой и установочными кругами, для поиска объектов используют экваториальную систему координат. Установка кругов в сочетании со звездной картой или эфемеридами позволяет легко наводить телескоп на известные объекты на небесной сфере.

Склонение

Символ склонения $δ$ (строчная «дельта», сокращенно DEC) измеряет угловое расстояние до объекта, перпендикулярное небесному экватору, положительное к северу и отрицательное к югу. Например, северный полюс мира имеет склонение +90°. Началом склонения является небесный экватор, который является проекцией экватора Земли на небесную сферу. Склонение аналогично земной широте . ^[6]^[7]^[8]

Прямое восхождение

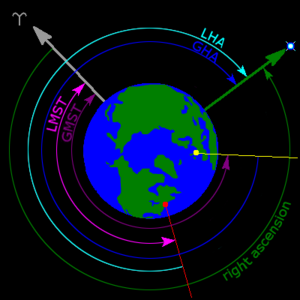
Символ прямого восхождения $α$ , (строчная «альфа», сокращенно RA) измеряет угловое расстояние объекта в восточном направлении вдоль небесного экватора от мартовского равноденствия до часового круга, проходящего через объект. Точка мартовского равноденствия — одна из двух точек, где эклиптика пересекает небесный экватор. Прямое восхождение обычно измеряется в звездных часах, минутах и секундах, а не в градусах, что является результатом метода измерения прямого восхождения путем измерения времени прохождения объектов через меридиан при вращении Земли . Есть ⁠ 360° / 24 ^час⁠ = 15° за один час прямого восхождения и 24 ^час прямого восхождения вокруг всего небесного экватора . ^[6]^[9]^[10]

При совместном использовании прямое восхождение и склонение обычно обозначаются сокращением RA/Dec.

Часовой угол

В качестве альтернативы прямому восхождению , часовой угол (сокращенно HA или LHA, местный часовой угол ), левая система, измеряет угловое расстояние объекта на запад вдоль небесного экватора наблюдателя от меридиана до часового круга, проходящего через объект. В отличие от прямого восхождения, часовой угол всегда увеличивается с вращением Земли . Часовой угол можно рассматривать как средство измерения времени с момента верхней кульминации , момента, когда объект касается меридиана над головой.

Говорят, что кульминационная звезда на меридиане наблюдателя имеет нулевой часовой угол (0 ^час). Через один сидерический час (примерно 0,9973 солнечных часа ) вращение Земли переместит звезду к западу от меридиана, и ее часовой угол составит 1 ^час. При расчете топоцентрических явлений прямое восхождение может быть преобразовано в часовой угол в качестве промежуточного шага. ^[11]^[12]^[13]

Прямоугольные координаты

Геоцентрические экваториальные координаты

Существует ряд прямоугольных вариантов экваториальных координат. У всех есть:

Начало координат в центре Земли .
Фундаментальная плоскость в плоскости земного экватора.
Основное направление ( $ось X$ ) к мартовскому равноденствию , то есть к месту, где Солнце пересекает небесный экватор в северном направлении во время своего годового видимого оборота вокруг эклиптики .
Соглашение для правшей , определяющее $ось y$ под углом 90 ° к востоку в фундаментальной плоскости и $ось z$ вдоль северной полярной оси.

Системы отсчета не вращаются вместе с Землей (в отличие от геоцентрических и фиксированных на Земле систем отсчета), оставаясь всегда направленными к равноденствию и дрейфуя во времени с движениями прецессии и нутации .

В астрономии : ^[14]
- Положение Солнца часто указывается в геоцентрических экваториальных прямоугольных координатах $X$ , $Y$ , $Z$ и четвертой координате расстояния $R$ $(= \sqrt X 2 + И 2 + Я 2)$ , в единицах астрономической единицы .
- Положения планет и других тел Солнечной системы часто указываются в геоцентрических экваториальных прямоугольных координатах $ξ$ , $η$ , $ζ$ и четвертой дистанционной координате $Δ$ (равной $\sqrt ξ 2 + ч 2 + г 2$ ), в единицах астрономической единицы .
  Эти прямоугольные координаты связаны с соответствующими сферическими координатами соотношением ${\begin{aligned}{\frac {X}{R}}={\frac {\xi }{\mathit {\Delta }}}&=\cos \delta \cos \alpha \\{\frac {Y}{R}}={\frac {\eta }{\mathit {\Delta }}}&=\cos \delta \sin \alpha \\{\frac {Z}{R}}={\frac {\zeta }{\mathit {\Delta }}}&=\sin \delta \end{aligned}}$
В астродинамике : ^[15]
- Положения искусственных спутников Земли указываются в геоцентрических экваториальных координатах, также известных как геоцентрическая экваториальная инерциальная система (GEI) , геоцентрическая инерциальная система (ECI) и традиционная инерциальная система (CIS) , которые по определению эквивалентны астрономической геоцентрической системе координат. экваториальные прямоугольные рамки вверху. В геоцентрической экваториальной системе координат $оси x$ , $y$ и $z$ часто обозначаются $I$ , $J$ и $K$ системы координат соответственно, или основа задается единичными векторами $Î$ , $Ĵ$ и $K̂$ .
- Геоцентрическая небесная система отсчета (GCRF) является геоцентрическим эквивалентом Международной небесной системы отсчета (ICRF). Его основное направление — равноденствие J2000.0 , и оно не движется с прецессией и нутацией , но в остальном эквивалентно вышеупомянутым системам.

Краткое описание обозначений астрономических экваториальных координат ^[16]
	сферический			Прямоугольный
	Прямое восхождение	Склонение	Расстояние	Общий	специального назначения
Геоцентрический	$а$	$д$	$Д$	$ξ$ , $час$ , $г$	$X$ , $Y$ , $Z$ (Вс)
гелиоцентрический				$х$ , $у$ , $я$

Гелиоцентрические экваториальные координаты

В астрономии существует также гелиоцентрический прямоугольный вариант экваториальных координат, обозначаемый $x$ , $y$ , $z$ , который имеет:

Начало координат в центре Солнца .
Фундаментальная плоскость в плоскости земного экватора.
Основное направление ( $ось X$ ) к мартовскому равноденствию .
Правостороннее под соглашение, определяющее $ось y$ углом 90 ° к востоку в фундаментальной плоскости и $ось z$ вдоль . северной полярной оси Земли

Эта система координат во всех отношениях эквивалентна $системе ξ$ , $η$ , $ζ$ , приведенной выше, за исключением того, что начало координат перенесено в центр Солнца . Он обычно используется при расчете планетарных орбит. Три астрономические прямоугольные системы координат связаны соотношением ^[17] ${\begin{aligned}\xi &=x+X\\\eta &=y+Y\\\zeta &=z+Z\end{aligned}}$

См. также

Ссылки

^ Управление морского альманаха Военно-морской обсерватории США; Управление морского альманаха Ее Величества; Королевская Гринвичская обсерватория (1961 г.). Пояснительное приложение к Астрономическим эфемеридам и Американским эфемеридам и Морскому альманаху . Канцелярский офис HM, Лондон (переиздание 1974 г.). стр. 24 , 26.
^ Валладо, Дэвид А. (2001). Основы астродинамики и приложения . Microcosm Press, Эль-Сегундо, Калифорния. п. 157. ИСБН 1-881883-12-4 .
^ Офис морского альманаха Военно-морской обсерватории США; Гидрографическое управление Великобритании; Управление морского альманаха Ее Величества (2008). Астрономический альманах на 2010 год . Правительство США. Типография. п. М2, «видимое место». ISBN 978-0-7077-4082-9 .
^ Пояснительное приложение (1961), стр. 20, 28.
^ Меус, Жан (1991). Астрономические алгоритмы . Willmann-Bell, Inc., Ричмонд, Вирджиния. п. 137. ИСБН 0-943396-35-2 .
^ Jump up to: ^а ^б Питер Даффет-Смит (1988). Практическая астрономия с калькулятором, третье издание . Издательство Кембриджского университета . стр. 28–29 . ISBN 0-521-35699-7 .
^ Меир Х. Дегани (1976). Астрономия стала проще . Doubleday & Company, Inc. с. 216 . ISBN 0-385-08854-Х .
^ Астрономический альманах 2010 , с. М4
^ Моултон, Форест Рэй (1918). Введение в астрономию . п. 127.
^ Астрономический альманах 2010 , с. М14
^ Питер Даффет-Смит (1988). Практическая астрономия с калькулятором, третье издание . Издательство Кембриджского университета. стр. 34–36 . ISBN 0-521-35699-7 .
^ Астрономический альманах 2010 , с. М8
^ Валладо (2001), с. 154
^ Пояснительное приложение (1961), стр. 24–26.
^ Валладо (2001), стр. 157, 158
^ Пояснительное приложение (1961), разд. 1G
^ Пояснительное приложение (1961), стр. 20, 27.

Внешние ссылки

ИЗМЕРЕНИЕ НЕБА Краткое руководство по небесной сфере Джеймс Б. Калер, Университет Иллинойса
Небесная экваториальная система координат Университет Небраски-Линкольн
Исследователи небесно-экваториальных координат Университет Небраски-Линкольн

[1] Управление морского альманаха Военно-морской обсерватории США; Управление морского альманаха Ее Величества; Королевская Гринвичская обсерватория (1961 г.). Пояснительное приложение к Астрономическим эфемеридам и Американским эфемеридам и Морскому альманаху . Канцелярский офис HM, Лондон (переиздание 1974 г.). стр. 24 , 26.

[Vallado-2] Валладо, Дэвид А. (2001). Основы астродинамики и приложения . Microcosm Press, Эль-Сегундо, Калифорния. п. 157. ИСБН 1-881883-12-4 .

[3] Офис морского альманаха Военно-морской обсерватории США; Гидрографическое управление Великобритании; Управление морского альманаха Ее Величества (2008). Астрономический альманах на 2010 год . Правительство США. Типография. п. М2, «видимое место». ISBN 978-0-7077-4082-9 .

[4] Пояснительное приложение (1961), стр. 20, 28.

[5] Меус, Жан (1991). Астрономические алгоритмы . Willmann-Bell, Inc., Ричмонд, Вирджиния. п. 137. ИСБН 0-943396-35-2 .

[calculator28-6] Jump up to: ^а ^б Питер Даффет-Смит (1988). Практическая астрономия с калькулятором, третье издание . Издательство Кембриджского университета . стр. 28–29 . ISBN 0-521-35699-7 .

[simple-7] Меир Х. Дегани (1976). Астрономия стала проще . Doubleday & Company, Inc. с. 216 . ISBN 0-385-08854-Х .

[8] Астрономический альманах 2010 , с. М4

[9] Моултон, Форест Рэй (1918). Введение в астрономию . п. 127.

[10] Астрономический альманах 2010 , с. М14

[11] Питер Даффет-Смит (1988). Практическая астрономия с калькулятором, третье издание . Издательство Кембриджского университета. стр. 34–36 . ISBN 0-521-35699-7 .

[12] Астрономический альманах 2010 , с. М8

[13] Валладо (2001), с. 154

[14] Пояснительное приложение (1961), стр. 24–26.

[15] Валладо (2001), стр. 157, 158

[16] Пояснительное приложение (1961), разд. 1G

[17] Пояснительное приложение (1961), стр. 20, 27.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]