Ленгмюровский зонд

Один из двух зондов Ленгмюра Шведского института космической физики в Уппсале на борту ЕКА космического корабля «Розетта» , который вращался вокруг кометы и столкнулся с ней . Зонд представляет собой сферическую часть диаметром 50 мм , изготовленную из титана с поверхностным покрытием из нитрида титана .

Зонд Ленгмюра — это устройство, используемое для определения температуры электронов, плотности электронов и электрического потенциала плазмы . Он работает путем введения одного или нескольких электродов в плазму с постоянным или изменяющимся во времени электрическим потенциалом между различными электродами или между ними и окружающим сосудом. Измеренные токи и потенциалы в этой системе позволяют определять физические свойства плазмы.

IV дебаевской

Началом теории зондов Ленгмюра является ВАХ , то есть плотность тока , дебаевского слоя текущего к поверхности в плазме, как функция падения напряжения на слое. Представленный здесь анализ показывает, как электронная температура, электронная плотность и потенциал плазмы могут быть получены из ВАХ . В некоторых ситуациях более детальный анализ может дать информацию о плотности ионов ( $n_{i}$), ионная температура $T_{i}$ электронов по энергии , или функция распределения (ФРЭЭЭ), или $f_{e}(v)$.

Плотность тока насыщения ионов

Рассмотрим сначала поверхность, на которую действует большое отрицательное напряжение. Если напряжение достаточно велико, практически все электроны (и любые отрицательные ионы) будут отталкиваться. Скорость ионов будет удовлетворять критерию оболочки Бома , который, строго говоря, является неравенством, но обычно выполняется незначительно. Критерий Бома в своей предельной форме говорит, что скорость ионов на краю оболочки — это просто скорость звука, определяемая выражением

$c_{s}={\sqrt {k_{B}(ZT_{e}+\gamma _{i}T_{i})/m_{i}}}$.

Слагаемым ионной температуры часто пренебрегают, что оправдано, если ионы холодные. Z - (среднее) зарядовое состояние ионов, а $\gamma _{i}$ – коэффициент адиабаты для ионов. Правильный выбор $\gamma _{i}$ является предметом некоторых разногласий. В большинстве анализов используются $\gamma _{i}=1$, что соответствует изотермическим ионам, но некоторые кинетические теории предполагают, что $\gamma _{i}=3$. Для $Z=1$ и $T_{i}=T_{e}$, использование большего значения приводит к выводу, что плотность равна ${\sqrt {2}}$ раз меньше. Неопределенности такого масштаба возникают в нескольких местах при анализе данных зонда Ленгмюра, и их очень трудно устранить.

Плотность заряда ионов зависит от зарядового состояния Z , но квазинейтральность позволяет записать ее просто через плотность электронов как $q_{e}n_{e}$, где $q_{e}$ - заряд электрона и $n_{e}$ - плотность электронов.

Используя эти результаты, мы получаем плотность тока к поверхности, обусловленную ионами. Плотность тока при больших отрицательных напряжениях обусловлена ​​исключительно ионами и, за исключением возможных эффектов расширения оболочки, не зависит от напряжения смещения, поэтомуназывается плотностью тока насыщения ионов и определяется выражением

$j_{i}^{max}=q_{e}n_{e}c_{s}$ где $c_{s}$ такое, как определено выше.

Параметры плазмы, в частности плотность, такие же, как у края слоя.

электронный

По мере уменьшения напряжения дебаевского слоя более энергичные электроны способны преодолеть потенциальный барьер электростатического слоя. Мы можем смоделировать электроны на краю слоя с распределением Максвелла – Больцмана , т.е.

$f(v_{x})\,dv_{x}\propto e^{-{\frac {1}{2}}m_{e}v_{x}^{2}/k_{B}T_{e}}$,

за исключением того, что хвост высокой энергии, удаляющийся от поверхности, отсутствует, потому что отражаются только электроны с более низкой энергией, движущиеся к поверхности. Электроны с более высокой энергией преодолевают потенциал оболочки и поглощаются. Средняя скорость электронов, способных преодолеть напряжение оболочки, равна

$\langle v_{e}\rangle ={\frac {\int _{v_{e0}}^{\infty }f(v_{x})\,v_{x}\,dv_{x}}{\int _{-\infty }^{\infty }f(v_{x})\,dv_{x}}}$,

где скорость обрезания верхнего интеграла равна

$v_{e0}={\sqrt {2q_{e}\Delta V/m_{e}}}$.

$\Delta V$ – напряжение на дебаевском слое, то есть потенциал на краю слоя минус потенциал поверхности. Для большого напряжения по сравнению с температурой электронов результат

$\langle v_{e}\rangle ={\sqrt {\frac {k_{B}T_{e}}{2\pi m_{e}}}}\,e^{-q_{e}\Delta V/k_{B}T_{e}}$.

Используя это выражение, мы можем записать электронный вклад в ток зонда через ток насыщения ионов как

$j_{e}=j_{i}^{max}{\sqrt {m_{i}/2\pi m_{e}}}\,e^{-q_{e}\Delta V/k_{B}T_{e}}$,

действителен до тех пор, пока ток электронов не более чем в два или три раза превышает ток ионов.

Плавающий потенциал

Полный ток, конечно, представляет собой сумму ионного и электронного токов:

$j=j_{i}^{max}\left(-1+{\sqrt {m_{i}/2\pi m_{e}}}\,e^{-q_{e}\Delta V/k_{B}T_{e}}\right)$.

Мы исходим из того, что ток с поверхности в плазму положителен. Интересным и практическим вопросом является потенциал поверхности, по которой не течет чистый ток. Из приведенного выше уравнения легко видеть, что

$\Delta V=(k_{B}T_{e}/q_{e})\,(1/2)\ln(m_{i}/2\pi m_{e})$.

Если ввести приведенную массу иона $\mu _{i}=m_{i}/m_{e}$, мы можем написать

$\Delta V=(k_{B}T_{e}/q_{e})\,(2.8+0.5\ln \mu _{i})$

Поскольку плавающий потенциал является экспериментально доступной величиной, ток (ниже электронного насыщения) обычно записывается как

$j=j_{i}^{max}\left(-1+\,e^{q_{e}(V_{0}-\Delta V)/k_{B}T_{e}}\right)$.

ток

Когда потенциал электрода равен потенциалу плазмы или превышает его, оболочка, отражающая электроны, больше не существует, и ток электронов насыщается. Используя приведенное выше выражение Больцмана для средней скорости электрона с $v_{e0}=0$ и установив ионный ток равным нулю, плотность тока насыщения электронов будет равна

$j_{e}^{max}=j_{i}^{max}{\sqrt {m_{i}/\pi m_{e}}}=j_{i}^{max}\left(24.2\,{\sqrt {\mu _{i}}}\right)$

Хотя это выражение обычно используется при теоретических обсуждениях ленгмюровских зондов, его вывод не является строгим, а экспериментальная база слабой. Теория двойных слоев обычно использует выражение, аналогичное критерию Бома , но с поменянными ролями электронов и ионов, а именно

$j_{e}^{max}=q_{e}n_{e}{\sqrt {k_{B}(\gamma _{e}T_{e}+T_{i})/m_{e}}}=j_{i}^{max}{\sqrt {m_{i}/m_{e}}}=j_{i}^{max}\left(42.8\,{\sqrt {\mu _{i}}}\right)$

где численное значение было найдено путем принятия T _i = T _e и γ _i =γ _e .

На практике экспериментальное измерение тока насыщения электронами зачастую затруднительно и обычно считается неинформативным. При измерении оказывается, что оно сильно варьируется и, как правило, намного ниже (в три и более раз), чем значение, указанное выше. Часто четкой насыщенности вообще не видно. Понимание электронного насыщения является одной из важнейших нерешенных проблем теории зондов Ленгмюра.

объемной

Теория оболочек Дебая объясняет основное поведение ленгмюровских зондов, но не является полной. Простое введение объекта, например зонда, в плазму меняет плотность, температуру и потенциал на краю оболочки и, возможно, повсюду. Изменение напряжения на зонде также, как правило, приводит к изменению различных параметров плазмы. Такие эффекты менее изучены, чем физика оболочек, но их можно, по крайней мере, в некоторых случаях грубо объяснить.

Предварительная оболочка

Критерий Бома требует, чтобы ионы входили в дебаевскую оболочку со скоростью звука. Потенциальный перепад, который разгоняет их до этой скорости, называется предоболочкой . Он имеет пространственный масштаб, который зависит от физики источника ионов, но велик по сравнению с дебаевской длиной и часто порядка размеров плазмы. Величина падения потенциала равна (не менее)

$\Phi _{pre}={\frac {{\frac {1}{2}}m_{i}c_{s}^{2}}{Ze}}=k_{B}(T_{e}+Z\gamma _{i}T_{i})/(2Ze)$

Ускорение ионов влечет за собой и уменьшение плотности, обычно примерно в 2 раза в зависимости от деталей.

Сопротивление

Столкновения между ионами и электронами также будут влиять на ВАХ ленгмюровского зонда. Когда электрод смещен на любое напряжение, кроме плавающего потенциала, ток, который он потребляет, должен проходить через плазму, которая имеет конечное удельное сопротивление. Удельное сопротивление и путь тока можно относительно легко рассчитать в ненамагниченной плазме. В замагниченной плазме задача гораздо сложнее. В любом случае эффект заключается в добавлении падения напряжения, пропорционального потребляемому току, что приводит к сдвигу характеристики. Отклонение от экспоненциальной функции обычно невозможно наблюдать непосредственно, поэтому уплощение характеристики обычно ошибочно интерпретируется как увеличение температуры плазмы. Глядя на это с другой стороны, любую измеренную ВАХ можно интерпретировать как горячую плазму, где большая часть напряжения падает в дебаевском слое, или как холодную плазму, где большая часть напряжения падает в объемной плазме. Без количественного моделирования объемного удельного сопротивления зонды Ленгмюра могут дать только верхний предел электронной температуры.

Расширение оболочки

Недостаточно знать плотность тока как функцию напряжения смещения, поскольку измеряется . абсолютный ток В ненамагниченной плазме за площадь сбора тока обычно принимают площадь открытой поверхности электрода. В замагниченной плазме за проекционную площадь берется площадь электрода, если смотреть вдоль магнитного поля. Если электрод не затенен стеной или другим близлежащим предметом, то площадь необходимо увеличить вдвое, чтобы учесть ток, идущий по полю с обеих сторон. Если размеры электрода не малы по сравнению с дебаевской длиной, то размер электрода эффективно увеличивается во всех направлениях на толщину оболочки. В замагниченной плазме иногда полагают, что электрод аналогичным образом увеличивается на ионный ларморовский радиус .

Конечный ларморовский радиус позволяет некоторым ионам достигать электрода, которые в противном случае прошли бы мимо него. Детали эффекта не были рассчитаны полностью последовательным образом.

Если мы будем называть область зонда, включающую эти эффекты, как $A_{eff}$ (которое может быть функцией напряжения смещения) и сделать предположения

• $T_{i}=T_{e}$,
• $Z=1$
• $\gamma _{i}=3$, и
• $n_{e,sh}=0.5\,n_{e}$,

и игнорировать последствия

• объемное удельное сопротивление и
• электронное насыщение,

тогда ВАХ станет

$I=I_{i}^{max}(-1+e^{q_{e}(V_{pr}-V_{fl})/(k_{B}T_{e})})$,

где

$I_{i}^{max}=q_{e}n_{e}{\sqrt {k_{B}T_{e}/m_{i}}}\,A_{eff}$.

Намагниченная плазма

Теория ленгмюровских зондов гораздо сложнее, когда плазма намагничена. Простейшее расширение ненамагниченного случая — просто использовать проецируемую площадь, а не площадь поверхности электрода. Для длинного цилиндра, удаленного от других поверхностей, это уменьшает эффективную площадь в π/2 = 1,57 раза. Как упоминалось ранее, может потребоваться увеличить радиус примерно на ларморовский радиус теплового иона, но не выше эффективной площади для ненамагниченного случая.

Использование проецируемой площади, по-видимому, тесно связано с существованием магнитной оболочки . Его масштаб представляет собой ларморовский радиус иона при скорости звука, который обычно находится между масштабами дебаевского и предслоя. Критерий Бома для ионов, входящих в магнитный слой, применим к движению вдоль поля, а на входе в дебаевский слой — к движению нормально к поверхности. Это приводит к уменьшению плотности на синус угла между полем и поверхностью. Сопутствующее увеличение дебаевской длины необходимо учитывать при рассмотрении ионной ненасыщенности из-за эффектов оболочки.

Особенно интересна и сложна для понимания роль токов перекрестного поля. Наивно можно было бы ожидать, что ток будет параллелен магнитному полю вдоль силовой трубки . Во многих геометриях эта силовая трубка заканчивается на поверхности в удаленной части устройства, и это пятно само должно иметь ВАХ . Конечным результатом будет измерение характеристики двойного зонда; другими словами, ток насыщения электронов равен току насыщения ионов.

Если рассмотреть эту картину подробно, то видно, что силовая трубка должна заряжаться, а окружающая плазма должна вращаться вокруг нее. Ток, входящий в магнитную трубку или выходящий из нее, должен быть связан с силой, замедляющей это вращение. Возможными силами являются вязкость, трение с нейтралами и силы инерции, связанные с потоками плазмы, как постоянными, так и колеблющимися. На практике неизвестно, какая сила является самой сильной, и на самом деле обычно трудно найти какую-либо силу, которая была бы достаточно мощной, чтобы объяснить фактически измеряемые характеристики.

Вероятно также, что магнитное поле играет решающую роль в определении уровня электронного насыщения, но количественной теории пока не существует.

Конфигурации электродов

Если у вас есть теория ВАХ электрода , можно приступить к ее измерению, а затем согласовать данные с теоретической кривой для определения параметров плазмы. Самый простой способ сделать это — развертка напряжения на одном электроде, но по ряду причин на практике используются схемы, использующие несколько электродов или исследующие только часть характеристики.

Одиночный зонд

Самый простой способ измерения ВАХ плазмы — с помощью одного зонда , состоящего из одного электрода, смещенного с наклоном напряжения относительно сосуда. Достоинствами являются простота электрода и избыточность информации, т.е. можно проверить, имеет ли ВАХ ожидаемый вид. Потенциально дополнительная информация может быть извлечена из деталей характеристики. Недостатками являются более сложная электроника смещения и измерения, а также плохое временное разрешение. Если флуктуации присутствуют (а они всегда есть) и развертка медленнее, чем частота флуктуаций (как это обычно бывает), то IV представляет собой средний ток как функцию напряжения, что может привести к систематическим ошибкам, если его анализировать как хотя это была мгновенная капельница . Идеальная ситуация — качать напряжение на частоте выше частоты флуктуаций, но все же ниже ионной циклотронной частоты. Однако это требует сложной электроники и большой осторожности.

Двойной зонд

Электрод может быть смещен относительно второго электрода, а не относительно земли. Теория аналогична теории одиночного зонда, за исключением того, что ток ограничен током насыщения ионов как для положительного, так и для отрицательного напряжения. В частности, если $V_{bias}$ – напряжение, приложенное между двумя одинаковыми электродами, ток определяется выражением;

$I=I_{i}^{max}\left(-1+\,e^{q_{e}(V_{2}-V_{fl})/k_{B}T_{e}}\right)=-I_{i}^{max}\left(-1+\,e^{q_{e}(V_{1}-V_{fl})/k_{B}T_{e}}\right)$,

который можно переписать с помощью $V_{bias}=V_{2}-V_{1}$ как гиперболический тангенс :

$I=I_{i}^{max}\tanh \left({\frac {1}{2}}\,{\frac {q_{e}V_{bias}}{k_{B}T_{e}}}\right)$.

Одним из преимуществ двойного зонда является то, что ни один из электродов никогда не находится слишком высоко над плавающим слоем, что позволяет избежать теоретических неопределенностей при больших токах электронов. Если требуется отобрать больше экспоненциальной электронной части характеристики, можно использовать асимметричный двойной зонд , у которого один электрод больше другого. Если соотношение площадей сбора больше, чем квадратный корень из отношения масс ионов и электронов, то такое расположение эквивалентно зонду с одним наконечником. Если соотношение площадей сбора не так велико, то характеристика будет промежуточной между симметричной конфигурацией с двойным наконечником и конфигурацией с одним наконечником. Если $A_{1}$ - площадь большего кончика, тогда:

$I=A_{1}J_{i}^{max}\left[\coth \left({\frac {q_{e}V_{bias}}{2k_{B}T_{e}}}\right)+{\frac {\left({\frac {A_{1}}{A_{2}}}-1\right)\,e^{-q_{e}V_{bias}/2k_{B}T_{e}}}{2\sinh \left({\frac {q_{e}V_{bias}}{2k_{B}T_{e}}}\right)}}\right]^{-1}$

Еще одним преимуществом является отсутствие привязки к сосуду, поэтому он в некоторой степени невосприимчив к возмущениям в радиочастотной плазме. С другой стороны, он имеет те же ограничения, что и одиночный зонд, связанные со сложной электроникой и плохим временным разрешением. Кроме того, второй электрод не только усложняет систему, но и делает ее подверженной возмущениям градиентами плазмы.

Тройной зонд

Элегантная конфигурация электродов — тройной зонд. Состоит из двух электродов, находящихся под постоянным напряжением, и третьего, плавающего. Напряжение смещения выбирается в несколько раз больше температуры электронов, чтобы отрицательный электрод потреблял ток насыщения ионов, который, как и плавающий потенциал, измеряется напрямую. Общее эмпирическое правило для этого смещения напряжения составляет 3/e раза от ожидаемой температуры электронов. Поскольку конфигурация смещенного наконечника является плавающей, положительный зонд может поглощать не более электронного тока, равного по величине и противоположного по полярности ионному току насыщения, потребляемому отрицательным зондом, определяемому формулой:

$-I_{+}=I_{-}=I_{i}^{max}$

и, как и раньше, плавающий наконечник практически не потребляет ток:

$I_{fl}=0$.

Предполагая, что: 1.) Распределение электронов по энергии в плазме максвелловское,2.) Средняя длина свободного пробега электронов больше, чем ионная оболочка вокруг кончиков, и больше, чем радиус зонда, и3.) размеры оболочки зонда намного меньше расстояния между зондами,тогда ток любого зонда можно рассматривать состоящим из двух частей – высокоэнергетического хвоста максвелловского распределения электронов и тока насыщения ионов:

$I_{probe}=-I_{e}e^{-q_{e}V_{probe}/(kT_{e})}+I_{i}^{max}$

где ток I _e – тепловой ток. Конкретно,

$I_{e}=SJ_{e}=Sn_{e}q_{e}{\sqrt {kT_{e}/2\pi m_{e}}}$,

где S — площадь поверхности, J _e — плотность электронного тока, а n _e — плотность электронов.

Если предположить, что ток насыщения ионов и электронов одинаков для каждого зонда, то формулы для тока на каждом из наконечников зонда примут вид

$I_{+}=-I_{e}e^{-q_{e}V_{+}/(kT_{e})}+I_{i}^{max}$

$I_{-}=-I_{e}e^{-q_{e}V_{-}/(kT_{e})}+I_{i}^{max}$

$I_{fl}=-I_{e}e^{-q_{e}V_{fl}/(kT_{e})}+I_{i}^{max}$.

Тогда просто показать

$\left(I_{+}-I_{fl})/(I_{+}-I_{-}\right)=\left(1-e^{-q_{e}(V_{fl}-V_{+})/(kT_{e})}\right)/\left(1-e^{-q_{e}(V_{-}-V_{+})/(kT_{e})}\right)$

но соотношения выше, указывающие, что I ₊ =-I ₋ и I _fl =0, дают

$1/2=\left(1-e^{-q_{e}(V_{fl}-V_{+})/(kT_{e})}\right)/\left(1-e^{-q_{e}(V_{-}-V_{+})/(kT_{e})}\right)$,

трансцендентное уравнение в терминах приложенного и измеренного напряжения и неизвестного T _e, которое в пределе q _e V _Bias = q _e (V ₊ -V ₋ ) >> k T _e , становится

$(V_{+}-V_{fl})=(k_{B}T_{e}/q_{e})\ln 2$.

То есть разница напряжений между положительным и плавающим электродами пропорциональна температуре электронов. (Это было особенно важно в шестидесятые и семидесятые годы, когда сложные методы обработки данных не стали широко доступны.)

Более сложный анализ данных тройного зондирования может учитывать такие факторы, как неполное насыщение, ненасыщение, неравные площади.

Преимущество тройных датчиков заключается в простой смещающей электронике (не требуется развертка), простом анализе данных, превосходном временном разрешении и нечувствительности к потенциальным флуктуациям (будь то вызванные источником радиочастотных сигналов или собственные флуктуации). Как и двойные зонды, они чувствительны к градиентам параметров плазмы.

Особые договоренности

схемы с четырьмя ( тетра-зондами ) или пятью ( пента-зондами Иногда использовались ), но преимущество перед тройными зондами никогда не было полностью убедительным. Расстояние между зондами должно быть больше, чем дебаевская длина плазмы, чтобы предотвратить перекрытие дебаевской оболочки .

Зонд со штифтовой пластиной состоит из небольшого электрода, расположенного непосредственно перед большим электродом. Идея состоит в том, что развертка напряжения большого зонда может нарушить потенциал плазмы на краю оболочки и тем самым усугубить трудность интерпретации ВАХ . Плавающий потенциал маленького электрода можно использовать для корректировки изменений потенциала на краю оболочки большого зонда. Экспериментальные результаты этой схемы выглядят многообещающе, но сложность эксперимента и остаточные трудности в интерпретации не позволили этой конфигурации стать стандартной.

были предложены различные геометрии Для использования в качестве зондов ионной температуры , например, два цилиндрических наконечника, которые вращаются друг вокруг друга в намагниченной плазме. Поскольку эффекты затенения зависят от ларморовского радиуса иона, результаты можно интерпретировать в терминах ионной температуры. Ионная температура — важная величина, которую очень трудно измерить. К сожалению, очень сложно анализировать такие исследования полностью согласованным образом.

В эмиссионных зондах используется электрод, нагреваемый либо электрически, либо за счет воздействия плазмы. Когда электрод смещен более положительно, чем потенциал плазмы, испускаемые электроны оттягиваются обратно на поверхность, поэтому ВАХ не практически изменяется . Как только электрод смещен отрицательно по отношению к потенциалу плазмы, эмитированные электроны отталкиваются и создают большой отрицательный ток. Возникновение этого тока или, точнее, возникновение несоответствия характеристик ненагретого и нагретого электрода является чувствительным индикатором потенциала плазмы.

Для измерения флуктуаций параметров плазмы используются массивы электродов, обычно одномерные, но иногда и двумерные. Типичная решетка имеет интервал 1 мм и в общей сложности 16 или 32 электрода. Более простым устройством для измерения флуктуаций является электрод с отрицательным смещением, окруженный двумя плавающими электродами. Ток ионного насыщения рассматривается как заменитель плотности, а плавающий потенциал - как заменитель потенциала плазмы. Это позволяет грубо измерить турбулентный поток частиц.

$\Phi _{turb}=\langle {\tilde {n}}_{e}{\tilde {v}}_{E\times B}\rangle \propto \langle {\tilde {I}}_{i}^{max}({\tilde {V}}_{fl,2}-{\tilde {V}}_{fl,1})\rangle$

зонд Ленгмюра в

Чаще всего зонд Ленгмюра представляет собой электрод небольшого размера, вставленный в плазму и подключенный к внешней цепи, измеряющей свойства плазмы по отношению к земле. Заземление обычно представляет собой электрод с большой площадью поверхности и обычно контактирует с той же плазмой (очень часто с металлической стенкой камеры). Это позволяет зонду измерять ВАХ плазмы. Зонд измеряет характеристический ток $i(V)$ плазмы, когда зонд смещен потенциалом $V$.

Рис. 1. Иллюстрация вывода характеристики Ленгмюровского зонда IV.

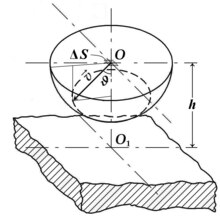
зонда Связь между ВАХ и параметрами изотропной плазмы была найдена Ирвингом Ленгмюром. и наиболее элементарно их можно вывести для плоского зонда большой площади поверхности. $S_{z}$ (игнорируя проблему краевых эффектов). Давайте выберем точку $O$ в плазме на расстоянии $h$ от поверхности зонда, где электрическое поле зонда незначительно, а каждый электрон плазмы, проходящий через эту точку, мог бы достичь поверхности зонда без столкновений с компонентами плазмы: $\lambda _{D}\ll \lambda _{Te}$, $\lambda _{D}$ - длина Дебая и $\lambda _{Te}$ – длина свободного пробега электрона, рассчитанная для его полного сечения с плазменными компонентами. В окрестностях точки $O$ мы можем представить себе небольшой элемент площади поверхности $\Delta S$ параллельно поверхности зонда. Элементарный ток $di$ электронов плазмы, проходящих через $\Delta S$ в направлении поверхности зонда можно записать в виде

$di=q_{e}\Delta Sdn(v,\vartheta )v\cos \vartheta$, ( 1 )

где $v$ является скаляром вектора тепловой скорости электрона ${\vec {v}}$,

$dn(v,\vartheta )=nf(v){\frac {2\pi \sin \vartheta }{4\pi }}dvd\vartheta$, ( 2 )

$2\pi \sin \vartheta d\vartheta$ — элемент телесного угла с его относительным значением $2\pi \sin \vartheta d\vartheta /4\pi$, $\vartheta$ угол между перпендикуляром к поверхности зонда, отведенным из точки $O$ и радиус-вектор тепловой скорости электрона ${\vec {v}}$ образуя сферический слой толщиной $dv$ в пространстве скоростей и $f(v)$ – функция распределения электронов, нормированная на единицу

$\int \limits _{0}^{\infty }f(v)dv=1$. ( 3 )

Учитывая однородность условий вдоль поверхности зонда (границы исключены), $\Delta S\rightarrow S_{z}$, мы можем взять двойной интеграл по углу $\vartheta$, а по скорости $v$, из выражения ( 1 ), после замены Ур. ( 2 ) в нем для расчета полного электронного тока на зонде

$i(v)=q_{e}nS_{z}{\frac {1}{4\pi }}\int \limits _{\sqrt {2q_{e}V/m}}^{\infty }f(v)dv\int \limits _{0}^{\zeta }v\cos \vartheta 2\pi \sin \vartheta d\vartheta$. ( 4 )

где $V$ – зондовый потенциал по отношению к потенциалу плазмы $V=0$, ${\sqrt {2q_{e}V/m}}$ - наименьшее значение скорости электрона, при котором электрон все еще может достичь поверхности зонда, заряженной до потенциала $V$, $\zeta$ является верхней границей угла $\vartheta$ при котором электрон, имеющий начальную скорость $v$ все еще может достичь поверхности зонда с нулевым значением своей скорости на этой поверхности. Это означает, что значение $\zeta$ определяется условием

$v\cos \zeta ={\sqrt {2q_{e}V/m}}$. ( 5 )

Получение значения $\zeta$ из уравнения. ( 5 ) и подставив его в уравнение. ( 4 ) можно получить зондовую ВАХ (в пренебрежении ионным током) в диапазоне зондового потенциала $-\infty <V\leq 0$ в форме

$i(V)={\frac {q_{e}nS_{z}}{4}}\int \limits _{\sqrt {2q_{e}V/m}}^{\infty }f(v)\left(1-{\frac {2q_{e}V}{mv^{2}}}\right)vdv$. ( 6 )

Дифференцирующее уравнение. ( 6 ) дважды по потенциалу $V$ зонда , можно найти выражение, описывающее вторую производную IV характеристики (полученную впервые М. Дж. Дрювестейном

$i^{\prime \prime }(V)={\frac {q_{e}^{2}nS_{z}}{4m}}{\frac {1}{V}}f\left({\sqrt {2q_{e}V/m}}\right)$ ( 7 )

определение функции распределения электронов по скорости $f\left({\sqrt {2q_{e}V/m}}\right)$ в явной форме. MJ Druyvestein показал, в частности, что уравнения. ( 6 ) и ( 7 ) справедливы для описания работы зонда любой произвольной выпуклой геометрической формы. Подставляя максвелловскую функцию распределения :

$f^{(0)}(v)={\frac {4}{\sqrt {\pi }}}{\frac {v^{2}}{v_{p}^{3}}}\exp \left(-v^{2}/v_{p}^{2}\right)$, ( 8 )

где $v_{p}=\langle v\rangle {\sqrt {\pi }}/2$ — наиболее вероятная скорость в уравнении. ( 6 ) получаем выражение

$i^{(0)}(V)={\frac {q_{e}n\langle v\rangle }{4}}S_{z}\exp \left(-q_{e}V/{\mathcal {E}}_{p}\right)$. ( 9 )

Рис. 2. IV характеристика ленгмюровского зонда в изотропной плазме

Отсюда следует весьма полезное на практике соотношение

$\ln \left(i^{(0)}(V)/i^{(0)}(0)\right)=-q_{e}V/{\mathcal {E}}_{p}$. ( 10 )

позволяющий получить энергию электрона ${\mathcal {E}}_{p}=k_{B}T$ (только для максвелловской функции распределения!) по наклону ВАХ зонда в полулогарифмическом масштабе. Таким образом, в плазме с изотропным распределением электронов электронный ток $i_{th}(0)$ на поверхности $S_{z}=2\pi r_{z}l_{z}$ цилиндрического ленгмюровского зонда при потенциале плазмы $V=0$ определяется средней тепловой скоростью электронов $\langle v\rangle$ и может быть записано в виде уравнения (см. уравнения ( 6 ), ( 9 ) при $V=0$)

$i_{th}(0)=q_{e}n\langle v\rangle {\frac {1}{4}}\times 2\pi r_{z}l_{z}$, ( 11 )

где $n$ концентрация электронов, $r_{z}$ – радиус зонда, а $l_{z}$ это его длина. Очевидно, что если электроны плазмы образуют электронный ( поток ) поперек оси цилиндрического ветер зонда со скоростью $v_{d}\gg \langle v\rangle$, выражение

$i_{d}=env_{d}\times 2r_{z}l_{z}$ ( 12 )

соответствует действительности. В плазме, создаваемой газоразрядными дуговыми источниками, а также источниками с индуктивной связью, электронный ветер может развивать число Маха $M^{(0)}=v_{d}/\langle v\rangle =({\sqrt {\pi }}/2)\alpha \gtrsim 1$ . Здесь параметр $\alpha$ вводится вместе с числом Маха для упрощения математических выражений. Обратите внимание, что $({\sqrt {\pi }}/2)\langle v\rangle =v_{p}$, где $v_{p}$ — наиболее вероятная скорость для максвелловской функции распределения , так что $\alpha =v_{d}/v_{p}$ . Таким образом, общий случай, когда $\alpha \gtrsim 1$ представляет теоретический и практический интерес. Соответствующие физико-математические соображения, изложенные в работах В [9,10] было показано, что при максвелловской функции распределения электронов в системе отсчета, движущихся со скоростью $v_{d}$ поперек оси цилиндрического зонда, установленного под потенциалом плазмы $V=0$, ток электронов на зонде можно записать в виде

Рис.3. IV Характеристика цилиндрического зонда при скрещивающемся электронном ветре

${\frac {i(0)}{enS_{z}}}={\frac {\langle v\rangle }{4}}\exp(-\alpha ^{2}/2)I_{0}(\alpha ^{2}/2)\left(1+\alpha ^{2}\left(1+I_{1}(\alpha ^{2}/2)/I_{0}(\alpha ^{2}/2)\right)\right)$, ( 13 )

где $I_{0}$ и $I_{1}$ являются функциями Бесселя мнимых аргументов и уравнением. ( 13 ) сводится к уравнению. ( 11 ) в $\alpha \rightarrow 0$ сводится к уравнению ( 12 ) в $\alpha \rightarrow \infty$ . Вторая производная ВАХ щупа $i^{\prime \prime }(V)$ относительно потенциала зонда $V$ можно представить в этом случае в виде (см. рис. 3)

$i^{\prime \prime }(x)=enS_{z}{\frac {v_{p}}{2\pi ^{3/2}({\mathcal {E}}_{p}/e)^{2}}}{\frac {1}{\sqrt {x}}}\int \limits _{0}^{\pi }({\sqrt {x}}-\cos \varphi )\exp \left(-\alpha ^{2}({\sqrt {x}}-\cos \varphi )\right)d\varphi$, ( 14 )

где

$x={\frac {1}{\alpha ^{2}}}{\frac {V}{{\mathcal {E}}_{p}/e}}$ ( 15 )

и энергия электрона ${\mathcal {E}}_{p}/e$ выражается в эВ.

Все параметры электронной заселенности: $n$, $\alpha$, $\langle v\rangle$ и $v_{p}$ в плазме можно получить из второй производной IV характеристики экспериментального зонда $i^{\prime \prime }(V)$ по наилучшему совпадению метода наименьших квадратов с теоретической кривой, выраженной уравнением. ( 14 ). Подробности и задачу общего случая немаксвелловских функций распределения электронов см. ^,

соображения

Для лабораторной и технической плазмы электроды чаще всего представляют собой вольфрамовую или танталовую проволоку толщиной в несколько тысячных дюйма, поскольку они имеют высокую температуру плавления, но могут быть сделаны достаточно маленькими, чтобы не возмущать плазму. Хотя температура плавления несколько ниже, иногда используют молибден , поскольку его легче обрабатывать и паять, чем вольфрам. Для термоядерной плазмы обычно используют графитовые электроды размерами от 1 до 10 мм, поскольку они выдерживают самые высокие силовые нагрузки (также сублимируя при высоких температурах, а не плавясь) и приводят к уменьшению тормозного излучения (по отношению к металлам) за счет низкий атомный номер углерода. Поверхность электрода, подвергающаяся воздействию плазмы, должна быть определена, например, путем изоляции всего, кроме кончика проволочного электрода. Если возможны значительные отложения проводящих материалов (металлов или графита), то изолятор следует отделить от электрода меандром . во избежание короткого замыкания.

В замагниченной плазме, по-видимому, лучше всего выбирать размер зонда, в несколько раз превышающий ларморовский радиус иона. Спорным является вопрос о том, лучше ли использовать гордые зонды , у которых угол между магнитным полем и поверхностью составляет не менее 15°, или зонды скрытого монтажа , которые встраиваются в обращенные к плазме компоненты и обычно имеют угол от 1 до 5°. Многие физики плазмы чувствуют себя более комфортно с гордыми зондами, которые имеют более давнюю традицию и, возможно, меньше обеспокоены эффектами насыщения электронами, хотя это оспаривается. С другой стороны, датчики скрытого монтажа, будучи частью стены, вызывают меньше возмущений. Знание угла поля необходимо при использовании гордых датчиков для определения потоков на стенку, а при использовании датчиков скрытого монтажа — для определения плотности.

В очень горячей и плотной плазме, как обнаружено в исследованиях термоядерного синтеза, часто необходимо ограничить тепловую нагрузку на зонд, ограничив время воздействия. установлен Возвратно-поступательный зонд на рычаге, который перемещается в плазму и обратно, обычно примерно за одну секунду, с помощью либо пневматического привода, либо электромагнитного привода с использованием окружающего магнитного поля. Выдвижные зонды аналогичны, но электроды находятся за экраном и перемещаются лишь на несколько миллиметров, необходимых для попадания их в плазму возле стены.

Зонд Ленгмюра можно приобрести в готовом виде примерно за 15 000 долларов США или его может изготовить опытный исследователь или техник. При работе на частотах ниже 100 МГц рекомендуется использовать блокирующие фильтры и принять необходимые меры по заземлению.

В низкотемпературной плазме, в которой зонд не нагревается, загрязнение поверхности может стать проблемой. Этот эффект может вызвать гистерезис ВАХ и ограничить ток, собираемый датчиком. Для очистки зонда и предотвращения ошибочных результатов можно использовать нагревательный механизм или плазму тлеющего разряда.

См. также

• Двойной сегментный зонд Ленгмюра
• Параметры плазмы

Дальнейшее чтение

• Хопвуд, Дж. (1993). «Ленгмюровские зондовые измерения радиочастотной индукционной плазмы». Журнал вакуумной науки и техники А. 11 (1): 152–156. Бибкод : 1993JVST...11..152H . дои : 10.1116/1.578282 .
• А. Швабедиссен; ЕС Бенк; Дж. Р. Робертс (1997). «Измерения с помощью ленгмюровского зонда в источнике индуктивно связанной плазмы» . Физ. Преподобный Е. 55 (3): 3450–3459. Бибкод : 1997PhRvE..55.3450S . дои : 10.1103/PhysRevE.55.3450 .

Внешние ссылки

• Заметки по теории и конструкции зонда Ленгмюра Ф. Ф. Чена