Поток Куэтта

В гидродинамике в пространстве между двумя поверхностями , течение Куэтта — это течение вязкой жидкости одна из которых движется по касательной относительно другой. Относительное движение поверхностей создает напряжение сдвига в жидкости и вызывает течение. В зависимости от определения термина может также существовать приложенный градиент давления в направлении потока .

Конфигурация Куэтта моделирует некоторые практические проблемы, такие как Земли мантия и атмосфера . и течь в слегка нагруженных подшипниках скольжения . Он также используется в вискозиметрии и для демонстрации приближений обратимости .

Он назван в честь Мориса Куэтта , профессора физики Французского университета Анжера в конце 19 века.

Одеяло с плоским потоком

Простая конфигурация Куэтта с использованием двух бесконечных плоских пластин.

Течение Куэтта часто используется на курсах бакалавриата по физике и инженерному делу для иллюстрации движения жидкости , вызванного сдвигом . Простая конфигурация соответствует двум бесконечным параллельным пластинам, разделенным расстоянием $h$; одна пластина перемещается с постоянной относительной скоростью $U$ в своей плоскости. Если пренебречь градиентами давления, уравнения Навье – Стокса упрощаются до

${\frac {d^{2}u}{dy^{2}}}=0,$

где $y$ – пространственная координата, нормальная к пластинам, а $u(y)$ – поле скоростей. Это уравнение отражает предположение, что поток однонаправленный , то есть только одна из трех составляющих скорости. $(u,v,w)$ является нетривиальным. Если нижняя пластина соответствует $y=0$, граничные условия $u(0)=0$ и $u(h)=U$. Точное решение

$u(y)=U{\frac {y}{h}}$

можно найти путем двукратного интегрирования и решения констант с использованием граничных условий.Примечательным аспектом течения является то, что напряжение сдвига является постоянным во всей области. В частности, первая производная скорости $U/h$, является постоянным. Согласно закону вязкости Ньютона ( ньютоновская жидкость ), напряжение сдвига является произведением этого выражения и (постоянной) вязкости жидкости .

Запускать

Схема запуска Куэтта

В действительности решение Куэтта не достигается мгновенно. «Проблема запуска», описывающая подход к устойчивому состоянию, определяется выражением

${\frac {\partial u}{\partial t}}=\nu {\frac {\partial ^{2}u}{\partial y^{2}}}$

при условии начального состояния

$u(y,0)=0,\quad 0<y<h,$

и с теми же граничными условиями, что и установившийся поток:

$u(0,t)=0,\quad u(h,t)=U,\quad t>0.$

Задачу можно сделать однородной, вычитая устойчивое решение. Тогда применение разделения переменных приводит к решению:

$u(y,t)=U{\frac {y}{h}}-{\frac {2U}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{n}}e^{-n^{2}\pi ^{2}{\frac {\nu t}{h^{2}}}}\sin \left[n\pi \left(1-{\frac {y}{h}}\right)\right]$.

Временная шкала, описывающая релаксацию до установившегося состояния, равна $t\sim h^{2}/\nu$, как показано на рисунке. Время, необходимое для достижения установившегося состояния, зависит только от расстояния между пластинами. $h$ и кинематическая вязкость жидкости, но не на $U$.

Плоское течение с градиентом давления

Более общий поток Куэтта включает постоянный градиент давления. $G=-dp/dx=\mathrm {constant}$ в направлении, параллельном пластинам. Уравнения Навье – Стокса имеют вид

${\frac {d^{2}u}{dy^{2}}}=-{\frac {G}{\mu }},$

где $\mu$ – динамическая вязкость . Дважды интегрирование приведенного выше уравнения и применение граничных условий (таких же, как в случае течения Куэтта без градиента давления) дает

$u(y)={\frac {G}{2\mu }}y\,(h-y)+U{\frac {y}{h}}.$

Градиент давления может быть положительным (неблагоприятный градиент давления) или отрицательным (благоприятный градиент давления). В предельном случае неподвижных пластин ( $U=0$), поток называется плоским потоком Пуазейля и имеет симметричный (относительно горизонтальной средней плоскости) параболический профиль скорости.

Сжимаемый поток

Сжимаемый поток Куэтта для $\mathrm {M} =0$

Сжимаемый поток Куэтта для $\mathrm {M} ^{2}\mathrm {Pr} =7.5$

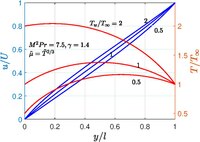
В несжимаемом потоке профиль скорости линейный, поскольку температура жидкости постоянна. Когда верхняя и нижняя стенки поддерживаются при разных температурах, профиль скорости усложняется. Однако у него есть точное неявное решение, как показал Ч. Р. Иллингворт в 1950 году.

Рассмотрим плоское течение Куэтта с покоящейся нижней стенкой и движущейся с постоянной скоростью верхней стенкой. $U$. Обозначим свойства жидкости у нижней стенки индексом $w$ и свойства на верхней стене с индексом $\infty$. Свойства и давление у верхней стенки заданы и приняты за справочные величины. Позволять $l$ быть расстоянием между двумя стенами. Граничные условия:

$u=0,\ v=0,\ h=h_{w}=c_{pw}T_{w}\ {\text{at}}\ y=0,$

$u=U,\ v=0,\ h=h_{\infty }=c_{p\infty }T_{\infty },\ p=p_{\infty }\ {\text{at}}\ y=l$

где $h$ удельная энтальпия и $c_{p}$ это удельная теплоемкость . Сохранение массы и $y$- импульс требует $v=0,\ p=p_{\infty }$ повсюду в области потока. Сохранение энергии и $x$-импульс уменьшиться до

${\frac {d}{dy}}\left(\mu {\frac {du}{dy}}\right)=0,\quad \Rightarrow \quad {\frac {d\tau }{dy}}=0,\quad \Rightarrow \quad \tau =\tau _{w}$

${\frac {1}{\mathrm {Pr} }}{\frac {d}{dy}}\left(\mu {\frac {dh}{dy}}\right)+\mu \left({\frac {du}{dy}}\right)^{2}=0.$

где $\tau =\tau _{w}={\text{constant}}$ – напряжение сдвига стенки. Течение не зависит от числа Рейнольдса. $\mathrm {Re} =Ul/\nu _{\infty }$, а скорее по числу Прандтля $\mathrm {Pr} =\mu _{\infty }c_{p\infty }/\kappa _{\infty }$ и число Маха $\mathrm {M} =U/c_{\infty }=U/{\sqrt {(\gamma -1)h_{\infty }}}$, где $\kappa$ - теплопроводность , $c$ это скорость звука и $\gamma$ это коэффициент удельной теплоемкости . Введем безразмерные переменные

${\tilde {y}}={\frac {y}{l}},\quad {\tilde {T}}={\frac {T}{T_{\infty }}},\quad {\tilde {T}}_{w}={\frac {T_{w}}{T_{\infty }}},\quad {\tilde {h}}={\frac {h}{h_{\infty }}},\quad {\tilde {h}}_{w}={\frac {h_{w}}{h_{\infty }}},\quad {\tilde {u}}={\frac {u}{U}},\quad {\tilde {\mu }}={\frac {\mu }{\mu _{\infty }}},\quad {\tilde {\tau }}_{w}={\frac {\tau _{w}}{\mu _{\infty }U/l}}$

В этих величинах решения имеют вид

${\tilde {h}}={\tilde {h}}_{w}+\left[{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} +(1-{\tilde {h}}_{w})\right]{\tilde {u}}-{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} \,{\tilde {u}}^{2},$

${\tilde {y}}={\frac {1}{{\tilde {\tau }}_{w}}}\int _{0}^{\tilde {u}}{\tilde {\mu }}\,d{\tilde {u}},\quad {\tilde {\tau }}_{w}=\int _{0}^{1}{\tilde {\mu }}\,d{\tilde {u}},\quad q_{w}=-{\frac {1}{\mathrm {Pr} }}\tau _{w}\left({\frac {dh}{du}}\right)_{w},$

где $q_{w}$ – тепло, передаваемое в единицу времени на единицу площади от нижней стенки. Таким образом ${\tilde {h}},{\tilde {T}},{\tilde {u}},{\tilde {\mu }}$ являются неявными функциями $y$. Решение также можно записать через температуру восстановления. $T_{r}$ и энтальпия восстановления $h_{r}$ оцениваются при температуре изолированной стены, т.е. значения $T_{w}$ и $h_{w}$ для чего $q_{w}=0$. Тогда решение

${\frac {q_{w}}{\tau _{w}U}}={\frac {{\tilde {T}}_{w}-{\tilde {T}}_{r}}{(\gamma -1)\mathrm {M} ^{2}\mathrm {Pr} }},\quad {\tilde {T}}_{r}=1+{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} ,$

${\tilde {h}}={\tilde {h}}_{w}+({\tilde {h}}_{r}-{\tilde {h}}_{w}){\tilde {u}}-{\frac {\gamma -1}{2}}\mathrm {M} ^{2}\mathrm {Pr} \,{\tilde {u}}^{2}.$

Если удельная теплоемкость постоянна, то ${\tilde {h}}={\tilde {T}}$. Когда $\mathrm {M} \rightarrow 0$ и $T_{w}=T_{\infty },\Rightarrow q_{w}=0$, затем $T$ и $\mu$ всюду постоянны, что восстанавливает решение течения Куэтта несжимаемой жидкости. В противном случае необходимо знать полную температурную зависимость ${\tilde {\mu }}({\tilde {T}})$. Хотя не существует простого выражения для ${\tilde {\mu }}({\tilde {T}})$ это одновременно и точно, и в целом, для некоторых материалов существует несколько приближений — см., например, температурную зависимость вязкости . Когда $\mathrm {M} \rightarrow 0$ и $q_{w}\neq 0$, восстановительные величины становятся единицей ${\tilde {T}}_{r}=1$. Для воздуха значения $\gamma =1.4,\ {\tilde {\mu }}({\tilde {T}})={\tilde {T}}^{2/3}$ широко используются, и результаты для этого случая показаны на рисунке.

Эффекты диссоциации и ионизации (т.е. $c_{p}$ не является постоянной) также изучались; в этом случае температура восстановления снижается из-за диссоциации молекул.

Прямоугольный канал

Течение Куэтта для квадратного канала

Течение Куэтта с h/l=0,1

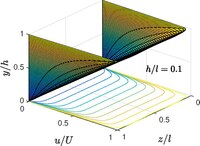
Одномерный поток $u(y)$ справедливо, когда обе пластины имеют бесконечную длину в продольном направлении ( $x$) и по размаху ( $z$) направления. Когда длина по размаху конечна, поток становится двумерным и $u$ является функцией обоих $y$ и $z$. Однако бесконечную длину в продольном направлении необходимо сохранить, чтобы обеспечить однонаправленный характер потока.

В качестве примера рассмотрим бесконечно длинный прямоугольный канал с поперечной высотой $h$ и ширина по размаху $l$, при условии, что верхняя стенка движется с постоянной скоростью $U$. Без наложенного градиента давления уравнения Навье – Стокса сводятся к

${\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}=0$

с граничными условиями

$u(0,z)=0,\quad u(h,z)=U,$

$u(y,0)=0,\quad u(y,l)=0.$

Используя разделение переменных , решение дается формулой

$u(y,z)={\frac {4U}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}{\frac {\sinh(\beta _{n}y)}{\sinh(\beta _{n}h)}}\sin(\beta _{n}z),\quad \beta _{n}={\frac {(2n-1)\pi }{l}}.$

Когда $h/l\ll 1$, плоское течение Куэтта восстанавливается, как показано на рисунке.

Коаксиальные цилиндры

Течение Тейлора – Куэтта представляет собой течение между двумя вращающимися коаксиальными цилиндрами бесконечной длины. Исходная задача была решена Стоуксом в 1845 году. но имя Джеффри Ингрэма Тейлора было связано с потоком, потому что он изучал его устойчивость в знаменитой статье 1923 года.

Задача может быть решена в цилиндрических координатах $(r,\theta ,z)$. Обозначим радиусы внутреннего и внешнего цилиндров как $R_{1}$ и $R_{2}$. Предполагая, что цилиндры вращаются с постоянными угловыми скоростями. $\Omega _{1}$ и $\Omega _{2}$, то скорость в $\theta$-направление

$v_{\theta }(r)=ar+{\frac {b}{r}},\qquad a={\frac {\Omega _{2}R_{2}^{2}-\Omega _{1}R_{1}^{2}}{R_{2}^{2}-R_{1}^{2}}},\quad b={\frac {(\Omega _{1}-\Omega _{2})R_{1}^{2}R_{2}^{2}}{R_{2}^{2}-R_{1}^{2}}}.$

Это уравнение показывает, что эффекты кривизны больше не допускают постоянного сдвига в области потока.

Коаксиальные цилиндры конечной длины

Классическая задача Тейлора – Куэтта предполагает наличие бесконечно длинных цилиндров; если цилиндры имеют немаловажную конечную длину $l$, то анализ необходимо изменить (хотя поток по-прежнему однонаправленный). Для $\Omega _{2}=0$, проблема конечной длины может быть решена с использованием разделения переменных или интегральных преобразований , что дает:

$v_{\theta }(r,z)={\frac {4R_{1}\Omega _{1}}{\pi }}\sum _{n=1}^{\infty }{\frac {1}{2n-1}}{\frac {I_{1}(\beta _{n}R_{2})K_{1}(\beta _{n}r)-K_{1}(\beta _{n}R_{2})I_{1}(\beta _{n}r)}{I_{1}(\beta _{n}R_{2})K_{1}(\beta _{n}R_{1})-K_{1}(\beta _{n}R_{2})I_{1}(\beta _{n}R_{1})}}\sin(\beta _{n}z),\quad \beta _{n}={\frac {(2n-1)\pi }{l}},$

где $I(\beta _{n}r),\ K(\beta _{n}r)$ – модифицированные функции Бесселя первого и второго рода.

См. также

• Ламинарный поток
• Течение Стокса-Куэтта
• Уравнение Хагена – Пуазейля
• Поток Тейлора – Куэтта
• Поток Хагена–Пуазейля из уравнений Навье–Стокса

Источники

• Ачесон, диджей (1990). Элементарная гидродинамика . Издательство Оксфордского университета. ISBN  0-19-859679-0 .
• Бэтчелор, ГК (2000) [1967]. Введение в гидродинамику . Издательство Кембриджского университета. ISBN  0-521-66396-2 .
• Гийон, Этьен; Юлен, Жан-Пьер; Пети, Люк; Митеску, Каталин Д. (2001). Физическая гидродинамика . Издательство Оксфордского университета. ISBN  0-19-851746-7 .
• Хеллер, Джон П. (1960). «Несмешиваемая демонстрация». Американский журнал физики . 28 (4): 348–353. Бибкод : 1960AmJPh..28..348H . дои : 10.1119/1.1935802 . ISSN   0002-9505 .
• Иллингворт, ЧР (1950). «Некоторые решения уравнений течения вязкой сжимаемой жидкости». Математические труды Кембриджского философского общества . 46 (3): 469–478. Бибкод : 1950PCPS...46..469I . дои : 10.1017/S0305004100025986 . ISSN   0305-0041 . S2CID   122559614 .
• Кунду, Пиджуш К.; Коэн, Ира М.; Даулинг, Дэвид Р. (2016). Механика жидкости (6-е изд.). Эльзевир. ISBN  978-0-12-405935-1 .
• Лагерстрем, Пако (1996). Теория ламинарного течения . Издательство Принстонского университета. ISBN  978-0691025988 .
• Ландау, Л.Д.; Лифшиц, Э.М. (1987). Механика жидкости (2-е изд.). Эльзевир. ISBN  978-0-08-057073-0 .
• Липманн, Х.В. и З.О. Блевисс. «Влияние диссоциации и ионизации на сжимаемый поток Куэтта». Представитель Douglas Aircraft Co. СМ-19831 130 (1956 г.).
• Липманн, Ганс Вольфганг и Анатол Рошко . Элементы газодинамики. Курьерская корпорация, 1957 год.
• Позрикидис, К. (2011). Введение в теоретическую и вычислительную гидродинамику . Издательство Оксфордского университета. ISBN  978-0-19-975207-2 .
• Ричард Фейнман (1964) Лекции Фейнмана по физике: в основном электромагнетизм и материя , § 41–6 Поток Куэтта , Аддисон – Уэсли ISBN   0-201-02117-X
• Стоукс, Джордж Габриэль (1880). «К теориям внутреннего трения движущихся жидкостей, а также равновесия и движения упругих твердых тел» . Математические и физические статьи . Издательство Кембриджского университета: 75–129. дои : 10.1017/CBO9780511702242.005 . ISBN  9780511702242 .
• Тейлор, Джеффри И. (1923). «Устойчивость вязкой жидкости, находящейся между двумя вращающимися цилиндрами» . Философские труды Лондонского королевского общества . Серия А, содержащая статьи математического или физического характера. 223 (605–615): 289–343. Бибкод : 1923RSPTA.223..289T . дои : 10.1098/rsta.1923.0008 . JSTOR   91148 .
• Вендл, Майкл К. (1999). «Общее решение профиля потока Куэтта». Физический обзор E . 60 (5): 6192–6194. Бибкод : 1999PhRvE..60.6192W . дои : 10.1103/PhysRevE.60.6192 . ISSN   1063-651X . ПМИД   11970531 .
• Жиленко Дмитрий Владимирович; Кривоносова Ольга; Грицевич, Мария; Прочтите, Питер (2018). «Выбор волнового числа при наличии шума: результаты эксперимента». Хаос: междисциплинарный журнал нелинейной науки . 28 (5): 053110. Бибкод : 2018Хаос..28e3110Z . дои : 10.1063/1.5011349 . hdl : 10138/240787 . ISSN   1054-1500 . ПМИД   29857673 . S2CID   46925417 .

Внешние ссылки

• Глоссарий AMS: течение Куэтта
• Взгляд реологов: наука, лежащая в основе аксессуара ячейки Куэтта