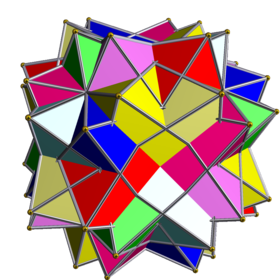
Соединение восьми октаэдров со свободой вращения.

Соединение восьми октаэдров со свободой вращения.
Тип	Однородный состав
Индекс	УК 11
Многогранники	8 октаэдров
Лица	16+48 треугольников
Края	96
Вершины	48
Группа симметрии	октаэдрический ( о ч )
Подгруппа, ограничивающаяся одним компонентом	6-кратное неправильное вращение ( S 6 )

Соединение восьми октаэдров со свободой вращения представляет собой соединение однородного многогранника . Он состоит из симметричного расположения 8 октаэдров , рассматриваемых как треугольные антипризмы . Его можно построить, наложив друг на друга восемь одинаковых октаэдров, а затем попарно вращая их вокруг четырех осей, проходящих через центры двух противоположных октаэдрических граней. Каждый октаэдр повернут на равный (и противоположный в пределах пары) угол θ .

Его можно построить путем наложения двух соединений из четырех октаэдров со свободой вращения : одного с вращением θ , а другого с вращением − θ .

При θ = 0 все восемь октаэдров совпадают. Когда θ равен 60 градусам, октаэдры совпадают попарно, образуя (две наложенные копии) соединение четырех октаэдров .

Декартовы координаты

Декартовы координаты вершин этого соединения — это все перестановки

$(\pm (1-\cos(\theta )+{\sqrt {3}}\sin(\theta )),\pm (1-\cos(\theta )-{\sqrt {3}}\sin(\theta )),\pm (1+2\cos(\theta ))).$

Галерея

• Соединения восьми октаэдров со свободой вращения
• 
  θ = 0°
• 
  θ = 5°
• 
  θ = 10°
• 
  θ = 15°
• 
  θ = 20°
• 
  θ = 25°
• 
  θ = 30°
• 
  θ = 35°
• 
  θ = 40°
• 
  θ = 45°
• 
  θ = 50°
• 
  θ = 55°
• 
  θ = 60°

Ссылки

• Скиллинг, Джон (1976), «Однородные соединения однородных многогранников», Mathematical Proceedings of the Cambridge Philosophical Society , 79 (3): 447–457, doi : 10.1017/S0305004100052440 , MR   0397554 .